Ramping of Heat Loads and Convection Conditions
In transient thermal analysis, Creo Simulate turns on any heat load or convection condition that is not equal to zero at the start of the analysis. Because its algorithm is adaptive, Creo Simulate sets the p-order to its maximum possible value to capture the instantaneous change in heat load or convection condition.
The algorithm is more efficient if all heat loads and convection conditions are ramped from zero to their final value over some short period of time. You can use the mesh parameters and the material properties discussed below to estimate the time.
The finite element method is only able to capture time scales of the order of
where
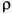
is the density,
c is the specific heat,
k is the conductivity,
L is the largest length scale of an element, and
p is the p-order. Any time scale that is smaller than this causes errors. For example, if you enter a time-dependent heat load or bulk temperature that is a sine wave with a period much smaller than this value, the solution would have a large error. Therefore any ramp function must use a period at least as large as the local value of

computed for the elements adjacent to the heat load or convection condition.
A convection condition having a large Biot number can create a thin layer with large temperature gradients that is smaller than Creo Simulate can represent accurately. Creo Simulate defines the Biot number by
where
h is the convective heat transfer coefficient (also called film coefficient in
Creo Simulate),
k is the conductivity, and
L is the largest length scale of an element. If the Biot number is much greater than 1, the solution can have a large error. You can reduce the error in the solution by ramping the bulk temperature from the initial condition of the model to its final value over a period of time larger than

. You can use the local value of

for the elements adjacent to the convection condition and in many cases get accurate results, as mentioned above.
To model a time-dependent prescribed temperature, you can enter a convection condition with a large value of
h and set the bulk temperature as a function of time equal to the desired prescribed temperature. A Biot number of 100 should be sufficient. The bulk temperature should not vary more rapidly than

in order to avoid errors in the solution.
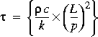
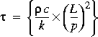
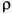 is the density, c is the specific heat, k is the conductivity, L is the largest length scale of an element, and p is the p-order. Any time scale that is smaller than this causes errors. For example, if you enter a time-dependent heat load or bulk temperature that is a sine wave with a period much smaller than this value, the solution would have a large error. Therefore any ramp function must use a period at least as large as the local value of
is the density, c is the specific heat, k is the conductivity, L is the largest length scale of an element, and p is the p-order. Any time scale that is smaller than this causes errors. For example, if you enter a time-dependent heat load or bulk temperature that is a sine wave with a period much smaller than this value, the solution would have a large error. Therefore any ramp function must use a period at least as large as the local value of  computed for the elements adjacent to the heat load or convection condition.
computed for the elements adjacent to the heat load or convection condition.
 . You can use the local value of
. You can use the local value of  for the elements adjacent to the convection condition and in many cases get accurate results, as mentioned above.
for the elements adjacent to the convection condition and in many cases get accurate results, as mentioned above. in order to avoid errors in the solution.
in order to avoid errors in the solution.