Static Analysis Problems
This chapter contains static analysis problems and the results of structural analyses. In a Static analysis, Creo Simulate calculates deformations, stresses, and strains on your model in response to specified loads and subject to specified constraints. It also automatically calculates all predefined measures. This list of measures differs based on the analysis type.
|
|
Note that displacement values are always absolute values.
|
This chapter contains the following models:
mvss001: 2D Axisymmetric Cylindrical Shell
|
Analysis Type:
|
Static
|
|
Model Type:
|
2D Axisymmetric
|
|
Comparison:
|
NASTRAN No. V2411
|
|
Reference:
|
• P.E. Grafton and D.R. Strome, "Analysis of Axisymmetrical Shells by the Direct Stiffness Method," AIAA Journal, 1(10): 2342-2347.
• J.W. Jones and H.H. Fong, "Evaluation of NASTRAN," Structural Mechanics Software Series, Vol. IV (N. Perrone and W. Pilkey, eds.), 1982.
|
|
Description:
|
Find the radial deflection at the loaded end of a cantilever cylinder that is modeled axisymmetrically.
|

Element B is optional, but has been included here to increase the accuracy of results in the area local to the loaded end and to reduce computation time. |
Specifications
Element Type: | 2D shell (2) | |
Units: | IPS | |
Dimensions: | length: 6 radius: 5 thickness: 0.01 | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 1e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on point A: fixed in all DOF | |
Load: | placed on point C: FX = 1 Distribution: N/A Spatial Variation: N/A | |
Comparison of Results Data
Theory | MSC/ NASTRAN | Structure | % Difference | |
|---|---|---|---|---|
Radial Deflection @ Load (a=disp_x_radial) | 2.8769e-3 | 2.8715e-3 | 2.8725e-3 | 0.15% |
Convergence %: 0.5% on Local Disp and SE | Max P: 7 | No. Equations: 33 | ||
mvss002: 2D Axisymmetric Flat Circular Plate
Analysis Type: | Static |
Model Type: | 2D Axisymmetric |
Comparison: | ANSYS No. 15 |
Reference: | Timoshenko, S. Strength of Materials, Part II, Advanced Theory and Problems. 3rd ed. NY: D. Van Nostrand Co., Inc. 1956, pp. 96, 97, and 103. |
Description: | A flat circular plate, modeled axisymmetrically, is subjected to various edge constraints and surface loadings. Determine the maximum stress for each case. |

Specifications
Element Type: | 2D shell (1) | |
Units: | IPS | |
Dimensions: | radius: 40 thickness: 1 | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | Location | Degrees of Freedom |
|---|---|---|
clamped | placed on point B: | fixed in all DOF |
simple | placed on point B: | fixed in TransX and TransY |
Loads: | Location/Magnitude: | Distribution: | Spatial Variation: |
|---|---|---|---|
clamped | placed on edge A-B: FY = 6 | per unit area | uniform |
simple | placed on edge A-B: FY = 1.5 | per unit area | uniform |
Comparison of Results Data
Theory | ANSYS | Structure | % Difference | |
|---|---|---|---|---|
Maximum Stress (m=max_prin_mag, a=clamped) | 7200 | 7152 | 7200 | 0.0% |
Convergence %: 0.0% on Local Disp and SE | Max P: 5 | No. Equations: 15 | ||
Maximum Stress (m=max_prin_mag, a=simple) | 2970 | 2989 | 29701 | 0.0% |
Convergence %: 0.0% on Local Disp and SE | Max P: 5 | No. Equations: 16 | ||
1 Sign of result is dependent upon direction of load.
mvss003: 2D Plane Stress Cantilever Plate
Analysis Type: | Static |
Model Type: | 2D Plane Stress |
Comparison: | NASTRAN No. V2408A |
Reference: | Singer, Ferdinand L. Strength of Materials. Harper & Row, 1962, Art. 52, p. 133. |
Description: | Find the bending stress at the fixed end for a cantilever plate subjected to an in-plane shear load. |

Specifications
Element Type: | 2D plate (1) | |
Units: | IPS | |
Dimensions: | length: 3 height: 0.6 thickness: 0.1 | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 1.07e7 | Poisson's Ratio: 0 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on edge A-B: fixed in TransX, TransY | |
Loads: | placed on edge C-D: FY= –200 Distribution: per unit length Spatial Variation: uniform | |
The theoretical results are based on elementary beam theory. Structure models the actual physical structure, capturing the singular stresses present at the constrained corners. Setting Poisson's ratio equal to zero reduces the model to its elementary form. | ||
Comparison of Results Data
Theory | MSC/ NASTRAN | Structure | % Difference | |
|---|---|---|---|---|
Bending Stress @ Node A (m=max_stress_xx) | 6.0e4 | 5.5190e4 | 6.0121e4 | 0.20% |
Convergence %: 0.0% on Local Disp and SE | Max P: 4 | No. Equations: 22 | ||
mvss004: 2D Plane Strain Thick-Walled Cylinder
Analysis Type: | Static |
Model Type: | 2D Plane Strain |
Comparison: | The MacNealHarder Accuracy Tests |
Reference: | MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Description: | A thick-walled cylinder, modeled symmetrically, is loaded with unit internal pressure. Find the radial displacement at the inner radius for two nearly incompressible materials. |

Specifications
Element Type: | 2D solid (1) | |
Units: | IPS | |
Dimensions: | outer radius: 9.0 inner radius: 3.0 | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 1000 | Poisson's Ratio: • 0.49 (case 1) • 0.499 (case 2) |
Constraints (UCS): | placed on edges A-B & C-D: fixed in all DOF except TransR | |
Loads: | placed on edge A-D: pressure load = 1 Distribution: N/A Spatial Variation: uniform | |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Radial Displacement @ Inner Radius (case 1) (m=rad_disp) | 5.0399e-3 | 5.0394e-3 | <0.01% |
Convergence %:1% on Local Disp and SE | Max P: 6 | No. Equations: 38 | |
Radial Displacement @ Inner Radius (case 2) (m=rad_disp) | 5.0602e-3 | 5.0553e-3 | 0.09% |
Convergence %: 1.0% on Local Disp and SE | Max P: 6 | No. Equations: 38 | |
mvss005: 2D Axisymmetric Thick-Walled Cylinder
Analysis Type: | Static |
Model Type: | 2D Axisymmetric |
Comparison: | NASTRAN No. V2410 |
Reference: | Crandall S.H., Dahl N.C. , and Larnder T.J. An Introduction to the Mechanics of Solids. 2nd ed. NY: McGraw-Hill Book Co., 1972, pp. 293-297. |
Description: | Find the stress at radii r = 6.5" and r = 11.5". A thick-walled cylinder is modeled axisymmetrically and subjected to internal pressure. |

Specifications
Element Type: | 2D solid (3) | |
Units: | IPS | |
Dimensions: | inner radius: 6 height: 8 thickness: 6 | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0 Thermal Expansion: 0 Conductivity: 0 |
Constraints (UCS): | placed on edges A-D & B-C: fixed in TransY and RotZ | |
Loads: | placed on edge A-B: pressure load = 10 Distribution: per unit area Spatial Variation: uniform | |
Comparison of Results Data
Theory | MSC/ NASTRAN | Structure | % Difference | ||
|---|---|---|---|---|---|
@ r = 6.5 | Stress Radial (m=r6_5_radial) | -8.03 | -8.05 | -7.9720 | 0.72% |
Stress Hoop (m=r6_5_hoop) | 14.69 | 14.73 | 14.69 | 0.0% | |
@ r = 11.5 | Stress Radial (m=r11_5_radial) | -0.30 | -0.30 | -2.6636e-1 | 0.0% |
Stress Hoop (m=r11_5_hoop) | 6.96 | 6.96 | 6.96 | 0.0% | |
Convergence %: 0.25% on Local Disp and SE | Max P: 4 | No. Equations: 54 | |||
mvss006: 3D Cantilever Beam
Analysis Type: | Static |
Model Type: | 3D |
Comparison: | NASTRAN No. V2405 |
Reference: | Roark, R.J., and Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Book Co., 1982, p. 96. |
Description: | A cantilever beam is subjected to a load at the free end. Find the deflection at the free end and the bending stress at the fixed end. |

Specifications
Element Type: | beam (1) | |
Units: | IPS | |
Dimensions: | length: 30 | |
Beam Properties: | Area: 0.310 IYY: 0.0241 Shear FY: 1000 1 CY: 0.5 | J: 0.0631 IZZ: 0.0390 Shear FZ: 1000 1 CZ: 0.375 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 1.0e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF | |
Loads: | placed on point B: FY = 100 Distribution: N/A Spatial Variation: N/A | |
1 Structure beams consider shear; however, the represented theoretical problem does not. The values for shear factor compensate for this.
Comparison of Results Data
Theory | MSC/ NASTRAN | Structure | % Difference | |
Deflection @ Tip (m=max_disp_y) | 2.3077 | 2.3077 | 2.3094 | 0.073% |
Bending Stress @ Fixed End (m=max_beam_bending) | 38461 | 38461 | 38461 | 0.0% |
Convergence %: 0.0% on Local Disp and SE | Max P: 4 | No. Equations: 24 | ||
mvss007: 3D Beam with Multiple Constraints
Analysis Type: | Static |
Model Type: | 3D |
Comparison: | ANSYS No. 2 |
Reference: | Timoshenko, S. Strength of Materials, Part I, Elementary Theory and Problems. 3rd ed. NY: D. Van Nostrand Co., Inc., 1955, p. 98, Problem 4. |
Description: | A standard 30" WF beam, supported as shown below, is loaded on the overhangs uniformly. Find the maximum bending stress and deflection at the middle of the beam. |

Specifications
Element Type: | beam (4) | |
Units: | IPS | |
Dimensions: | length: 480 | |
Beam Properties: | Area: 50.65 IYY: 1 Shear FY: 0.8333 CY: 15 | J: 7893 IZZ: 7892 Shear FZ: 0.8333 CZ: 15 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints | Location | Degrees of Freedom |
|---|---|---|
placed on point B: placed on point D: | fixed in all DOF except RotY and RotZ fixed in TransY and TransZ |
Loads | Location/Magnitude | Distribution | Spatial Variation |
|---|---|---|---|
placed on edge A-B: FY = 833.33 placed on edge D-E: FY = 833.33 | per unit length per unit length | uniform uniform |
Comparison of Results Data
Theory | ANSYS | Structure | % Difference | |
|---|---|---|---|---|
Max Bending Stress @ Middle (m=max_beam_bending) | 11400 | 11404 | 11403.91 | 0.03% |
Max Deflection @ Middle (m=disp_center) | 0.182 | 0.182 | 0.182 | 0.0% |
Convergence %: 0.0% on Local Disp and SE | Max P: 4 | No. Equations: 96 | ||
mvss008: 3D Beam with Parallelogram-Shaped Shell Elements
Analysis Type: | Static |
Model Type: | 3D |
Comparison: | The MacNealHarder Accuracy Tests |
Reference: | MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Description: | A straight cantilever beam, constructed of parallelogram-shaped elements, is subjected to four different unit loads at the free end, including • extension • in-plane shear • out-of-plane shear • twisting loads Find the tip displacement in the direction of the load for each case. |

Specifications
Element Type: | shell (3) | |
Units: | IPS | |
Dimensions: | length: 6 width: 0.2 thickness: 0.1 | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 1e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on edge A-D: fixed in all DOF | |
Loads: | Location/Magnitude: | Distribution: | Spatial Variation: |
|---|---|---|---|
extension | placed on edge B-C: FX = 1 | total load | uniform |
in_plane | placed on edge B-C: FY = 1 | total load | uniform |
out_plane | placed on edge B-C: FZ = 1 | total load | uniform |
twist | placed on point E: MX = 1 | total load | N/A |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Tip Disp. in Direction of Load (l=extension, m=max_disp_x) | 3e-5 | 2.998e-5 | 0.06% |
Tip Disp. in Direction of Load (l=in_plane, m=max_disp_y) | 0.1081 | 0.1078 | 0.27% |
Tip Disp. in Direction of Load (l=out_plane, m=max_disp_z) | 0.4321 | 0.4309 | 0.27% |
Tip Disp. in Direction of Load (l=twist, m=max_rot_x) | 0.03408 1 | 0.03424 | 0.46% |
Convergence %: 0.9% on Local Disp and SE | Max P: 6 | No. Equations: 396 | |
1 There is a typographical error in Table 3 (p. 10) of MacNeal-Harder for the twist load on a straight beam. It should read 0.03408.
mvss009: 3D Beam with Trapezoidal-Shaped Shell Elements
Analysis Type: | Static |
Model Type: | 3D |
Comparison: | The MacNealHarder Accuracy Tests |
Reference: | MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Description: | A straight cantilever beam, constructed of trapezoidal-shaped elements, is subjected to four different unit loads at the free end, including • extension • in-plane shear • out-of-plane shear • twisting Find the tip displacement in the direction of the load for each case. |
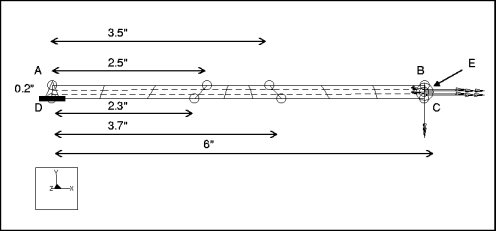
Specifications
Element Type: | shell (3) | |
Units: | IPS | |
Dimensions: | length: 6 width: 0.2 thickness: 0.1 | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 1e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on edge A-D: fixed in all DOF | |
Loads: | Location/Magnitude: | Distribution: | Spatial Variation: |
|---|---|---|---|
extension | placed on edge B-C: FX = 1 | total load | uniform |
in_plane | placed on edge B-C: FY = 1 | total load | uniform |
out_plane | placed on edge B-C: FZ = 1 | total load | uniform |
twist | placed on point E: MX = 1 | total load | N/A |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Tip Disp. in Direction of Load (l=extension, m=max_disp_x) | 3e-5 | 2.998e-5 | 0.08% |
Tip Disp. in Direction of Load (l=in_plane, m=max_disp_y) | 0.1081 | 0.1079 | 0.32% |
Tip Disp. in Direction of Load (l=out_plane, m=max_disp_z) | 0.4321 | .4311 | 0.23% |
Tip Disp. in Direction of Load (l=twist, m=max_rot_x) | 0.03408 1 | 0.03381 | 0.79% |
Convergence %: 0.7% on Local Disp and SE | Max P: 6 | No. Equations: 906 | |
1 There is a typographical error in Table 3 (p. 10) of the McNeal-Harder reference for the twist load on a straight beam. It should read 0.03408.
mvss010: 3D Curved Beam Modeled with Shells
Analysis Type: | Static |
Model Type: | 3D |
Comparison: | The MacNealHarder Accuracy Tests |
Reference: | MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Description: | A curved beam, spanning a 90  arc, is fixed at one end and free at the other. If the beam is subjected to in-plane and out-of-plane loads at the free end, find the tip displacement in the direction of the load for both cases. arc, is fixed at one end and free at the other. If the beam is subjected to in-plane and out-of-plane loads at the free end, find the tip displacement in the direction of the load for both cases. |

Specifications
Element Type: | shell (2) | |
Units: | IPS | |
Dimensions: | outer radius: 4.32 inner radius: 4.12 thickness: 0.1 | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 1e7 | Poisson's Ratio: 0.25 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on edge A-D: fixed in all DOF | |
Loads: | Location/Magnitude: | Distribution: | Spatial Variation: |
|---|---|---|---|
in_plane | placed on edge B-C: FY = 1 | total load | uniform |
out_plane | placed on edge B-C: FZ = 1 | total load | uniform |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Tip Displacement in Direction of Load (l=in_plane, m=tip_disp_y) | 0.08734 | 0.08833 | 1.13% |
Tip Displacement in Direction of Load (l=out_plane, m=tip_disp_z) | 0.5022 | 0.50057 | 0.32% |
Convergence %: 0.3% on Local Disp and SE | Max P: 6 | No. Equations: 234 | |
mvss011: 3D Simply Supported Rectangular Plate
Analysis Type: | Static |
Model Type: | 3D |
Comparison: | The MacNealHarder Accuracy Tests |
Reference: | MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Description: | A flat plate is simply supported on all four edges. One quarter of the plate is modeled using symmetry. The plate is loaded with two different loads, including uniform pressure and a point load at the center. Find the displacement at the center of the plate. |

Specifications
Element Type: | shell (2) | |
Units: | IPS | |
Dimensions: | length: 5 width: 1 thickness: 0.0001 | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 1.7472e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints | Location | Degrees of Freedom |
|---|---|---|
placed on edges A-D, C-D: placed on edge A-B: placed on edge B-C: | fixed in TransX, TransY, and TransZ fixed in TransY, RotX, and RotZ fixed in TransX, RotY, and RotZ |
Loads: | Location/Magnitude: | Distribution: | Spatial Variation: |
|---|---|---|---|
pressure | placed on all shells: pressure = 1e4 | total load per unit area | uniform |
point | placed on B: FZ = 1e4 | N/A | N/A |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Displacement @ Center (l=pressure, m=disp_z_cen) | 12.97 | 12.97 | 0.0% |
Displacement @ Center (l=point, m=disp_z_cen) | 16.96 | 16.81 | 0.88% |
Convergence %: 0.8% on Local Disp and SE | Max P: 9 | No. Equations: 438 | |
mvss012: 3D Clamped Rectangular Plate
Analysis Type: | Static |
Model Type: | 3D |
Comparison: | The MacNealHarder Accuracy Tests |
Reference: | MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Description: | One quarter of a rectangular plate, clamped on four edges, is modeled using symmetry. The plate is loaded with two different loads, including uniform pressure and a point load at center. Find the displacement at the center of the plate. |
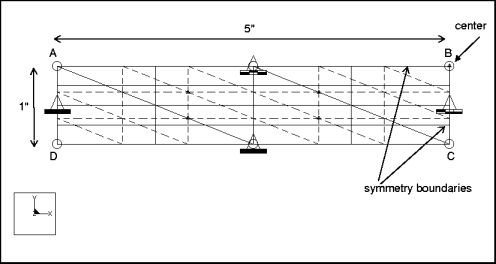
Specifications
Element Type: | shell (2) | |
Units: | IPS | |
Dimensions: | length: 5 width: 1 thickness: 0.0001 | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 1.7472e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints | Location | Degrees of Freedom |
|---|---|---|
placed on edges A-D, D-C: placed on edge A-B: placed on edge B-C: | fixed in all DOF fixed in TransY, RotX, and RotZ fixed in TransX, RotY, and RotZ |
Loads: | Location/Magnitude: | Distribution: | Spatial Variation: |
|---|---|---|---|
pressure | placed on all shells: pressure = 1e4 | per unit area | uniform |
point | placed on B: FZ = 1e4 | N/A | N/A |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Displacement @ Center (l=pressure, m=measure1) | 2.56 | 2.604 | 1.71% |
Displacement @ Center (l=point, m=measure1) | 7.23 | 7.168 | 0.85% |
Convergence %: 1.3% on Local Disp and SE | Max P: 9 | No. Equations: 625 | |
mvss013: 3D Hemispherical Shell
Analysis Type: | Static |
Model Type: | 3D |
Comparison: | The MacNealHarder Accuracy Tests |
Reference: | MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Description: | One quarter of an open hemisphere is modeled with symmetry and loaded with alternating point loads at 90  intervals on the equator. Find the radial displacement at any load point. intervals on the equator. Find the radial displacement at any load point. |

Specifications
Element Type: | shell (4) | |
Units: | IPS | |
Dimensions: (using a one-quarter model) | radius: 10 arc span: 90o thickness: 0.04 | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 6.825e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints | Location | Degrees of Freedom |
|---|---|---|
placed on curve A-C: placed on curve G-E: placed on point D | fixed in TransP, RotR, and RotT fixed in TransP, RotR, and RotT fixed in TransT |
Loads: | Location/Magnitude: | Distribution: | Spatial Variation |
|---|---|---|---|
placed on point C: FR = 1 placed on E: FR = 1 | N/A N/A | N/A N/A |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Radial Displacement @ Load (m=disp_rad) | 0.0924 | 0.0933 | 0.97% |
Convergence %: 0.6% on Local Disp and SE | Max P: 9 | No. Equations: 1965 | |
mvss014: 3D Cantilever Beam Twisted by 90

Analysis Type: | Static |
Model Type: | 3D |
Comparison: | The MacNealHarder Accuracy Tests |
Reference: | MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Description: | A cantilever beam, twisted by 90  , is subjected to in-plane and out-of-plane loads at the free end. Find the tip displacement in the direction of the load for each case. , is subjected to in-plane and out-of-plane loads at the free end. Find the tip displacement in the direction of the load for each case. |

Specifications
Element Type: | solid (2) | |
Units: | IPS | |
Dimensions: | length: 12 width: 1.1 thickness: 0.32 angle of twist 90o (from fixed to free end) | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 29e6 | Poisson's Ratio: 0.22 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on root surface: fixed in all DOF | |
Loads: | Location/Magnitude: | Distribution: | Spatial Variation: |
|---|---|---|---|
in_plane | placed on free end surface: FY = 1 | total load | uniform |
out_plane | placed on free end surface: FZ = 1 | total load | uniform |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Tip Displacement in Direction of Load (l=in_plane, m=disp_tip_y1) | 0.005424 | 0.005428 | 0.73% |
Tip Displacement in Direction of Load (l=out_of_plane, m=disp_tip_z1) | 0.001754 | 0.001760 | 0.342% |
Convergence %: 0.8% on Local Disp and SE | Max P: 5 | No. Equations: 590 | |
mvss015: 3D Scordelis-Lo Roof
Analysis Type: | Static |
Model Type: | 3D |
Comparison: | The MacNealHarder Accuracy Tests |
Reference: | MacNeal, R.H., and Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Description: | A Scordelis-Lo roof is one-quarter of an arched roof modeled using symmetry and loaded uniformly. Find the vertical displacement at the midpoint of the straight side (of the whole roof). |

Specifications
Element Type: | shell (1) | |
Units: | IPS | |
Dimensions: (using a one-quarter model) | length: 25 radius: 25 arc span: 40o thickness: 0.25 | |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 4.32e8 | Poisson's Ratio: 0 Thermal Expansion: 0 Conductivity: 0 |
Constraints | Location | Degrees of Freedom |
|---|---|---|
(UCS) (UCS) (UCS) | placed on curve A-B: placed on curve A-D: placed on curve C-D | fixed in TransZ, RotR, and RotT fixed in TransT, RotZ, and RotR fixed in TransR and TransT |
Loads: | Location/Magnitude: | Distribution: | Spatial Variation: |
|---|---|---|---|
placed on face A-B-C-D: FZ = 90 | per unit area | uniform |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Vertical Displacement @ Point B (m=disp_z_mid) | 0.3024 | 0.3008 | 0.53% |
Convergence %: 0.2% on Local Disp and SE | Max P: 7 | No. Equations: 148 | |
mvss016: 2D Axisymmetric Cylinder/Sphere
Analysis Type: | Static |
Model Type: | 2D Axisymmetric |
Reference: | NAFEMS, LSB1, No. IC 39 |
Description: | An axisymmetric cylinder and half-sphere vessel is loaded with uniform internal pressure. Find the hoop stress on the outer surface at point D. |

Specifications
Element Type: | 2D shell (4) | |
Units: | MKS | |
Dimensions: | radius: 1 thickness: 0.025 | |
Material Properties: | Mass Density: 0.007 Cost Per Unit Mass: 0 Young's Modulus: 210000 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints | Location | Degrees of Freedom |
|---|---|---|
constraint1 | placed on point A: placed on point E: | fixed in TransX and RotZ fixed in TransY |
Loads: | Location/Magnitude: | ||
|---|---|---|---|
load1 | placed on all 2D shell elements: internal pressure = 1 | ||
Comparison of Results Data
Theory | Structure1 | % Difference | |
|---|---|---|---|
Szz on outer surface | 38.5 | 38.62 | 0.3% |
Convergence %: 0.8% on Local Disp and SE | Max P: 7 | No. Equations: 72 | |
1 You cannot view the results information in the summary file. To view the results, you must define a result window for the Stress ZZ (Bottom), and query the value at point D.
mvss017: 2D Tapered Membrane with Gravity Load
Analysis Type: | Static |
Model Type: | Plane Stress |
Reference: | NAFEMS, LSB1, No. IC 2 |
Description: | A tapered membrane has uniform acceleration in the global X direction. Find the direct stress Sxx at point B. |

Specifications
Element Type: | 2D plate (2) | |
Units: | MKS | |
Dimensions: | thickness: 0.1 | |
Material Properties: | Mass Density: 0.007 Cost Per Unit Mass: 0 Young's Modulus: 210000 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | Location | Degrees of Freedom |
|---|---|---|
constraint1 | placed on curves A-B, B-C: placed on point B: | fixed in TransX fixed in TransX, TransY |
Loads: | Location/Magnitude: |
|---|---|
load1 | Global acceleration: GX=9.81 |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Stress XX at point B (m=measure1) | 0.247 | 0.247 | 0% |
Convergence %: 0.7% on Local Disp and SE | Max P: 7 | No. Equations: 248 | |
mvss018: 3D Z-Section Cantilevered Plate
Analysis Type: | Static |
Model Type: | 3D |
Reference: | NAFEMS, LSB1, No. IC 29 |
Description: | A Z-section cantilevered plate is subjected to a torque at the free end by two uniformly distributed edge shears. Find the direct stress Sxx at the mid-plane of the plate. |

Specifications
Element Type: | shell (6) | |
Units: | MKS | |
Dimensions: | length: 10 thickness: 0.1 | |
Material Properties: | Mass Density: 0.007 Cost Per Unit Mass: 0 Young's Modulus: 210000 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints | Location | Degrees of Freedom |
|---|---|---|
constraint1 | placed on curves A-B, B-C, and C-D: | fixed in TransX, TransY, and TransZ |
Loads: | Location/Magnitude: | Distribution | Spatial Variation |
|---|---|---|---|
load1 | placed on curve E-F: FZ=0.6 placed on curve G-H: FZ=0.6 | total load total load | uniform uniform |
Comparison of Results Data
Theory | Structure1 | % Difference | |
|---|---|---|---|
Sxx at mid-surface at point M | 108.8 | 110.02 | 1.1% |
Convergence %: 0.4% on Local Disp and SE | Max P: 7 | No. Equations: 870 | |
1 You cannot view the results information in the summary file. To view the results, you must define a result window for the measure Stress XX (Top and Bottom), and query the value at point M. Then average the top (118) and bottom (105.56) values.
mvss019: 3D Cylindrical Shell with Edge Moment
Analysis Type: | Static |
Model Type: | 3D |
Reference: | NAFEMS, LSB1, No. IC 19 |
Description: | A cylindrical shell in 3D space is loaded with a uniform normal edge moment on one edge. Find the outer surface tangential stress at point E. |

Specifications
Element Type: | shell (1) | |
Units: | MKS | |
Dimensions: | radius: 1 thickness: 0.01 | |
Material Properties: | Mass Density: 0.007 Cost Per Unit Mass: 0 Young's Modulus: 210000 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints | Location | Degrees of Freedom |
|---|---|---|
constraint1 | placed on curve A-B: placed on curves A-D and B-C: | fixed in all DOF fixed in TransZ, RotX, and RotY |
Loads: | Location/Magnitude: | Distribution | Spatial Variation |
|---|---|---|---|
load1 | placed on curve C-D: MZ=0.001 | force per unit length | uniform |
Comparison of Results Data
Theory | Structure1 | % Difference | |
|---|---|---|---|
Sxx on outer surface at point E | 60.0 | 59.6 | .67% |
Convergence %: 0.9% on Local Disp and SE | Max P: 5 | No. Equations: 66 | |
1 You cannot view the results information in the summary file. To view the results, you must define a result window for measure Stress XX (Top) with Face Grid on, and query the value at point E.
mvss020: Beam Sections
Analysis Type: | Static |
Model Type: | 3D |
Comparison: | Theory |
Reference: | Roark, R.J., and Young, W.C. Formulas for Stress and Strain. 5th Edition. NY: McGrawHill Book Co. 1982, p. 64. |
Description: | A cantilever beam is subjected to transverse loads in Y and Z and axial load in X . Find the deflection at the free end, the bending stress at the fixed end, and the axial stress along the beam. |

This Beam Sections model contains the following element types and corresponding results:
In all cases, the displacement results are dependent upon the direction of the load. Thus, in this problem, all the results listed as Deflection at Tip may be interpreted as positive or negative. |
Square Beam
Specifications
Element Type: | Square Beam | |
Units: | IPS | |
Dimensions: | a: 0.25 | |
Beam Properties: | Area: 0.0625 IYY: 0.000325521 Shear FY: 10001 CY: 0.125 | J: 0.000549316 IZZ: 0.000325521 Shear FZ: 10001 CZ: 0.125 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF | |
Load: | Location: | Magnitude: |
axial | placed on point B | FX=100 |
transverse y | placed on point B | FY=100 |
transverse z | placed on point B | FZ=100 |
1 Structure beams consider shear; however, the represented theoretical problem does not. The values for shear factor compensate for this.
Comparison of Results Data (Square Beam)
Load | Measure Name | Theory | Structure | % Difference |
|---|---|---|---|---|
Deflection at Tip: | ||||
axial | sq_d_x | 1.6e-3 | 1.6e-3 | 0% |
transverse y | sq_d_y | 9.216e1 | 9.216e1 | 0% |
transverse z | sq_d_z | 9.216e1 | 9.216e1 | 0% |
Stress: | ||||
axial | sq_s_ten | 1.6e3 | 1.6e3 | 0% |
transverse y | sq_s_bnd | 1.152003e6 | 1.15200e6 | 0% |
transverse z | sq_s_bnd | 1.152003e6 | 1.15200e6 | 0% |
Load | Lcl Disp & SE | Max P | No. Equations | |
|---|---|---|---|---|
Convergence: | ||||
axial | 0% | 2 | 264 | |
transverse y | 0% | 2 | 264 | |
transverse z | 0% | 2 | 264 | |
Rectangle Beam
Specifications
Element Type: | Rectangle Beam | |
Units: | IPS | |
Dimensions: | b: 1 d: 0.25 | |
Beam Properties: | Area: 0.25 IYY: 0.0208333 Shear FY: 10001 CY: 0.125 | J: 0.00438829 IZZ: 0.00130208 Shear FZ: 10001 CZ: 0.5 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF | |
Load: | Location: | Magnitude: |
axial | placed on point B | FX=100 |
transverse y | placed on point B | FY=100 |
transverse z | placed on point B | FZ=100 |
1Structure beams consider shear; however, the represented theoretical problem does not. The values for shear factor compensate for this.
Comparison of Results Data (Rectangle Beam)
Load | Measure Name | Theory | Structure | % Difference |
|---|---|---|---|---|
Deflection at Tip: | ||||
axial | rct_d_x | 4.0e-4 | 4.0e-4 | 0% |
transverse y | rct_d_y | 2.304e1 | 2.304e1 | 0% |
transverse z | rct_d_z | 1.44 | 1.44 | 0% |
Stress: | ||||
Load | Measure Name | Theory | Structure | % Difference |
axial | rct_s_ten | 4.0e2 | 4.0e2 | 0% |
transverse y | rct_s_bnd | 2.880e5 | 2.880e5 | 0% |
transverse z | rct_s_bnd | 7.200e4 | 7.200e4 | 0% |
Load | Lcl Disp & SE | Max P | No. Equations | |
|---|---|---|---|---|
Convergence: | ||||
axial | 0% | 2 | 264 | |
transverse y | 0% | 2 | 264 | |
transverse z | 0% | 2 | 264 | |
Hollow Rectangle Beam
Specifications
Element Type: | Hollow Rectangle Beam | |
Units: | IPS | |
Dimensions: | b: 1 bi: 0.875 d: 0.25 di: 0.125 | |
Beam Properties: | Area: 0.140625 IYY: 0.013855 Shear FY: 10001 CY: 0.125 | J: 0.00343323 IZZ: 0.00115967 Shear FZ: 10001 CZ: 0.5 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF | |
Load: | Location: | Magnitude: |
axial | placed on point B | FX=100 |
transverse y | placed on point B | FY=100 |
transverse z | placed on point B | FZ=100 |
1 Structure beams consider shear; however, the represented theoretical problem does not. The values for shear factor compensate for this.
Comparison of Results Data (Hollow Rectangle Beam)
Load | Measure Name | Theory | Structure | % Difference |
|---|---|---|---|---|
Deflection at Tip: | ||||
axial | hrct_d_x | 7.112e-4 | 7.111e-4 | 0.02% |
transverse y | hrct_d_y | 2.5869e1 | 2.5876e1 | 0.027% |
transverse z | hrct_d_z | 2.1653 | 2.1677 | 0.10% |
Stress: | ||||
Load | Measure Name | Theory | Structure | % Difference |
axial | hrct_s_ten | 7.112e2 | 7.111e2 | 0.01% |
transverse y | hrct_s_bnd | 3.2337e5 | 3.2336e5 | 0.003% |
transverse z | hrct_s_bnd | 1.0826e5 | 1.0826e5 | 0% |
Load | Lcl Disp & SE | Max P | No. Equations | |
|---|---|---|---|---|
Convergence: | ||||
axial | 0% | 2 | 264 | |
transverse y | 0% | 2 | 264 | |
transverse z | 0% | 2 | 264 | |
Channel Beam
Specifications
Element Type: | Channel Beam | |
Units: | IPS | |
Dimensions: | b: 1 di: 1 t: 0.125 tw: 0.125 | |
Beam Properties: | Area: 0.375 IYY: 0.0369466 Shear FY: 10001 CY: 0.625 | J: 0.00179932 IZZ: 0.0898438 Shear FZ: 10001 CZ: 0.645833 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF | |
Load: | Location: | Magnitude: |
axial | placed on point B | FX=100 |
transverse y | placed on point B | FY=100 |
transverse z | placed on point B | FZ=100 |
1 Structure beams consider shear; however, the represented theoretical problem does not. The values for shear factor compensate for this.
Comparison of Results Data (Channel Beam)
Load | Measure Name | Theory | Structure | % Difference |
|---|---|---|---|---|
Deflection at Tip: | ||||
axial | chnl_d_x | 2.6667e-4 | 2.666667e-04 | 0% |
transverse y | chnl_d_y | 3.339e-1 | 4.004507e-01 | 19.93% |
transverse z | chnl_d_z | 8.1198e-1 | 8.1198e-1 | 0% |
Stress: | ||||
Load | Measure Name | Theory | Structure | % Difference |
axial | chnl_s_ten | 2.6667e2 | 2.6667e2 | 0% |
transverse y | chnl_s_bnd | 2.087e4 | 2.087e4 | 0% |
transverse z | chnl_s_bnd | 5.244e4 | 5.244e4 | 0% |
Convergence: | ||||
Load | Lcl Disp & SE | Max P | No. Equations | |
axial | 0% | 4 | 264 | |
transverse y | 0% | 4 | 264 | |
transverse z | 0% | 4 | 264 | |
I-Section Beam
Specifications
Element Type: | I-Section Beam | |
Units: | IPS | |
Dimensions: | b: 1 di: 1 t: 0.125 tw: 0.125 | |
Beam Properties: | Area: 0.375 IYY: 0.0209961 Shear FY: 10001 CY: 0.625 | J: 0.00179932 IZZ: 0.0898438 Shear FZ: 10001 CZ: 0.5 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF | |
Load: | Location: | Magnitude: |
axial | placed on point B | FX=100 |
transverse y | placed on point B | FY=100 |
transverse z | placed on point B | FZ=100 |
1 Structure beams consider shear; however, the represented theoretical problem does not. The values for shear factor compensate for this.
Comparison of Results Data (I-Section Beam)
Load | Measure Name | Theory | Structure | % Difference |
|---|---|---|---|---|
Deflection at Tip: | ||||
axial | I_d_x | 2.6667e-4 | 2.6667e-4 | 0% |
transverse y | I_d_y | 3.3391e-1 | 3.3573e-1 | 0.54% |
transverse z | I_d_z | 1.4288 | 1.4296 | 0.05% |
Stress: | ||||
Load | Measure Name | Theory | Structure | % Difference |
axial | I_s_ten | 2.6667e2 | 2.6667e2 | 0% |
transverse y | I_s_bnd | 2.0870e4 | 2.0869e4 | 0.004% |
transverse z | I_s_bnd | 7.1442e4 | 7.14418e4 | 0.001% |
Load | Lcl Disp & SE | Max P | No. Equations | |
|---|---|---|---|---|
Convergence: | ||||
axial | 0% | 2 | 264 | |
transverse y | 0% | 2 | 264 | |
transverse z | 0% | 2 | 264 | |
L-Section Beam
Specifications
Element Type: | L-Section Beam | |
Units: | IPS | |
Dimensions: | b: 1 d: 1 t: 0.125 tw: 0.125 | |
Beam Properties: | Area: 0.25 IYY: 0.0105794 Shear FY: 10001 CY: 0.789352 | J: 0.00119955 IZZ: 0.0423177 Shear FZ: 10001 CZ: 0.433047 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF | |
Load: | Location: | Magnitude: |
axial | placed on point B | FX=100 |
transverse y | placed on point B | FY=100 |
transverse z | placed on point B | FZ=100 |
1 Structure beams consider shear; however, the represented theoretical problem does not. The values for shear factor compensate for this.
Comparison of Results Data (L-Section Beam)
Load | Measure Name | Theory | Structure | % Difference |
|---|---|---|---|---|
Deflection at Tip: | ||||
axial | L_d_x | 4.0e-4 | 4.0e-4 | 0% |
transverse y | L_d_y | 7.0892e-1 | 7.089233e-01 | 0.0004% |
transverse z | L_d_z | 2.8357 | 2.835700 | 0% |
Stress: | ||||
Load | Measure Name | Theory | Structure | % Difference |
axial | L_s_ten | 4e2 | 4e2 | 0% |
transverse y | L_s_ben | 5.5611e4 | 5.595900e+04 | 0.62% |
transverse z | L_s_ben | 1.228e5 | 1.227991e+05 | 0.0007% |
Load | Lcl Disp & SE | Max P | No. Equations | |
|---|---|---|---|---|
Convergence: | ||||
axial | 0% | 2 | 264 | |
transverse y | 0% | 2 | 264 | |
transverse z | 0% | 2 | 264 | |
Diamond Beam
Specifications
Element Type: | Diamond Beam | |
Units: | IPS | |
Dimensions: | b: 0.25 d: 0.25 | |
Beam Properties: | Area: 0.03125 IYY: 8.13802e5 Shear FY: 10001 CY: 0.125 | J: 0.000146484 IZZ: 8.13802e5 Shear FZ: 10001 CZ: 0.125 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF | |
Load: | Location: | Magnitude: |
axial | placed on point B | FX=100 |
transverse y | placed on point B | FY=100 |
transverse z | placed on point B | FZ=100 |
1 Structure beams consider shear; however, the represented theoretical problem does not. The values for shear factor compensate for this.
Comparison of Results Data (Diamond Beam)
Load | Measure Name | Theory | Structure | % Difference |
|---|---|---|---|---|
Deflection at Tip: | ||||
axial | dmnd_d_x | 3.2e-3 | 3.2e-3 | 0% |
transverse y | dmnd_d_y | 3.6864e2 | 3.6864e2 | 0% |
transverse z | dmnd_d_z | 3.6864e2 | 3.6864e2 | 0% |
Stress: | ||||
Load | Measure Name | Theory | Structure | % Difference |
axial | dmnd_s_ten | 3.2e3 | 3.2e3 | 0% |
transverse y | dmnd_s_bnd | 4.608e6 | 4.608e6 | 0% |
transverse z | dmnd_s_bnd | 4.608e6 | 4.608e6 | 0% |
Load | Lcl Disp & SE | Max P | No. Equations | |
|---|---|---|---|---|
Convergence: | ||||
axial | 0% | 2 | 264 | |
transverse y | 0% | 2 | 264 | |
transverse z | 0% | 2 | 264 | |
Solid Circle Beam
Specifications
Element Type: | Solid Circle Beam | |
Units: | IPS | |
Dimensions: | r: 0.25 | |
Beam Properties: | Area: 0.19635 IYY: 0.00306796 Shear FY: 10001 CY: 0.25 | J: 0.00613592 IZZ: 0.00306796 Shear FZ: 10001 CZ: 0.25 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF | |
Load: | Location: | Magnitude: |
axial | placed on point B | FX=100 |
transverse y | placed on point B | FY=100 |
transverse z | placed on point B | FZ=100 |
1 Structure beams consider shear; however, the represented theoretical problem does not. The values for shear factor compensate for this.
Comparison of Results Data (Solid Circle Beam)
Load | Measure Name | Theory | Structure | % Difference |
|---|---|---|---|---|
Deflection at Tip: | ||||
axial | crcl_d_x | 5.093e-4 | 5.092e-4 | 0.019% |
transverse y | crcl_d_y | 9.77848 | 9.77995 | 0.015% |
transverse z | crcl_d_z | 9.77848 | 9.77995 | 0.015% |
Stress: | ||||
axial | crcl_s_ten | 5.093e2 | 5.092e2 | 0.019% |
transverse y | crcl_s_bnd | 2.44462e5 | 2.44462e5 | 0% |
transverse z | crcl_s_bnd | 2.44462e5 | 2.44462e5 | 0% |
Load | Lcl Disp & SE | Max P | No. Equations | |
|---|---|---|---|---|
Convergence: | ||||
axial | 0% | 2 | 264 | |
transverse y | 0% | 2 | 264 | |
transverse z | 0% | 2 | 264 | |
Hollow Circle Beam
Specifications
Element Type: | Hollow Circle Beam | |
Units: | IPS | |
Dimensions: | ri: 0.25 | |
Beam Properties: | Area: 0.147262 IYY: 0.00287621 Shear FY: 100001 CY: 0.25 | J: 0.00575243 IZZ: 0.00287621 Shear FZ: 10001 CZ: 0.25 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF | |
Load: | Location: | Magnitude: |
axial | placed on point B | FX=100 |
transverse y | placed on point B | FY=100 |
transverse z | placed on point B | FZ=100 |
1 Structure beams consider shear; however, the represented theoretical problem does not. The values for shear factor compensate for this.
Comparison of Results Data (Hollow Circle Beam)
Load | Measure Name | Theory | Structure | % Difference |
|---|---|---|---|---|
Deflection at Tip: | ||||
axial | hcr_d_x | 6.7906e-4 | 6.7906e-4 | 0% |
transverse y | hcr_d_y | 1.04304e1 | 1.04331e1 | 0.025% |
transverse z | hcr_d_z | 1.04304e1 | 1.04332e1 | 0.026% |
Stress: | ||||
axial | hcr_s_ten | 6.7906e2 | 6.7906e2 | 0% |
transverse y | hcr_s_bnd | 2.6076e5 | 2.6075e5 | 0.003% |
transverse z | hcr_s_bnd | 2.6076e5 | 2.6076e5 | — |
Load | Lcl Disp & SE | Max P | No. Equations | |
|---|---|---|---|---|
Convergence: | ||||
axial | 0% | 2 | 264 | |
transverse y | 0% | 2 | 264 | |
transverse z | 0% | 2 | 264 | |
Ellipse Beam
Specifications
Element Type: | Ellipse Beam | |
Units: | IPS | |
Dimensions: | a: 1 b: 0.25 | |
Beam Properties: | Area: 0.785398 IYY: 0.19635 Shear FY: 10001 CY: 0.25 | J: 0.0461999 IZZ: 0.0122718 Shear FZ: 10001 CZ: 1 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF | |
Load: | Location: | Magnitude: |
axial | placed on point B | FX=100 |
transverse y | placed on point B | FY=100 |
transverse z | placed on point B | FZ=100 |
1 Structure beams consider shear; however, the represented theoretical problem does not. The values for shear factor compensate for this.
Comparison of Results Data (Ellipse Beam)
Load | Measure Name | Theory | Structure | % Difference |
|---|---|---|---|---|
Deflection at Tip: | ||||
axial | elps_d_x | 1.2732e-4 | 1.2732e-4 | 0% |
transverse y | elps_d_y | 1.527887e-1 | 1.531516e-01 | 0.24 % |
transverse z | elps_d_z | 2.4446 | 2.445098 | 0.02% |
Stress: | ||||
axial | elps_s_ten | 1.273239e2 | 1.27324e2 | 0% |
transverse y | elps_s_bnd | 1.527887e4 | 1.527887e4 | 0% |
transverse z | elps_s_bnd | 6.11155e4 | 6.111550e4 | 0% |
Load | Lcl Disp & SE | Max P | No. Equations | |
|---|---|---|---|---|
Convergence: | ||||
axial | 0% | 2 | 264 | |
transverse y | 0% | 2 | 264 | |
transverse z | 0% | 2 | 264 | |
Hollow Ellipse Beam
Specifications
Element Type: | Hollow Ellipse Beam | |
Units: | IPS | |
Dimensions: | a: 1 b: 0.25 ai: 0.875 | |
Beam Properties: | Area: 0.184078 IYY: 0.081253 Shear FY: 10001 CY: 0.25 | J: 0.0191184 IZZ: 0.00507832 Shear FZ: 10001 CZ: 1 |
Material Properties: | Mass Density: 0 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF | |
Load: | Location: | Magnitude: |
axial | placed on point B | FX=100 |
transverse y | placed on point B | FY=100 |
transverse z | placed on point B | FZ=100 |
1 Structure beams consider shear; however, the represented theoretical problem does not. The values for shear factor compensate for this.
Comparison of Results Data (Hollow Ellipse Beam)
Load | Measure Name | Theory | Structure | % Difference |
|---|---|---|---|---|
Deflection at Tip: | ||||
axial | hel_d_x | 5.4325e-4 | 5.4324e-4 | 0.0018% |
transverse y | hel_d_y | 3.6922e-1 | 3.7091e-1 | 0.45% |
transverse z | hel_d_z | 5.9075 | 5.9091 | 0.027% |
Stress: | ||||
axial | hel_s_ten | 5.4325e2 | 5.4324e2 | 0.0018% |
transverse y | hel_s_bnd | 3.6922e4 | 3.6921e4 | 0.0027% |
transverse z | hel_s_bnd | 1.4769e5 | 1.4768e5 | 0.0067% |
Load | Lcl Disp & SE | Max P | No. Equations | |
|---|---|---|---|---|
Convergence: | ||||
axial | 0% | 2 | 264 | |
transverse y | 0% | 2 | 264 | |
transverse z | 0% | 2 | 264 | |
mvss021:Thick-Walled Cylinder Under Internal Pressure
Analysis Type: | Static |
Model Type: | 3D |
Reference: | Roark, R.J., and Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Book Co., 5th edition, Table 32, Case 1. |
Description: | A thick-walled cylinder subjected to an internal pressure is free to expand in all directions. Obtain maximum radial and circumferential stresses. |

Specifications
Element Type: | tets (133) | |
Units: | IPS | |
Dimensions: | length: 20 Ro: 6 Ri: 4 | |
Material Properties: | Mass Density: 0.0002614 Cost Per Unit Mass: 0 Young's Modulus: 1.06e7 | Poisson's Ratio: 0.33 Thermal Expansion: 1.25e05 Conductivity: 9.254 |
Constraints | Location | Degrees of Freedom |
|---|---|---|
constraint1 | placed on point A: placed on point B: placed on point D: | fixed in TransX, TransY, and TransZ fixed in TransY fixed in TransY and TransZ |
Loads: | Location/Magnitude: | Distribution | Spatial Variation |
|---|---|---|---|
pressure | placed on all internal surfaces: pressure = 1000 | total load/unit area | uniform |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
 yy along edges C-E & F-G yy along edges C-E & F-G | 2600 | 2603.7325 | 0.14% |
 xx along edges C-E & F-G xx along edges C-E & F-G | 1000 | 999.1724 | 0.08% |
Multi-Pass Convergence %: The analysis converged to within 1% on measures. | Max P: 6 | No. Equations: 1875 | |
mvss022: Thin-Walled Spherical Vessel Under Its Own Weight
Analysis Type: | Static |
Model Type: | 3D Cyclic Symmetric |
Reference: | Roark, R.J., and Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Book Co., 5th edition, Table 29, Case 3c. |
Description: | A thin-walled half-spherical vessel is subjected to its own weight (gravity load). Obtain the hoop stress at points A and B. |

Specifications
Element Type: | shells (3) | |
Units: | IPS | |
Dimensions: | R: 10 | |
Material Properties: | Mass Density: 0.0002588 Cost Per Unit Mass: 0 Young's Modulus: 1.0e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints | Location | Degrees of Freedom |
|---|---|---|
constraint1 | Edges @  = 0 & = 0 &  = 90: = 90:Edge @ z = 0: Placed on point C @ r = 10,  = 0, z = 0: = 0, z = 0: | cyclical symmetry fixed in TransZ fixed in TransR, TransT, and TransZ |
Load: | Direction: | Magnitude: |
|---|---|---|
gravity | x y z | 0.0 386.4 0.0 |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
 zz at point A: zz at point A: | 1 | 0.987 | 1.3% |
 tt at point B: tt at point B: | -1 | -0.982 | 1.8% |
Multi-Pass Adaptive Convergence %: The analysis converged to within 4.9% on Local Displacement and Element Strain Energy. It converged to 1.7% on Global RMS Stress. | Max P: 9 | No. Equations: 773 | |
mvsl001: Static Analysis of Composite Lay-up
Analysis Type: | Static with Orthotropic Material Properties |
Model Type: | 3D |
Comparison: | Theory |
Reference: | Noor, A.K. and Mathers, M.D., "Shear-Flexible Finite-Element Models of Laminated Composite Plates and Shells." NASA TN D-8044; Langley Research Center, Hampton, Va. Dec. 1975. |
Description: | Determine maximum resultant bending moment and transverse deformation in a clamped, nine-layered, orthotropic square plate. |

Specifications
Element Type: | shell (4) | ||
Units: | IPS | ||
Dimensions: | length: 2.5 width: 2.5 thickness: 0.5 | ||
Shell Properties: | |||
Extensional Stiffness | A11=10.266 | A12=0.1252 | A16=0 |
A22=10.266 | A26=0 | ||
A66=0.3 | |||
ExtensionalBending Coupling Stiffness | B11=0 | B12=0 | B16=0 |
B22=0 | B26=0 | ||
B66=0 | |||
Bending Stiffness | D11=0.25965 | D12=0.0026082 | D16=0 |
D22=0.1681 | D26=0 | ||
D66=0.00625 | |||
Transverse Shear Stiffnesses | A55=0.275004 | A45=0 | A44=0.275004 |
Mass per Unit Area | 7.2915e5 | ||
Rotary Inertia per Unit Area | 1.5191e5 | ||
Thermal Resultant Coefficients: | |||
Force | N11=0 | N22=0 | N12=0 |
Moment | M11=0 | M22=0 | M12=0 |
Stress Recovery Locations | CZ | Ply Orientation (Degrees) | Material |
Location Reported for "Top" in Results | 0.25 | 0 | trniso1 |
Location Reported for "Bottom" in Results | 0.25 | 0 | trniso1 |
Material Properties: | |||
Mass Density: 0.00014583 | Cost Per Unit Mass: 0 | ||
Young's Moduli | E1=4e1 | E2=1 | E3=1 |
Poisson's Ratio | Nu21=0.25 | Nu31=0.25 | Nu32=0 |
Shear Moduli | G21=0.6 | G31=0.6 | G32= E2/[2*(1+Nu32)] |
Coefficients of Thermal Expansion | a1=0 | a2=0 | a3=0 |
Constraints: | symmetry constraints on edges B-C and C-D clamped on edges A-B and A-D | ||
Loads: | uniform pressure load over the entire surface = 1 | ||
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Displacement | 11.596 | 11.84151 | 2.11% |
Bending Moment 1 | 1.4094 | 1.41307 | 0.26% |
Convergence %: 1.1% on local displacement and element strain energy and 2.2 % on global RMS stress. | Max P: 3 | No. Equations: 76 | |
1 To verify this Creo Simulate result, create a query result window for the quantity Moment:Shell Resultant:XX. Show the result window and query for the value in the upper left corner of the model. This is obtained using View:Model Min. The absolute value of this negative number is greater than the value reported using View:Model Max and is reported here.