Présentation de l'analyse en fatigue
Ce document fournit des informations sur la fatigue et décrit la méthodologie appliquée par Creo Simulate dans l'analyse en fatigue. Il contient les rubriques suivantes :
• Cycles de déformation
Inclut les effets des contraintes résiduelles moyennes, la capture de cycle d'hystérésis et le comptage du cycle "rainflow".
• Facteurs affectant la durée de vie en fatigue
Inclut la taille des composantes, le type de charge, l'état de surface, le traitement de la surface (c.-à-d. traitements mécaniques, métallisation et traitements thermiques) et les effets des traitements de surface sur la limite de l'endurance.
La technologie de solveur intégrée avec l'analyse en fatigue Creo Simulate est fournie par nCode International. L'analyse en fatigue requiert une licence Fatigue Advisor disponible auprès de PTC.
Historique de la fatigue
La plupart des conceptions de composantes impliquent des pièces soumises à des charges fluctuantes ou cycliques. Ces charges incluent des contraintes fluctuantes ou cycliques qui entraînent souvent une rupture due à la fatigue. Environ 95 % de toutes les ruptures structurelles ont lieu au moyen d'un mécanisme de fatigue.
Les dommages causés au cours du processus de fatigue se cumulent et sont généralement irrécupérables en raison des points suivants :
• Il est pratiquement impossible de détecter des modifications progressives de comportement des matériaux dans le cadre d'un processus en fatigue ; les ruptures ont donc souvent lieu sans signe prémonitoire.
• Les périodes de repos, avec suppression de la contrainte de fatigue, ne permettent pas ou peu de corriger ou de récupérer.
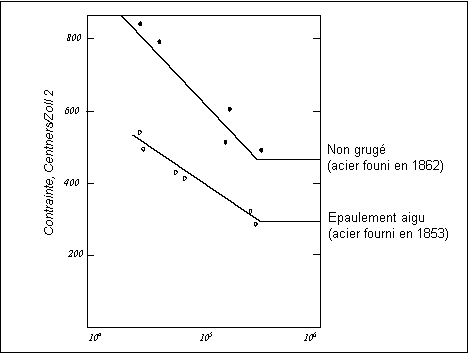
Il est bien connu que le bois et le métal peuvent être rompus à force de répéter des mouvements de pliage de grande amplitude en va-et-vient. Mais il a ensuite été découvert que des contraintes répétées peuvent engendrer une rupture même si l'amplitude de contrainte se situe apparemment bien dans la plage d'élasticité du matériau. Lorsque les problèmes de ruptures liées à la fatigue des essieux de chemin de fer se sont généralisés au milieu du XIXe siècle, l'attention a été portée sur les effets des charges cycliques. C'était la première fois qu'un grand nombre de composantes similaires étaient soumises à des millions de cycles à des niveaux de contrainte bien inférieurs à leur limite élastique de traction monotonique. Entre 1852 et 1870, August Wöhler, ingénieur allemand de chemins de fer, a mis en place et dirigé la première investigation sur la fatigue systématique.
Certaines des données d'August Wöhler portent sur l'acier d'essieu Krupp et ont été tracées en termes de contrainte nominale (S) contre le nombre de cycles jusqu'à rupture (N), ce qui constitue ce que l'on appelle désormais le diagramme S-N. Aujourd'hui encore, chaque courbe d'un diagramme de ce type est appelée une ligne Wöhler.
Remarque : 1centner = 50 kg, 1 zoll = 1 inch, 1 centner/zoll2 ~ 0.75 MPa
A peu près à la même époque, d'autres ingénieurs ont commencé à s'intéresser aux problèmes des ruptures associées aux charges fluctuantes pour les ponts, les équipements maritimes et les machines de production d'énergie. Au cours de la première partie du XXe siècle, un effort supplémentaire a été fait pour comprendre les mécanismes du processus de fatigue plutôt que de se contenter d'en observer les résultats. Ces activités ont finalement conduit, à la fin des années cinquante-début des années soixante, au développement de deux approches : l'une basée sur la mécanique élastique linéaire de la rupture (LEFM) expliquant la propagation des fissures et l'autre, appelée méthodologie de déformation locale Coffin-Manson, expliquant le commencement des fissures. Grâce à ces éclaircissements, les ingénieurs et concepteurs modernes ont pu créer des composantes proposant une meilleure résistance en fatigue sans se baser uniquement sur les expérimentations. D'un point de vue pratique, cette approche est beaucoup plus rentable.
Physique de la fatigue
Depuis 1830, il est accepté que le métal soumis à une charge répétitive ou fluctuante engendre une rupture à un niveau de contrainte inférieur à celui nécessaire pour causer une rupture dans le cadre d'une application unique de la même charge.
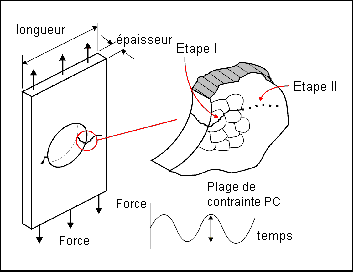
Le diagramme suivant présente une composante simple soumise à une force variable sinusoïdalement uniforme. Après une certaine période, une fissure commence à se former sur la circonférence du trou. Cette fissure se propage ensuite sur toute la composante jusqu'à ce que la section intacte restante ne puisse plus soutenir les contraintes imposées et que la composante génère un échec.
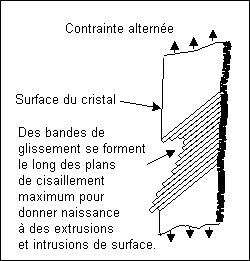
Le développement physique d'une fissure se divise généralement en deux étapes : la phase d'initiation de la fissure (Etape I) et la phase d'agrandissement de la fissure (Etape II). Les fissures liées à la fatigue sont générées par la libération d'une énergie de déformation en cisaillement. Le diagramme suivant indique comment les contraintes de cisaillement entraînent une déformation plastique locale le long des plans de glissement. La charge ayant un cycle sinusoïdal, les plans de glissement suivent un mouvement de va-et-vient comme un jeu de cartes, ce qui crée des petites extrusions et intrusions à la surface du cristal. Ces perturbations en surface ont une hauteur d'environ 1 à 10 microns et constituent des fissures embryonnaires.
Une fissure prend forme de cette manière jusqu'à atteindre la frontière du grain. A ce stade, le mécanisme est graduellement transféré vers le grain adjacent.
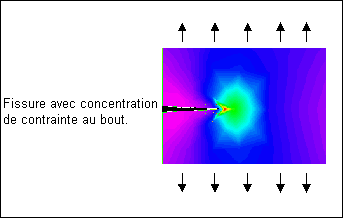
Lorsque la fissure prend la taille d'environ 3 grains, elle change de direction de propagation. L'agrandissement de l'Etape I suit la direction du plan de cisaillement maximal ou 45 ° dans la direction de la charge. Au cours de l'Etape II, le mécanisme physique de fatigue change. La fissure est désormais suffisamment grande pour constituer une concentration de contraintes géométriques. Une zone plastique de traction se crée à l'extrémité de la fissure, comme illustré dans le diagramme suivant. Après cette étape, la fissure se propage perpendiculairement à la direction de la charge appliquée.
De même que le mécanisme physique de fatigue est divisé en deux étapes, les méthodes d'analyse sont également, par convention, divisées en deux étapes. L'Etape I est généralement analysée à l'aide de l'approche de déformation locale (ou E-N), tandis que l'Etape II est analysée à l'aide d'une approche basée sur la mécanique de la rupture.
Pour une prédiction totale de la fatigue, une association des deux méthodes peut être possible :
Vie totale = Vie jusqu'à initiation + Vie nécessaire pour propager la fissure jusqu'à rupture
Cependant, la plupart des composantes d'ingénierie passent la plus grande partie de leur vie à une étape ou à l'autre. Dans ce cas, il est normal de ne prendre en compte qu'une seule étape, de manière conventionnelle. Par ex., pour les conceptions de véhicules au sol, la durée de vie est généralement régie par le temps jusqu'à initiation. Les composantes sont plutôt rigides et les matériaux assez fragiles. Lorsque l'initiation de la fissure a eu lieu, il faut un temps relativement court pour qu'elle se propage jusqu'à la rupture.
Par opposition, de nombreuses applications aérospatiales utilisent des composantes flexibles fabriquées à base de matériaux très ductiles. Dans ce cas, les fissures se propagent plutôt lentement et les approches de mécanique de la rupture sont généralement plus appropriées.
La nature physique de la fatigue n'était pas bien comprise au début des réflexions sur ce thème. August Wöhler avait donc opté pour une vision plus pragmatique de l'analyse en fatigue. La méthode qu'il a développée est par la suite devenue plus connue sous le nom d'analyse en fatigue de contrainte nominale (S-N). Cette méthode ne permettait pas de différencier les méthodes d'agrandissement des Etapes I et II et créait un lien entre la plage de contrainte nominale et le temps nécessaire jusqu'à la rupture.
Bien que l'analyse S-N soit toujours largement utilisée pour l'analyse en fatigue à base de tests, son principal inconvénient concerne les applications d'IAO. L'initiation de la fatigue est créée par des déformations plastiques locales, alors que l'analyse S-N utilise la contrainte élastique en entrée. Ainsi, l'analyse S-N n'est pas adaptée pour les analyses IAO sur les composantes contenant des zones locales de plasticité. C'est pour cette raison que les méthodes de déformation locale (ou E-N) sont universellement mieux adaptées. L'analyse en fatigue Creo Simulate utilise la méthode E-N.
Approche E-N
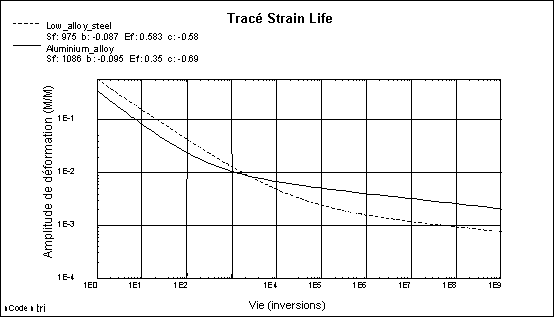
Lors d'un test de fatigue, des spécimens en forme de sablier de différents types de matériaux sont soumis à divers types de charges cycliques : flexion, torsion, traction et compression à petite échelle. L'approche E-N utilise ces tests pour mesurer la durée de vie en fatigue. Les résultats sont tracés en termes de déformation (E) contre cycles jusqu'à la rupture(N) sur un diagramme E-N. L'illustration ci-après représente un diagramme E-N classique pour un acier faiblement allié et un alliage d'aluminium.
Creo Simulate utilise un ensemble générique de propriétés de fatigue pour modéliser les aciers faiblement alliés, les aciers non alliés, les alliages d'aluminium et les alliages de titane. Ces propriétés génériques ont été compilées par Baumel Jr. et Seeger et sont connues sous le nom de Loi de matériaux uniforme (Uniform Material Law). Même si l'on ne peut pas s'attendre à en obtenir des durées de vie en fatigue précises pour une utilisation pratique, elles sont idéales pour déterminer si une composante est susceptible de rencontrer des problèmes liés à la fatigue et si une analyse plus détaillée est nécessaire avant la mise en service. Pour plus d'informations sur la Loi de matériaux uniforme (Uniform Material Law), consultez le manuel
Materials Science Monographs, 61, "Materials Data for Cyclic Loading, Supplement 1." La section suivante traite de deux aspects de la théorie de la fatigue qui sont essentiels pour bien comprendre comment Fatigue Advisor mesure la fatigue :
Cycles de déformation
Avant d'étudier plus en détail la procédure E-N, il peut être utile de comprendre les trois différents types de déformations cycliques qui contribuent au processus de fatigue. Les descriptions et diagrammes suivants expliquent chaque type séparé.
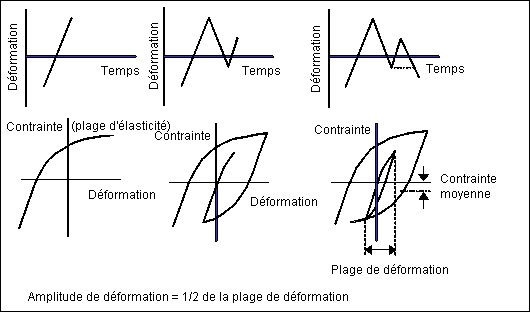
La première figure illustre un cycle de déformation intégralement inversé avec une forme sinusoïdale. Il s'agit d'une condition de charge idéalisée généralement présente dans les arbres rotatifs fonctionnant à vitesse constante sans surcharges. Il s'agit également du type de cycle de déformation utilisé pour la plupart des tests de fatigue. Pour ce type de cycle, les déformations maximale (
 max.
max.) et minimale (
 min.
min.) ont une intensité égale, mais un signe opposé. Généralement, la déformation de traction est considérée comme positive et la déformation de compression comme négative. La plage de déformation,
 r
r, correspond à la différence algébrique entre les déformations maximale et minimale d'un cycle.
L'amplitude de déformation,
 a
a, correspond à la moitié de la plage de déformation.
 a
a =
 r/2
r/2 = (
 max
max –
 max.
max.) / 2
La deuxième figure illustre la situation plus générale dans laquelle les déformations maximale et minimale ne sont pas égales. Dans ce cas, elles sont toutes deux de traction et définissent un décalage moyen,
 m
m = (
 max.
max. +
 min.
min.) / 2, pour la charge cyclique.
Comme indiqué ci-avant, la plupart des données de fatigue de base sont recueillies à l'aide de charges intégralement inversées. Ces données ne sont donc pas directement applicables pour les cycles de déformation ayant une moyenne différente de zéro (
 m
m
0). Afin d'établir des estimations de durée de vie plus réalistes pour les cycles de déformation avec contrainte moyenne de traction ou de compression, les résultats des tests menés à l'aide de charges intégralement inversées sont corrigés. Le choix de l'approche corrective à utiliser varie selon le fait que la contrainte moyenne est principalement de traction ou de compression.
La raison à cela est illustrée dans le tracé suivant qui présente schématiquement les effets de la contrainte moyenne sur la courbe déformation-vie (E-N). D'un point de vue conceptuel, la contrainte moyenne de traction agit en ouvrant une fissure tandis que la contrainte moyenne de compression tente de la garder fermée. Généralement, les effets sont concentrés à l'extrémité de longue vie du diagramme, avec la contrainte moyenne de traction réduisant la vie et la contrainte moyenne de compression qui la prolonge.
Etant donné que les tests requis pour calculer des courbes E-N pour une plage de contraintes moyennes sont assez chers, plusieurs relations empiriques ont été développées pour modéliser les effets de la contrainte moyenne. Parmi toutes les méthodes proposées, deux sont plus largement acceptées :
• Approche Smith, Watson, Topper
• Correction Morrow
Pour les séquences de charge principalement de traction par nature, l'approche Smith, Watson, Topper est plus conventionnelle et donc recommandée. Pour les cas où la charge est principalement de compression, particulièrement pour les cycles entièrement de compression, la correction Morrow peut être utilisée pour fournir des estimations de durée de vie plus réalistes.
Creo Simulate utilise les deux méthodes et la plus appropriée est automatiquement choisie. Pour plus d'informations sur l'approche Smith, Watson, Topper, consultez le manuel
"A Stress-Strain Function for the Fatigue of Metals", Journal of Materials, Vol. 5, No. 4, 1970. Pour plus d'informations sur la correction Morrow, consultez le manuel
"Fatigue Design Handbook", Advances in Engineering, Vol. 4, Society of Automotive Engineers, 1968.
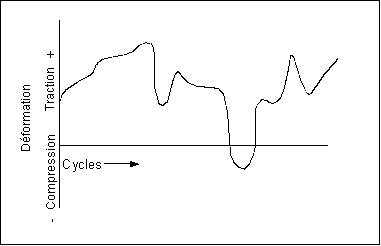
La figure suivante illustre un répétition de charge à amplitude variable plus complexe et plus proche des déformations cycliques présentes dans les structures réelles.
Pour les charges à amplitude variable, il est nécessaire d'extraire les cycles d'endommagement à la fatigue à partir du signal, puis d'évaluer les dommages causés par chaque cycle. Les dommages totaux correspondent à la somme des dommages causés par chaque cycle individuel. Chaque cycle de fatigue est extrait par un processus connu sous le nom de capture de cycle d'hystérésis. Les lieux géométriques de la contrainte et de la déformation sont tracés comme indiqué dans le diagramme suivant.
Lorsqu'un cycle d'hystérésis contrainte-déformation est fermé, la plage de déformation et la contrainte moyenne sont renvoyées et les dommages sont calculés à l'aide de la courbe E-N modifiée pour la correction de la contrainte moyenne. Cette analyse est menée sur l'intégralité du signal de durée de déformation jusqu'à ce que tous les cycles aient été extraits et que les dommages totaux aient été calculés. Un algorithme très efficace a été développé pour effectuer l'extraction des cycles. Il s'agit du comptage de cycle "rainflow". C'est cet algorithme que Creo Simulate utilise.
Creo Simulate utilise normalement une solution élastique linéaire pour déterminer les déformations pseudoélastiques d'un composant. En d'autres termes, la solution ignore la plasticité. Avant de continuer l'analyse en fatigue, ces déformations sont automatiquement converties en déformations élastique-plastique non linéaires à l'aide de la relation de Neuber.
Facteurs affectant la durée de vie en fatigue
Comme indiqué ci-avant, la courbe E-N est dérivée des tests de contrôle de déformation basés sur des spécimens en forme de sablier.
Un test standard de fatigue intégralement inversée est utilisé pour déterminer une relation E-N de ligne de base pour un spécimen poli d'un diamètre d'environ 6 mm. Tandis que la fatigue ou la limite d'endurance mesurée dans ce test est représentée par

'
e, une composante en service a une limite inférieure,
 e
e, qui reflète les modifications apportées à un spécimen en dehors du laboratoire. Plus particulièrement pour les aciers, plusieurs relations empiriques expliquent la variation de
 e
e comme résultant des points suivants :
• Taille de composante, Csize
• Type de charge, Cload
• Effets des grugeages, Cnotch
• Effets de l'état de surface, Csur < 1 (favorise l'agrandissement de la fissure)
• Effets du traitement de surface, Csur > 1 (empêche l'agrandissement de la fissure)
Pour expliquer ces effets, des facteurs de modification spécifiques sont généralement appliqués au résultat du test de sorte que :


e
= '
eC
notchC
sizeC
loadC
sur......
où l'inverse du produit, CnotchCsizeCloadCsur, est dans son ensemble connu comme le facteur Kf de réduction de la résistance en échec :
Kf = 1 / (CnotchCsizeCloadCsur......)
Il est très important de se rappeler que tous les facteurs de modification sont empiriques, conventionnels et généralement uniquement applicables à l'acier. Ils ne fournissent que très peu, voire pas du tout, d'informations fondamentales sur le processus de fatigue en lui-même autres que les tendances approximatives. Ils ne doivent tout particulièrement pas être utilisés dans les zones en dehors de leur applicabilité mesurée.
Consultez les rubriques suivantes pour en savoir plus sur les facteurs qui influencent la durée de vie en fatigue :
Influence de la taille de la composante
La fatigue des métaux est causée par la nucléation et l'agrandissement consécutif des défauts comme les fissures sous l'influence d'un champ de contrainte alterné. Selon la théorie, la rupture commence au lien le plus faible, le cristal métallique le plus favorablement orienté par ex., puis s'agrandit vers les grains moins favorablement orientés jusqu'à la rupture finale. Il paraît logique et raisonnable de supposer que plus le volume du matériau soumis à la contrainte alternée est grand, plus la probabilité de trouver le lien le plus faible rapidement est grande. Les données de test confirment la présence des effets relatifs à la taille, particulièrement dans le cas des pliages et torsions.
Le gradient de contraintes constitué dans la section, par pliage et, de manière moins importante, par torsion, concentre plus de 95 % de la contrainte de surface maximale dans une couche mince de matériau de surface. Dans les grandes sections, ce gradient de contraintes est moins accentué que dans les sections plus petites. Ainsi, le volume de matériau disponible et pouvant contenir un défaut critique est supérieur, d'où une résistance en fatigue réduite. Les effets sont plus restreints pour une traction axiale où le gradient de contraintes est nul. La valeur de Csize est estimée à partir de l'un des éléments suivants.
Si le diamètre de l'arbre spécimen de test est d < 6 mm :
Csize = 1
Si le diamètre de l'arbre spécimen de test est 6 mm < d < 250 mm :
Csize = 1.189d-0.097
Les effets de la taille sont particulièrement importants pour l'analyse des arbres rotatifs, comme il peut y en avoir dans les groupes motopropulseurs des véhicules.
Pour les cas où les composantes n'ont pas de section arrondie, l'équation suivante calcule un diamètre équivalent, deq, pour une section rectangulaire sous pliage avec largeur (w) et épaisseur (t) :
deq2 = 0.65wt
Influence du type de charge
Les données de fatigue mesurées à l'aide d'un type de charge cyclique, la traction axiale par exemple, peuvent être "corrigées" pour représenter les données qui auraient été obtenues si le test avait été effectué à l'aide d'une autre méthodologie de charge, comme la torsion ou le pliage. Le test standard de pliage en rotation exige que les tests soient effectués sous des conditions de pliage intégralement inversé.
En passant d'une condition de charge à une autre, les valeurs de Cload à utiliser avec la limite d'endurance
 e
e sont détaillées ci-après :
Charge mesurée | | Charge cible | Charge C |
Axial | vers | Pliage | 1,25 |
Axial | vers | Torsion | 0,725 |
Pliage | vers | Torsion | 0,58 |
Pliage | vers | Axial | 0,8 |
Torsion | vers | Axial | 1,38 |
Torsion | vers | Pliage | 1,72 |
Ainsi, en utilisant les valeurs de ce tableau, si une charge de traction axiale produit une déformation de
 e
e, la déformation produite sous une charge de pliage serait de 1.25
 e
e.
Outre l'influence sur la limite d'endurance, les conditions de charge peuvent également influencer la pente Basquin, b, utilisée pour le traçage de la courbe E-N sur une échelle log-log. Ces effets sont généralement pris en compte par la modification de la déformation à 10
3 cycles,
 3
3 et
 e
e. Les facteurs suivants sont utilisés pour définir C'load, le facteur de modification
 3
3 :
Charge mesurée | | Charge cible | Charge C |
Axial | vers | Torsion | 0,82 |
Pliage | vers | Torsion | 0,82 |
Torsion | vers | Axial | 1,22 |
Torsion | vers | Pliage | 1,22 |
Influence de l'état de surface
Une très grande partie des ruptures liées à la fatigue germe à la surface des composantes : les conditions de la surface constituent donc un facteur très important dans l'influence de la résistance en fatigue. Diverses conditions de surface sont généralement jugées par rapport au spécimen standard poli de laboratoire. Normalement, les rayures, piqûres, marques d'usinage, etc., influencent la résistance en fatigue en augmentant les contraintes supplémentaires qui favorisent le processus de nucléation des fissures.
Le diagramme ci-après démontre que les aciers à forte résistance sont plus négativement affectés par un état de surface rugueux que les aciers plus souples. Ainsi, le facteur de correction de l'état de surface, Csur < 1, est étroitement lié à la résistance à la traction. Dans cet exemple, le facteur de correction de l'état de surface permet de catégoriser la finition en termes qualitatifs, par ex. poli, usiné et forgé.
Sachez que certaines des courbes présentées dans cette figure comprennent des effets autres que l'état de surface. Par ex., les courbes de forgeage et de laminage à chaud incluent les effets de la décarburation.
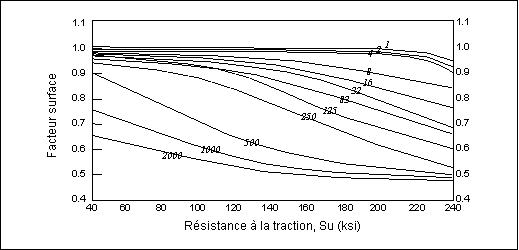
Les autres diagrammes présentent le facteur de correction de l'état de surface de manière plus quantitative à l'aide d'une mesure quantitative de la rugosité de la surface, comme RA (moyenne quadratique) ou AA (moyenne arithmétique). Le diagramme suivant présente les effets de la rugosité de la surface sur le facteur de correction de l'état de surface.
Les valeurs de rugosité de surface associées à chaque processus de fabrication sont disponibles dans divers manuels, comme dans l'exemple ci-après :
Type de finition (microns) | Rugosité de la surface |
Forme de tour | 2,67 |
Partiellement poli à la main | 0,15 |
Poli à la main | 0,13 |
Sol | 0,18 |
Superfinition | 0,18 |
Meulé et poli | 0,05 |
Influence qualitative du traitement de la surface
Tout comme pour l'état de surface, le traitement de la surface peut avoir une influence importante sur la résistance en fatigue, particulièrement sur la limite d'endurance. L'effet le plus net du traitement est de modifier l'état de la contrainte résiduelle à la surface libre.
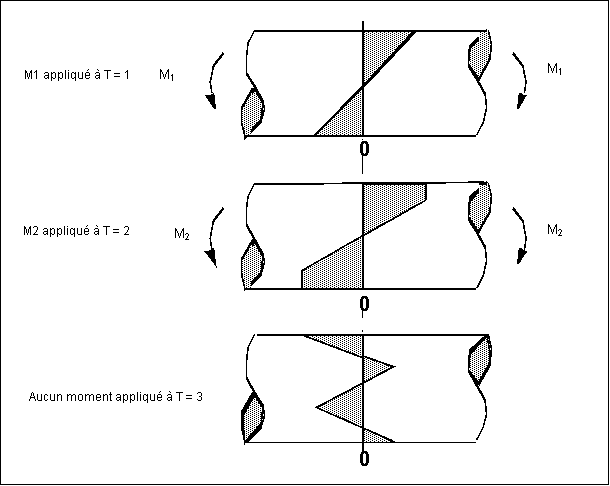
Les contraintes résiduelles ont lieu lorsque la déformation plastique n'est pas distribuée uniformément sur l'intégralité de la section de la composante en cours de déformation. Les figures précédentes présentaient le cas d'une barre de métal ayant une surface déformée en traction par pliage.
• Au temps T=1, le moment fléchissant M1 est appliqué et se trouve dans la plage d'élasticité.
• Au temps T=2, le moment fléchissant a augmenté jusqu'à M2, la limite élastique (Sy) a été atteinte et la surface subit une déformation plastique.
• Lorsque la force externe est supprimée, les régions déformées plastiquement empêchent les régions élastiques adjacentes de rétablir intégralement leur élasticité à la condition sans déformation. Ainsi, les régions déformées élastiquement conservent une traction résiduelle et les régions déformées plastiquement sont dans un état de compression résiduelle. Le résultat est la distribution des contraintes au temps T=3.
Dans de nombreux cas, la contrainte résiduelle peut être considérée comme identique aux contraintes produites par une force externe. Ainsi, la présence d'une contrainte résiduelle de compression à la surface d'une composante réduit efficacement la probabilité d'une rupture liée à la fatigue.
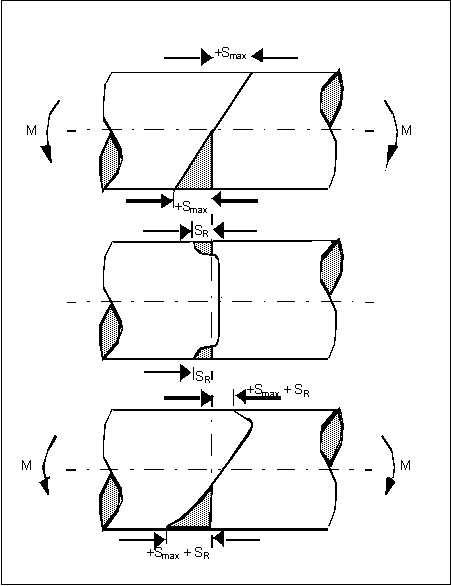
La figure précédente illustre la superposition de la contrainte appliquée et de la contrainte résiduelle.
• Le schéma supérieur présente une distribution de contrainte élastique dans une poutre sous un moment fléchissant M sans contrainte résiduelle.
• Dans le schéma central, vous pouvez voir les détails d'une distribution de contrainte résiduelle classique associée à un traitement de surface mécanique comme le grenaillage. Remarquez que la contrainte de compression à la surface est compensée par une contrainte de traction équivalente à l'intérieur de la section.
• Dans le schéma inférieur, vous pouvez voir la distribution résultant de la sommation algébrique de la contrainte appliquée (causée par le moment fléchissant M) et de la contrainte résiduelle. Remarquez que la contrainte de traction maximale à la surface a été réduite de la quantité de la contrainte résiduelle. De plus, le pic de contrainte de traction s'est déplacé à l'intérieur de la poutre. L'intensité de cette contrainte dépend du gradient de la contrainte appliquée et de la distribution de la contrainte résiduelle. Dans ces conditions, l'initiation de la fissure sous-surface est possible.
D'un point de vue global, les traitements de surface sont divisés en traitements mécaniques, thermiques et de métallisation. Les deux premiers processus fournissent une couche de compression, tandis que le processus de métallisation fournit une contrainte résiduelle de traction. Vous trouverez ci-après la description détaillée de chaque processus :
• Traitements mécaniques : les principales méthodes commerciales d'introduction de contraintes de compression résiduelles sont le laminage à froid et le grenaillage. Même si une certaine altération de la résistance du matériau a lieu en raison de l'écrouissage, l'amélioration de la résistance en fatigue est principalement due à la contrainte de surface de compression. L'enroulage de surface, particulièrement adapté aux grandes pièces, est fréquemment utilisé pour les composantes critiques telles que les vilebrequins et les surfaces de type palier des essieux de chemin de fer. Les boulons avec filetage enroulé possèdent généralement une résistance en fatigue deux fois supérieure à celle des filetages à usinage conventionnel.
Le grenaillage, qui consiste à projeter de l'acier fin ou de la fonte sur la surface d'une composante, est particulièrement bien adapté au traitement de pièces produites avec des petites masses.
Il est important de se rappeler que le laminage à froid et le grenaillage offrent leurs meilleurs effets à des durées de vie prolongées. A des durées de vie courtes, ils ont peu, voire pas d'effet du tout.
Comme pour les autres facteurs de modification, des facteurs de correction peuvent être utilisés pour expliquer les effets de ces contraintes de compression induites mécaniquement en ajustant la limite d'endurance
 e
e. Généralement, le facteur associé au grenaillage est d'environ 1.5 à 2.0.
• Traitements thermiques : les traitements thermiques sont des processus basés sur la diffusion de carbone (carburation) ou d'azote (nitruration) sur et dans la surface d'une composante en acier. Ces deux types d'atomes sont interstitiels, c.-à-d. qu'ils occupent les espaces entre les atomes de fer adjacents et augmentent donc la résistance de l'acier et sont la cause d'une contrainte résiduelle de compression laissée sur la surface par des changements volumétriques.
La carburation est généralement un processus en trois étapes :
◦ Groupement des composantes en acier dans des boîtes contenant des solides carbonés
◦ Fermeture pour exclure l'atmosphère
◦ Chauffage à environ 900 °C pendant une période dépendant de la profondeur requise
Les composantes peuvent également être chauffées dans un four en présence d'un gaz carburant chaud comme le gaz naturel. Ce processus présente l'avantage d'être plus rapide et plus précis. De plus, le cycle de carburation peut être suivi par un cycle de diffusion sans agent carburant présent. Ainsi, certains atomes de carbone sont diffusés davantage dans la composante afin de réduire les gradients.
Le processus de nitruration est très similaire à la carburation au gaz, à ceci près que le gaz ammoniac est utilisé et que les composantes sont plongées à des températures inférieures. Généralement, 48 heures à environ 550 degrés Celsius donnent une profondeur nitrurée d'environ 0,5 mm. La nitruration est tout particulièrement adaptée au traitement de composants entaillés finis comme des engrenages et des arbres rainurés. L'efficacité du processus est illustrée dans le tableau suivant :
| Limite d'endurance (MPa) |
Géométrie | Non nitruré | Nitruré |
Non grugé | 310 | 620 |
Grugeage semi-circulaire | 175 | 600 |
Grugeage en V | 175 | 550 |
• Métallisation : la métallisation au chrome et au nickel des composantes en acier peut réduire la limite d'endurance de plus de la moitié du fait de la création de contraintes résiduelles de traction à la surface. Ces contraintes de traction sont le résultat direct du processus de métallisation en lui-même. Comme dans le cas des contraintes de surface induites mécaniquement, les effets de la métallisation sont plus prononcés pour une durée de vie de spectre plus longue et avec des matériaux à plus forte résistance.
L'introduction d'une contrainte résiduelle de compression avant le processus de métallisation, comme le grenaillage ou la nitruration, peut réduire les effets indésirables de la métallisation. Le recuit des composantes après la métallisation, qui soulage les tractions, est une autre approche possible.
Effets quantitatifs des traitements de la surface sur la limite de l'endurance (aciers)
Les effets des traitements de la surface dépendent de l'état de surface. L'augmentation de la contrainte de limite d'endurance due au traitement de la surface est indiquée dans le tableau suivant :
| Augmentation de la limite d'endurance |
Finition | Grenaillé | Laminé à froid | Nitruré |
Poli | +15 % | +50 % | +100 % |
Sol | +20 % | +0 % | +100 % |
Usiné | +30 % | +70 % | +100 % |
Laminé à chaud | +40 % | +0 % | +100 % |
Moulé | +40 % | +0 % | +100 % |
Forgé | +100 % | +0 % | +100 % |
Quelle que soit la correction apportée par l'état de surface, l'application d'un traitement de surface a un effet consécutif, présenté dans le tableau précédent. Par exemple, si l'usinage réduit la limite d'endurance de 30 %, alors d'après ce tableau, vous pouvez voir que lle laminage à froid permet de récupérer cette perte en augmentant la limite de 70 %.

 max.) et minimale (
max.) et minimale ( min.) ont une intensité égale, mais un signe opposé. Généralement, la déformation de traction est considérée comme positive et la déformation de compression comme négative. La plage de déformation,
min.) ont une intensité égale, mais un signe opposé. Généralement, la déformation de traction est considérée comme positive et la déformation de compression comme négative. La plage de déformation,  r, correspond à la différence algébrique entre les déformations maximale et minimale d'un cycle.
r, correspond à la différence algébrique entre les déformations maximale et minimale d'un cycle. r =
r =  max. –
max. –  min.
min. a, correspond à la moitié de la plage de déformation.
a, correspond à la moitié de la plage de déformation. a =
a =  r/2 = (
r/2 = ( max –
max –  max.) / 2
max.) / 2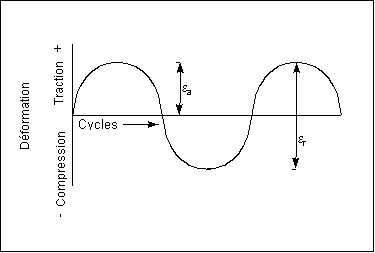
 m = (
m = ( max. +
max. +  min.) / 2, pour la charge cyclique.
min.) / 2, pour la charge cyclique.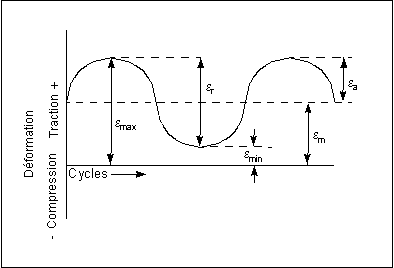
 m
m 0). Afin d'établir des estimations de durée de vie plus réalistes pour les cycles de déformation avec contrainte moyenne de traction ou de compression, les résultats des tests menés à l'aide de charges intégralement inversées sont corrigés. Le choix de l'approche corrective à utiliser varie selon le fait que la contrainte moyenne est principalement de traction ou de compression.
0). Afin d'établir des estimations de durée de vie plus réalistes pour les cycles de déformation avec contrainte moyenne de traction ou de compression, les résultats des tests menés à l'aide de charges intégralement inversées sont corrigés. Le choix de l'approche corrective à utiliser varie selon le fait que la contrainte moyenne est principalement de traction ou de compression.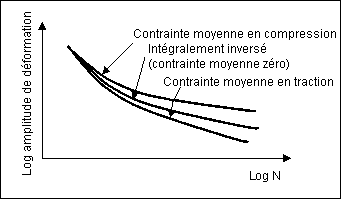
 'e, une composante en service a une limite inférieure,
'e, une composante en service a une limite inférieure,  e, qui reflète les modifications apportées à un spécimen en dehors du laboratoire. Plus particulièrement pour les aciers, plusieurs relations empiriques expliquent la variation de
e, qui reflète les modifications apportées à un spécimen en dehors du laboratoire. Plus particulièrement pour les aciers, plusieurs relations empiriques expliquent la variation de  e comme résultant des points suivants :
e comme résultant des points suivants :
 e = 'eCnotchCsizeCloadCsur......
e = 'eCnotchCsizeCloadCsur...... e sont détaillées ci-après :
e sont détaillées ci-après : e, la déformation produite sous une charge de pliage serait de 1.25
e, la déformation produite sous une charge de pliage serait de 1.25 e.
e. 3 et
3 et  e. Les facteurs suivants sont utilisés pour définir C'load, le facteur de modification
e. Les facteurs suivants sont utilisés pour définir C'load, le facteur de modification  3 :
3 :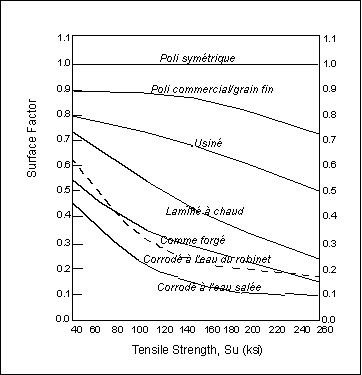
 e. Généralement, le facteur associé au grenaillage est d'environ 1.5 à 2.0.
e. Généralement, le facteur associé au grenaillage est d'environ 1.5 à 2.0.