Особые соображения относительно модели объема жидкости (VOF)
Сравнение модели VOF с моделью смеси
В концепции однородного многофазного моделирования Эйлера обе модели - модель объема жидкости (VOF) и модель смеси Эйлера - решают один тот же набор управляющих уравнений для смеси (осредненной). Однако в их основе лежат различные физические механизмы, и поэтому они применяются к различным многофазным режимам потока.
• Модель смеси - предназначена для двух или более фаз (жидкость или твердые частицы), которые обрабатываются как взаимно проникающие континуумы. В ней ищется решение для уравнения моментов смеси и уравнений энергии, а межфазовый интерфейс не отслеживается или не наблюдается ясных интерфейсов. Приложения модели смеси включают состоящие из частиц потоки с низким содержанием, потоки пузырьков и потоки капелек, оседание частиц и циклонные сепараторы. Можно также использовать модель смеси с предписанными относительными скоростями для дисперсных фаз, чтобы моделировать неоднородные многофазные потоки.
• Модель VOF - представляет собой метод, связанный с отслеживанием нестационарной поверхности, предназначенным для двух или более несмешивающихся жидкостей, где предметом исследования является положение межфазового интерфейса. В модели VOF для всех фаз используется один набор уравнений моментов смеси и уравнений энергии, и решение ищется неявно. Доли объема фаз получаются с помощью точных явных или неявных алгоритмов времени с адвективными схемами высшего порядка для нахождения резких границ раздела между парой фаз. Типовые приложения модели VOF включают слоистые потоки, потоки со свободной поверхностью, заполнение, расплескивание, движение больших пузырьков в жидкости, движение жидкости после прорыва перемычки, прогнозирование разрушения струи (поверхностное натяжение) и отслеживание любых интерфейсов жидкость-газ.
Формулировка VOF предполагает, что две жидкости (или фазы) или более не смешиваются и не проникают друг в друга. Поэтому в любой заданной ячейке контрольного объема по доле объемов локальных фаз можно определить, содержит ли ячейка только одну из фаз или смесь фаз. Например, для фазы qth, если доля объема в ячейке равна αq, то возможно выполнение только следующих трех условий:
◦ αq = 0: ячейка свободна от фазы qth
◦ αq = 1: ячейка заполнена фазой qth фазы
◦ 0 < αq < 1: ячейка содержит интерфейс между фазой q-й и одной или несколькими другими фазами.
Поэтому можно выполнить отслеживание интерфейсов между фазами путем решения транспортного уравнения для доли объема одной или нескольких фаз.
Эффект поверхностного натяжения
Поверхностное натяжение - это тенденция эластичной поверхности жидкости стремиться к наименьшей из возможных площади поверхности. Рассмотрим пузырек воздуха в жидкости. Внутри пузырьков равнодействующая сила всех сил, действующих на молекулу, равна нулю. В интерфейсах жидкость-воздух возникает поверхностное натяжение, поскольку притяжение молекул жидкости друг к другу больше по причине когезии (сцепления одинаковых молекул), чем к молекулам в воздухе по причине адгезии (сцепления разных молекул). Суммарное воздействие представляет собой силу, направленную внутрь по радиусу к поверхности жидкости, что приводит к стягиванию пузырьков. Давление внутри пузырьков увеличивается, чтобы уравновесить силу притяжения между молекулами.
• Модель непрерывной поверхностной силы
В
Creo Flow Analysis модель VOF может включать эффекты поверхностного натяжения вдоль интерфейса на границе раздела каждой пары фаз. Принята модель поверхностного натяжения на основе модели непрерывной поверхностной силы (CFS) Брэкбилла и др. Этот метод рассматривает эффект поверхностного натяжения как дополнительную объемную силу, сконцентрированную в интерфейсе, а не как поверхностную силу. Для интерфейса свободной поверхности, приведенного на
рисунке 2.26, основная жидкость - это фаза q (жидкая фаза) и вторичная жидкость - это фаза p (обычно газовая фаза). В соответствии с моделью поверхностной силы континуума кривизна поверхности вычисляется на основе локальных градиентов в поверхности по нормали к интерфейсу. Пусть

- вектор, нормальный к поверхности, определенный как градиент доли объема основной жидкости α
q:
Кривизна интерфейса k, определяется в терминах дивергенции вектора нормали объекта:
уравнение 2.93
где

- величина вектора

.
Сила поверхностного натяжения выражается как объемная сила с помощью теоремы о дивергенции, что является дополнительной характеристикой источника, добавленной в уравнение моментов смеси.
уравнение 2.94
где σ
qp - коэффициент поверхностного натяжения между жидкостью q и жидкостью p. Для него существует единица измерения: Н/м.
Уравнение 2.94 допускает сглаженную суперпозицию сил около ячеек, в которых находится более двух фаз. Если в ячейке присутствуют только две фазы, это описывается следующими уравнениями:
уравнение 2.95
уравнение 2.96
• Включение силы поверхностного натяжения
Важность эффектов поверхностного натяжения определяется двумя безразмерными параметрами: числом Рейнольдса Re и капиллярным числом Ca или числом Рейнольдса и числом Вебера We:
Если Re << 1, интерес представляет капиллярное число:
уравнение 2.97
где U∞ - это скорость свободного потока. Эффектами поверхностного натяжения можно пренебречь, если Ca >> 1, поскольку сила поверхностного натяжения слишком мала.
Если Re >> 1, интерес представляет число Вебера:
уравнение 2.98
где L - это характерная длина. Эффектами поверхностного натяжения можно также пренебречь, если We >> 1, а сила инерции намного больше, чем сила поверхностного натяжения.
Адгезия стенки (угол контакта)
Модель объема жидкости (VOF) позволяет задать угол прилипания к стенке во взаимодействии с моделью поверхностного натяжения. В соответствии с моделью Брэкбилла и др., вместо приложения этого граничного условия непосредственно к стенке используется угол контакта между жидкостью и стенкой у интерфейса, чтобы скорректировать нормаль к поверхности в ячейках около стенки. Это так называемое динамическое граничное условие приводит к корректировке кривизны поверхности около стенки.
Если θ - это угол контакта интерфейса свободной поверхности у стенки, как показано на
рисунке 2.26, то вектор нормали объекта в ячейке рядом со стенкой вычисляется следующим образом:
уравнение 2.99
где
| Вектор нормали объекта у стенки |
| Вектор касательной объекта у стенки |
Затем расчетная скорость нормали объекта

используется для определения локальной кривизны поверхности:
уравнение 2.93, а потом - силы поверхностного натяжения:
уравнение 2.94 или
уравнение 2.95.
 - вектор, нормальный к поверхности, определенный как градиент доли объема основной жидкости αq:
- вектор, нормальный к поверхности, определенный как градиент доли объема основной жидкости αq: - вектор, нормальный к поверхности, определенный как градиент доли объема основной жидкости αq:
- вектор, нормальный к поверхности, определенный как градиент доли объема основной жидкости αq:


 - величина вектора
- величина вектора 

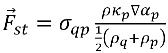
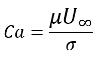

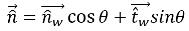


 используется для определения локальной кривизны поверхности:
используется для определения локальной кривизны поверхности: