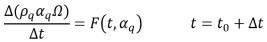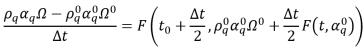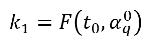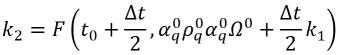Обсуждение численных расчетов
В однородных многофазных моделях без рассмотрения скольжения скорости не требуется специальный подход для решения уравнений импульса для смеси и формулировки теплового потока через границу объема. Это вызвано тем, что данные уравнения совпадают с уравнениями, которые управляют переменной плотностью однофазных потоков. Этот раздел посвящен построению уравнения поправок к давлению и обработке уравнений фазовых объемных долей, в особенности - схем разрешения интерфейса в модели VOF.
Уравнение непрерывности объема
Чтобы удовлетворить ограничение непрерывности и обеспечить числовую устойчивость, уравнение поправок к давлению строится на основе непрерывности суммарного объема вместо непрерывности массы. Когда вы делите
уравнение 2.57 для непрерывности/объемной доли q
-й фазы на эталонную плотность фазы, ρ
rq, и комбинируете все фазы вместе, вы получаете уравнение непрерывности суммарного объема, которое удовлетворяет закону сохранения массы:
уравнение 2.135
где эталонная плотность фазы обычно задается как плотность фазы, ρrq = ρq
Вводя величину Ω как объем расчетной ячейки и интегрируя
уравнение 2.135 по контрольному объему, получим дискретные алгебраические уравнения:
уравнение 2.136
Используя тот же подход, как и в решателе для единственной фазы на основе давления, который описан в численных расчетах, и предполагая следующее:
уравнение 2.137
уравнение 2.138
можно перекомпоновать
уравнение 2.136 как следующее уравнение для поправок:
уравнение 2.139
Здесь * и ’ представляют старые значения и исправления.
Δt | шаг времени |
Ae | область на грани e |
| объемный поток |
Следуя тому же подходу, как в однофазном решателе на основе давления, применим алгоритмы типа SIMPLE (Simple, SimpleC и SimpleS), чтобы связать поправки к скорости и давлению и получить уравнение коррекции давления для многофазных потоков:
уравнение 2.140
где
Anb | коэффициент связи |
Sp | линеаризовавший член |
Уравнения объемной доли фазы
Транспорт объемной доли фазы управляется сохранением массы фазы. Т. к. сохранение суммарного объема применятся при формулировке уравнения поправок к давлению, фактические уравнения, решенные для объемных долей фаз, также записываются в виде сохранения объема для числовой согласованности:
уравнение 2.141
Обычно для системы n фаз решаются только (n–1) уравнений, тогда как n-ю фазу получают из физического ограничения:
уравнение 2.142
Согласно методу дискретизации, интегральная форма
уравнения 2.141 имеет следующий вид:
уравнение 2.143
Как задано в уравнениях сохранения импульса, энергии и суммарного объема, пространственные и временные схемы дискретизации крайне важны для численной точности. Для уравнений объемных долей в дополнение к стандартным неявным временным схемам обычной практикой является использование явных временных решений вместе с высокоточными схемами со схемами переноса вещества для более точного описания интерфейсов в моделях VOF. В этом разделе подробно описаны и неявные, и явные формулировки VOF.
• Неявная формулировка VOF
В неявной формулировке VOF дискретизированное уравнение объемной доли фазы имеет следующее общее выражение:
уравнение 2.144
В этом уравнении объемная доля фазы α
q на текущем временном шаге является функцией других количественных значений на текущем временном шаге. Таким образом, в качестве уравнений для поправок для импульса, энергии и давления дискретизированное
уравнение 2.144 для объемной доли решается итерациями на каждом временном шаге. В
Creo Flow Analysis принятая неявная формулировка выглядит в итоге следующим образом:
◦ Схемы переноса вещества - объемный тепловой поток
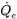
рассчитывается на основе поля потока на текущем временном шаге. Значение для фазы α
q,e выражается через значения в центре ячейки α
q,P, α
q,E и градиенты (
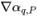
,
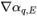
) соседних ячеек P и E. Как в пассивном скалярном уравнении, схемы переноса вещества имеют общую форму:
уравнение 2.145
С использованием различных значений для параметров γ, βP и βE и схем вычисления градиентов объемных долей разработаны четыре схемы переноса для уравнений объемной доли: первого порядка против потока, второго порядка против потока, разницы в центре и высокого разрешения.
◦ Временные схемы - чтобы описать неявную временную схему, можно обобщить
уравнение 2.144 в следующем выражении:
уравнение 2.146
Переменные без верхнего индекса являются значениями на текущем временном шаге. Переменные с верхним индексом 0 или 00 показывают значения на предыдущих временных шагах.
Параметры β и βCN изменяются от 0 до 1 и определяют временные схемы. В частности, для дискретизации уравнений объемной доли фазы принимаются три временные схемы:
▪ Схема Эйлера первого порядка против потока: β = 0, βCN = 1
▪ Трехуровневая второго порядка: β = 0, βCN = 1
▪ Метод Кранка - Николсона: β = 0, βCN = 0.6 (по умолчанию)
• Явная формулировка VOF
Когда для решения уравнений VOF используется явная формулировка, объемные доли фазы на текущем временном шаге рассчитываются непосредственно на основе известных количеств с предыдущего шага. Поэтому в явной формулировке VOF не требуется итерационное решение
уравнения 2.144 на каждом временном шаге. Однако поскольку остальные транспортные уравнения решаются неявно, временной шаг, используемый для расчета объемной доли, обычно является меньшим, чем временной шаг, используемый для других транспортных уравнений. Для явной формулировки VOF должен быть определен внутренний временной шаг, который может вычисляться автоматически или для которого можно предоставить решение
Creo Flow Analysis.
С явной формулировкой дискретизированное уравнение объемной доли фазы формулируется так:
уравнение 2.147
где и перенос, и члены источников рассчитываются на основе известных количественных значений с предыдущего шага. Объемный поток
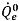
рассчитывается так же, как

в неявной формулировке. Объемная доля фазы
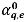
также может быть оценена с помощью одной из четырех схем переноса: первого порядка против потока, второго порядка против потока, разницы в центре и высокого разрешения.
Creo Flow Analysis предлагает следующие три алгоритма для явных схем временных решений:
• Явная схема Эйлера первого порядка - уравнение объемной доли дискретизируется следующим образом:
уравнение 2.148
• Схема Рунге - Кутты второго порядка - вводится следующая функция:
уравнение 2.149
уравнение 2.150
Тогда явная схема Рунге - Кутты второго порядка имеет вид:
уравнение 2.151
• Схема Рунге - Кутты четвертого порядка - для уравнения объемной доли фазы q явная схема Рунге - Кутты четвертого порядка имеет вид:
уравнение 2.152
где:
уравнение 2.153
уравнение 2.154
уравнение 2.155
уравнение 2.156
Для системы n фаз обычно решаются только (n-1) фазовых уравнений для объемных долей, а остающуюся долю получают из физического ограничения,
уравнение 2.142. Однако можно также решить все n уравнений для объемных долей и удовлетворить
уравнению 2.142, масштабируя каждую фазу с использованием суммы вычисленных объемных долей. В итерационном процессе это значение может быть больше или меньше 1.
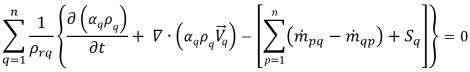
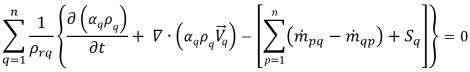
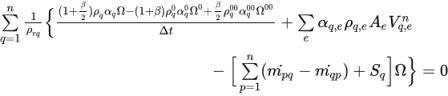
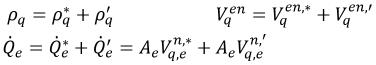
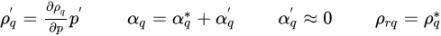
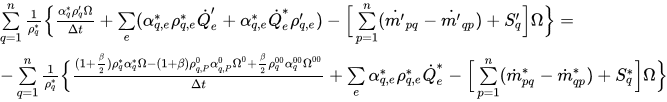

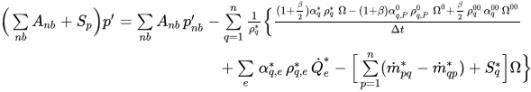

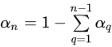


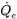 рассчитывается на основе поля потока на текущем временном шаге. Значение для фазы αq,e выражается через значения в центре ячейки αq,P, αq,E и градиенты (
рассчитывается на основе поля потока на текущем временном шаге. Значение для фазы αq,e выражается через значения в центре ячейки αq,P, αq,E и градиенты (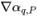 ,
, 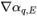 ) соседних ячеек P и E. Как в пассивном скалярном уравнении, схемы переноса вещества имеют общую форму:
) соседних ячеек P и E. Как в пассивном скалярном уравнении, схемы переноса вещества имеют общую форму: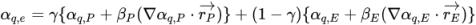

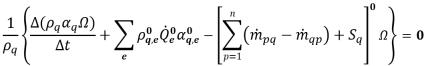
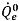 рассчитывается так же, как
рассчитывается так же, как  в неявной формулировке. Объемная доля фазы
в неявной формулировке. Объемная доля фазы 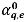 также может быть оценена с помощью одной из четырех схем переноса: первого порядка против потока, второго порядка против потока, разницы в центре и высокого разрешения.
также может быть оценена с помощью одной из четырех схем переноса: первого порядка против потока, второго порядка против потока, разницы в центре и высокого разрешения.