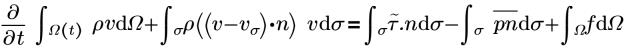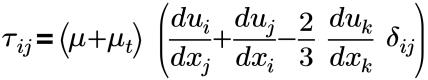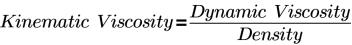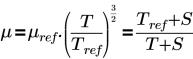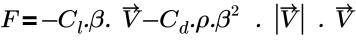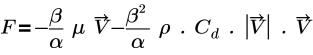흐름 모델
흐름(Flow) 모듈은 과도 나비어-스톡스 방정식
H.Ding, F.C. Visser, Y.Jiang, and M. Furmanczyk, "Demonstration and Validation of a 3-D CFD Simulation Tool Predicting Pump Performance and Cavitation for Industrial Applications," FEDSM2009-78256, 2009.을 사용하여 질량 보존과
운동량의 해를 구합니다.
RANS(레이놀즈의 평균 나비어-스톡스 방정식)의 적분 양식(보존)은 다음과 같습니다.
• 연속성
• 운동량
• 응력 텐서
여기서 각 항목은 다음을 나타냅니다.
τij | 유효한 전단 응력(분자+터뷸런스) |
f | 체적력 |
n | 서피스 수직 |
ρ | 정압(Pa) |
t | 시간 |
v | 유체 속도 |
vσ | 메쉬 속도 |
Ω(t) | 시간의 함수인 검사 체적 |
r | 평균 로컬 유체 밀도(kg/m3) |
σ | 검사 체적의 서피스 |
µ | 역학 점도(푸아즈 또는 Pa-s) |
µt | 터뷸런스 역학 점도 |
δij | 크로네커 델타(i=j인 경우 1, i≠j인 경우 0) |
점도 모델
• 일정 역학 점도(Constant Dynamic Viscosity) - 선택한 체적에서 유체
점도를 지정합니다. 역학 점도의 단위는 Pa-s 또는 N-s/m
2입니다.
역학 점도의 값은 Constant Dynamic Viscosity 선택 항목 아래의 상자에서 지정됩니다.
• 일정 동적 점도(Constant Kinematic Viscosity) - 선택한 체적에서 유체
점도를 지정합니다. 동적 점도의 단위는 m
2/s입니다. 동적 점도의 값은
Constant Kinematic Viscosity 선택 항목 아래의 상자에서 지정됩니다.
• 서덜랜드 법칙(Sutherland Law) - 선택한 체적에서 역학 점도(Pa-s)와 관련하여 유체
점도를 지정합니다. 방정식과 입력은 다음과 같습니다.
여기서 각 항목은 다음을 나타냅니다.
T | 온도(K) |
µref | 참조 온도에서의 점도(Pa-s) |
S | 서덜랜드 온도(K) |
|  T는 에너지 모듈이 활성 상태가 아닌 경우 입력해야 하는 유체 온도(K)입니다. |
서덜랜드 법칙은 온도의 함수로 이상 기체의 점도를 계산하는 데 사용됩니다.
Sutherland, W. (1893), "The viscosity of gases and molecular force," Philosophical Magazine, S. 5, 36, pp. 507-531 (1893). 다음 표에는 선택한 기체에 대한 서덜랜드의 일정 온도 및 참조 온도가 나와 있습니다. 참고:
en.wikipedia.org/wiki/viscosity기체 | S (K) | Tref (K) | mref (Pa-s) |
공기 | 120 | 291.15 | 18.27 e-6 |
질소 | 111 | 300.55 | 17.81 e-6 |
산소 | 127 | 292.25 | 20.81 e-6 |
이산화탄소 | 240 | 293.15 | 14.8 e-6 |
일산화탄소 | 118 | 288.15 | 17.2 e-6 |
수소 | 72 | 293.85 | 8.76 e-6 |
암모니아 | 370 | 293.15 | 9.82 e-6 |
아황산가스 | 416 | 293.65 | 12.54 e-6 |
헬륨 | 79.4 | 273 | 19 e-6 |
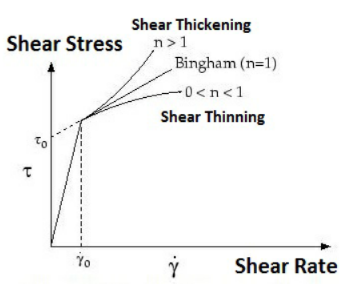
비뉴턴 점도 모델
비뉴턴 점도 모델은 다음과 같습니다.
• Herschel-Bulkley 모델
• Bingham 모델
이러한 모델은 비뉴턴 흐름 특성을 보이는 다양한 유형의 유체에 대해 적절한 점도를 제공합니다. Herschel-Bulkley 모델과 Bingham 모델은 다음과 같이 전단 응력과 전단 속도를 관련시킵니다.
여기서 각 항목은 다음을 나타냅니다.
e0 | 임계 전단 속도 |
k | 일치 지수 |
τ0 | 유체의 항복 응력 |
n | 거듭제곱 법칙 지수. Bingham 모델의 경우, n=1 |
|  전단 속도 0은 위 도표의 감마점과 동일합니다. |
저항 모델
저항 모델은 선택한 체적에서 저항을 설정하는 데 사용할 수 있는
흐름(Flow) 모듈 옵션입니다.
저항 모델에는 다음과 같은 두 개의 모델이 포함되어 있습니다.
• 압력 손실: 다음 방정식을 기반으로 합니다.
여기서 각 항목은 다음을 나타냅니다.
Cl | 선형 항력 계수(Pa-s/m2) |
Cd | 2차 항력 계수(1/m) |
β | 다공성 |
ρ | 밀도 |
• 다르시의 법칙: 다음 방정식을 기반으로 하는 모델입니다.
여기서 각 항목은 다음을 나타냅니다.
β | 다공성 |
α | 투자율 |
µ | 역학 점도 |
V | 속도 |
Cd | 2차 항력 계수(1/m) |
저항 방정식에 사용되는 속도는 로컬 속도입니다. 방정식에서 F는 힘/체적, 기압 경도(Dp/Dx) 또는 rg와 같이 N/m3 단위로 측정됩니다. 인터페이스를 지나는 압력 강하는 F를 유한 두께로 곱하여 계산됩니다. 다공성은 공통(Common) 모듈에서 설정됩니다.