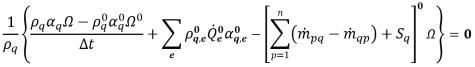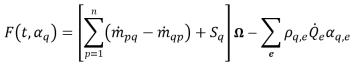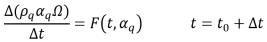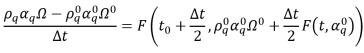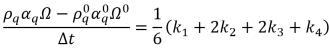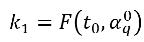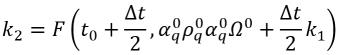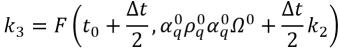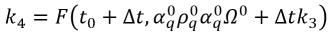数値に関する考慮事項
均一多相モデルにおいて、速度すべりを考慮しない場合、混合物運動量方程式と面の体積流束の式で特別な処理は必要ありません。これは、これらが可変密度の単相フローを支配する方程式と同じであるためです。このトピックでは、圧力補正式の作成と、相の体積分率の式、特に、VOF モデルにおける界面分解スキームの処理に重点を置いて説明します。
体積連続方程式
連続性の制約を満たして数値的な安定性を確保するため、質量連続性ではなく総体積連続性に基づいて圧力補正式が作成されています。q 番目の相の連続性/体積分率
式 2.57を相の基準密度ρ
rq で割って、すべての相を合わせると、質量保存の法則を満たす総体積の連続方程式が得られます。
式 2.135
ここで、相の基準密度は相の密度として設定される (ρrq = ρq) ことが一般的です
計算対象のセルの体積としてΩを使用し、
式 2.135を制御ボリューム上で積分すると、以下のような離散代数方程式ができます。
式 2.136
「数値」トピックで説明されている圧力ベースの単相ソルバーと同じアプローチを使用し、以下を仮定した場合、
式 2.137
式 2.138
式 2.136を以下のような補正式に再編成できます。
式 2.139
ここで、* と ' は以前の値と補正を表します。
圧力ベースの単相ソルバーと同じアプローチに従って、SIMPLE タイプのアルゴリズム (Simple、SimpleC、および SimpleS) を適用して、速度補正と圧力補正を結合することで、多相フローでの圧力補正式を求めます。
式 2.140
ここで、
相の体積分率の式
相の体積分率の輸送は相の質量保存によって支配されます。圧力補正式の作成では総体積保存が適用されるので、数値的整合性を確保するため、相の体積分率について計算される実際の式も体積保存の形式をとります。
式 2.141
通常、n 相の系では、(n-1) 個の式だけが計算され、n 番目の相は物理的な制約条件を使用して求められます。
式 2.142
離散化アプローチに従った場合、
式 2.141の積分形式は以下のようになります。
式 2.143
運動量、エネルギー、総体積の保存の式で示されているように、数値的な精度を確保するためには、空間と時間の離散化スキームが重要です。体積分率の式では、標準の陰的な時間スキームに加え、高解像度移流スキームで陽的な時間進行スキームを使用するのが一般的であり、これによって VOF モデル内の界面をさらに正確に取り込むことができます。このセクションでは、VOF の陰的解法と陽的解法について詳しく説明します。
• VOF の陰的解法
VOF の陰的解法では、相の体積分率の離散化式は以下の一般式を持ちます。
式 2.144
この式において、現在の時間ステップにおける相の体積分率α
q は、現在の時間ステップにおけるほかの量の関数です。したがって、運動量、エネルギー、圧力の補正式として、離散化体積分率
式 2.144が各時間ステップで反復的に計算されます。
Creo Flow Analysis で採用されている陰的解法は以下のように要約されます。
◦ 移流スキーム - 容積流束
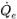
が現在の時間ステップにおけるフローフィールドに基づいて計算されます。隣接するセル P と E のセル中央の値α
q,P、α
q,E および勾配 (
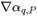
、
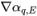
) を使用して面の値α
q,e が近似されます。パッシブスカラー式と同様に、移流スキームは以下の一般形式をとります。
式 2.145
パラメータγ、βP、およびβE に異なる値を使用し、体積分率の勾配を計算するスキームによって、体積分率の式に 1 次風上差分、2 次風上差分、中心差分、高解像度の 4 つの移流スキームが作成されます。
◦ 時間スキーム - 陰的時間スキームを表すため、以下の式で
式 2.144を一般化できます。
式 2.146
上付き文字がない変数は、現在の時間ステップにおける値です。上付き文字 0 または 00 が付いた変数は、前の時間ステップにおける値です。
パラメータβとβCN は 0 と 1 の間で変化し、これによって時間スキームが決まります。具体的には、相の体積分率の式の離散化では以下の 3 つの時間スキームが採用されています。
▪ オイラー 1 次風上: β = 0、βCN = 1
▪ 3 レベル 2 次: β = 0、βCN = 1
▪ クランク-ニコルソン法: β = 0、βCN = 0.6 (デフォルト)
• VOF の陽的解法
VOF 式の計算に陽的解法を使用した場合、現在の時間ステップにおける相の体積分率は、前の時間ステップからの既知の量に基づいて直接計算されます。したがって、VOF の陽的解法では各時間ステップ中に
式 2.144の反復計算を必要としません。ただし、残りの輸送方程式は陰的に計算されるので、体積分率の計算の時間ステップは、その他の輸送方程式の時間ステップよりも小さいことが一般的です。VOF の陽的解法ではサブ時間ステップを計算する必要があり、これは自動的に計算されるか、
Creo Flow Analysis でユーザーが指定できます。
陽的解法では、相の体積分率の離散化式は以下の式になります。
式 2.147
ここでは、移流項とソース項の両方が、前の時間ステップからの既知の量に基づいて計算されます。体積流束
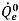
は陰的解法での
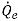
と同じ方法で計算されます。1 次風上差分、2 次風上差分、中心差分、高解像度の 4 つの移流スキームのいずれかを使用して、面の体積分率
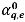
も推定できます。
Creo Flow Analysis は陽的時間進行スキーム用に以下の 3 つのアルゴリズムを提供しています。
• オイラー 1 次陽的 - 体積分率の式が以下のように離散化されます。
式 2.148
• ルンゲ-クッタ 2 次 - 以下の関数を導入しています。
式 2.149
式 2.150
その結果、2 次ルンゲ-クッタ陽的スキームは以下の形式をとります。
式 2.151
• ルンゲ-クッタ 4 次 - 相 q の体積分率の式で、4 次ルンゲ-クッタ陽的スキームは以下の形式をとります。
式 2.152
ここで、
式 2.153
式 2.154
式 2.155
式 2.156
n 相の系では、通常は (n-1) 相の体積分率だけが計算され、残りの 1 つの相は物理的な制約条件、
式 2.142から求められます。ただし、n 相すべての体積分率の式を計算することもでき、
式 2.142は計算された総体積分率の合計を使用して各相のスケールを調整することによって満たされます。反復プロセスでは計算された総体積分率の合計が 1 より小さくなったり大きくなったりする場合があります。
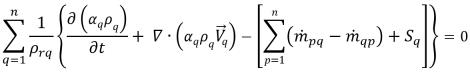
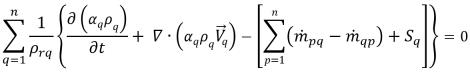
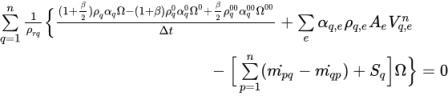
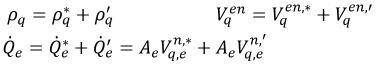
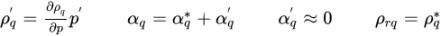
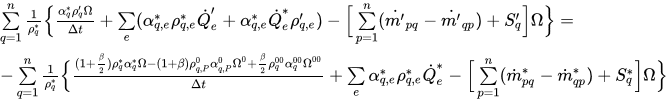
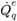
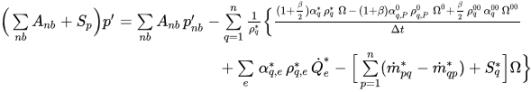
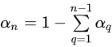
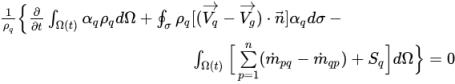
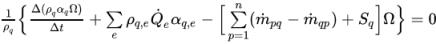
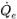 が現在の時間ステップにおけるフローフィールドに基づいて計算されます。隣接するセル P と E のセル中央の値αq,P、αq,E および勾配 (
が現在の時間ステップにおけるフローフィールドに基づいて計算されます。隣接するセル P と E のセル中央の値αq,P、αq,E および勾配 (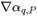 、
、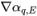 ) を使用して面の値αq,e が近似されます。パッシブスカラー式と同様に、移流スキームは以下の一般形式をとります。
) を使用して面の値αq,e が近似されます。パッシブスカラー式と同様に、移流スキームは以下の一般形式をとります。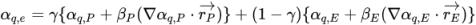
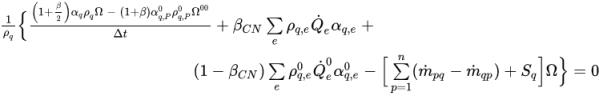
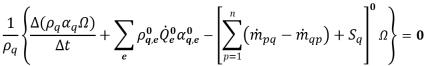
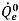 は陰的解法での
は陰的解法での 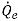 と同じ方法で計算されます。1 次風上差分、2 次風上差分、中心差分、高解像度の 4 つの移流スキームのいずれかを使用して、面の体積分率
と同じ方法で計算されます。1 次風上差分、2 次風上差分、中心差分、高解像度の 4 つの移流スキームのいずれかを使用して、面の体積分率 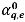 も推定できます。
も推定できます。