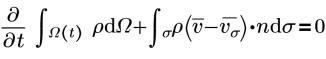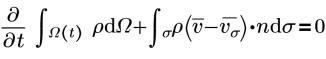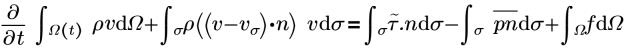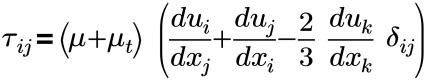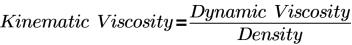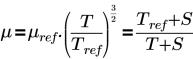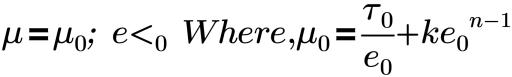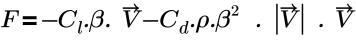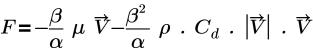フローモデル

質量および運動量保存のための「フロー」(Flow) モジュールの解法 (非定常 Navier-Stokes 方程式を使用) H.Ding、F.C. Visser、Y.Jiang、および M. Furmanczyk「Demonstration and Validation of a 3-D CFD Simulation Tool Predicting Pump Performance and Cavitation for Industrial Applications」FEDSM2009-78256、2009。

Reynold's Averaged Navier-Stokes 方程式 (RANS) の積分形式 (保存) は次のとおりです。

τij	有効なせん断応力 (分子 + 乱流)
f	ボディのフォース
n	サーフェス法線
ρ	静的圧力 (Pa)
t	時間
v	流体速度
vσ	メッシュ速度
Ω(t)	時間の関数として制御ボリューム
r	ローカル流体密度の平均 (kg/m3)
σ	制御ボリュームのサーフェス
µ	動粘度 (ポアズまたは Pa-s)
µt	乱流の動粘度
δij	クロネッカーのデルタ (i=j では =1、i≠j では =0)

• 「Constant Dynamic Viscosity」 - 選択した体積の流体の粘度を指定します。動粘度の単位は、Pa-s または N-s/m2 です。

動粘度の値は、「Constant Dynamic Viscosity」選択にあるボックスで指定します。

• 「Constant Kinematic Viscosity」 - 選択した体積の流体の粘度を指定します。キネマティック粘度の単位は m2/s です。キネマティック粘度の値は、「Constant Kinematic Viscosity」選択にあるボックスで指定します。

• 「Sutherland Law」 - 選択した体積の流体の粘度を、動粘度 (Pa-s) で指定します。方程式と入力は次のとおりです。

T	温度 (K)
µref	参照温度の粘度 (Pa-s)
S	サザランド温度 (K)

注記 T は、エネルギーモジュールがアクティブでない場合に、入力として必要とされる流体温度 (K) です。

サザランド則を使用して、理想気体の粘度を温度の関数として計算します。Sutherland, W. (1893), "The viscosity of gases and molecular force," Philosophical Magazine, S. 5, 36, pp. 507-531 (1893)。次の表に、選択した気体に対するサザランドの定数と参照温度を示します。参照: en.wikipedia.org/wiki/viscosity

気体	S (K)	Tref (K)	mref (Pa-s)
空気	120	291.15	18.27 e-6
窒素	111	300.55	17.81 e-6
酸素	127	292.25	20.81 e-6
二酸化炭素	240	293.15	14.8 e-6
一酸化炭素	118	288.15	17.2 e-6
水素	72	293.85	8.76 e-6
アンモニア	370	293.15	9.82 e-6
二酸化硫黄	416	293.65	12.54 e-6
ヘリウム	79.4	273	19 e-6

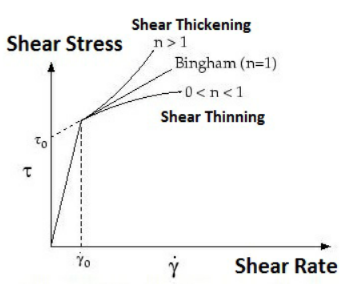
これらのモデルは、非ニュートンフローのプロパティを示すさまざまなタイプの流体に対して適切な粘度を提供します。Herschel-Bulkley モデルと Bingham モデルは、せん断応力とせん断率を次のように関連付けます。

e0	重要なせん断率
k	一貫性指標
τ0	流体の降伏応力
n	べき乗則の指数Bingham モデルの場合、n =1

注記せん断率 0 は、上のプロットのガンマ点と同じです。

「Resistance Model」は、選択した体積で抵抗を設定するために使用できるフローモジュールオプションです。「Resistance Model」には、次の 2 つのモデルが含まれています。

Cl	直線ドラッグ係数 (Pa-s/m2)
Cd	2 次ドラッグ係数 (1/m)
β	多孔性
ρ	密度

β	多孔性
α	透磁率
µ	動粘度
V	速度
Cd	2 次ドラッグ係数 (1/m)

抵抗方程式で使用される速度は、ローカル速度です。この方程式の F は、単位 N/m3 (荷重/体積など)、圧力勾配 (Dp/Dx)、または rg で測定されます。インタフェース全体の圧力損失は、F と有限厚を掛け合わせることで求められます。多孔性は「共通」(Common) モジュールで設定します。