Creo Flow Analysis > Preprocessing > Physik definieren > Turbulence > Physik > Turbulenzmodelle
  
Turbulenzmodelle
Sie können die effektive turbulente Viskosität in einem Flüssigkeitssystem auf Basis des Wirbelviskositätsmodells berechnen. Es gibt zwei Modelle im Wirbelviskositätsmodell:
• Standard-K-Epsilon-Modell
Das Standard-K-Epsilon-Modell ist ein Turbulenzmodell , das in Creo Flow Analysis verfügbar ist.
Die Formel für die turbulente kinetische Energie k lautet:
Die Formel für die turbulente Dissipationsrate ε lautet:
Dabei gilt:
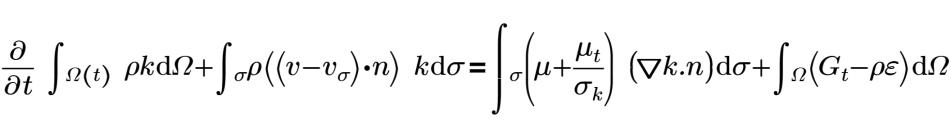
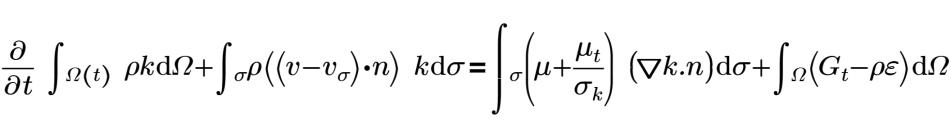
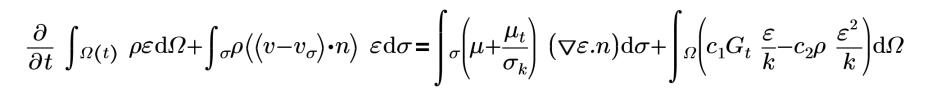
c1=1.44
Konstanten C1
c2=1.92
Konstanten C2
σk=1
Turbulente kinetische Energie, Prandtl-Zahl
σz=1
Turbulente Dissipationsrate, Prandtl-Zahl
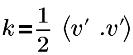Turbulente kinetische Energie
v’
Turbulente Schwankungsgeschwindigkeit
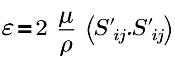Turbulente Energiedissipationsrate
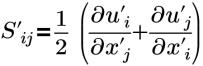Dehnungstensor
u’i(i=1,2,3)
Komponenten der turbulenten Schwankungsgeschwindigkeit
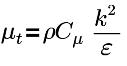Turbulente Viskosität, mit Cμ=0.09 und E=9.793
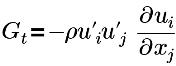Turbulenzgenerierungsterm
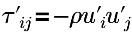Turbulenz, Reynolds-Spannung
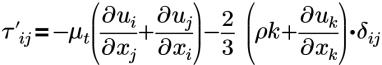Boussinesq-Näherung an Reynolds-Spannung
Referenzen: Launder, B.E. & Spalding, D.B. (1974) "The numerical computation of turbulent flows", Computer Methods, Applied Mechanics and Engineering, Vol. 3, S. 269-289
• RNG-K-Epsilon-Modell (Renormalization Group)
Das RNG-K-Epsilon-Modell (Renormalization Group) ist ein Turbulenzmodell, das in Creo Flow Analysis verfügbar ist. Dieses Modell ähnelt dem Standard-K-Epilson-Modell, jedoch mit einem Ausdruck, der zwei neue Konstanten umfasst. Diese werden verwendet, um den C2-RNG-Term in der Gleichung unten zu ändern:
Dabei gilt:
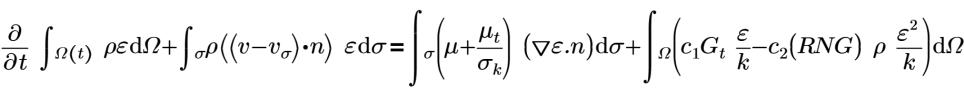
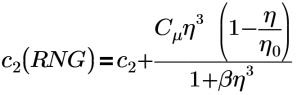
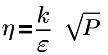
η0=4.38
RNG-Konstante (hartcodierte Konstante in Flow Analysis)
β=1.92
RNG-Konstante (hartcodierte Konstante in Flow Analysis)
P
Lokaler Druck
c1=1.44
Konstanten C1
c2=1.92
Konstanten C2
σk=1
Turbulente kinetische Energie, Prandtl-Zahl
σz=1
Turbulente Dissipationsrate, Prandtl-Zahl
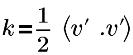Turbulente kinetische Energie
v’
Turbulente Schwankungsgeschwindigkeit
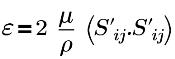Turbulente Energiedissipationsrate
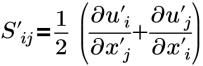Dehnungstensor
u’i(i=1,2,3)
Komponenten der turbulenten Schwankungsgeschwindigkeit
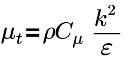Turbulente Viskosität, mit Cμ=0.09
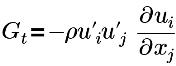Turbulenzgenerierungsterm
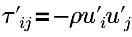Turbulenz, Reynolds-Spannung
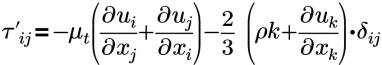Boussinesq-Näherung an Reynolds-Spannung
Referenzen: Yakhot, V., Orszag, S.A., Thangam, S., Gatski, T.B. & Speziale, C.G. (1992), "Development of turbulence models for shear flows by a double expansion technique", Phys. of Fluids A, Vol. 4, No. 7, S. 1510-1520