|
Type d'analyse :
|
Modale
|
|
Type de modèle :
|
Déformation plane 2D
|
|
Comparaison :
|
Résultats théoriques
|
|
Référence :
|
Roark, R.J. et Young, W.C. Formulas for Stress and Strain. NY : McGraw-Hill Book Co. 1982. pp.576578.
|
|
Description :
|
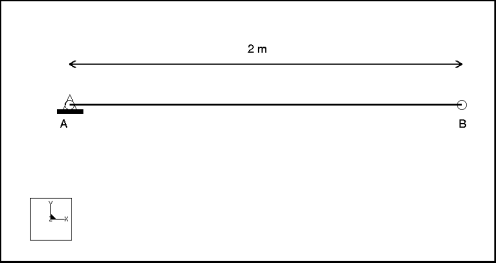
Trouvez la fréquence fondamentale d'une plaque encastrée modélisée en tant que modèle en déformation plane.
|

Type d'élément : | coque 2D (1) | |
Unités : | MKS | |
Cotes : | largeur : 2 épaisseur : 0,01 | |
Propriétés des matériaux : | Masse volumique : 7850 Coût par unité de masse : 0 Module de Young : 2e11 | Coefficient de Poisson : 0,3 Dilatation thermique : 0 Conductivité : 0 |
Restriction : | placé sur le point A : fixe dans l'ensemble des DDL | |
Théorie | Structure | % de différence | |
Fréquence fondamentale (Hz) (mode=1) | 2,1393 | 2.1374 | 0,08 % |
% de convergence : 0,4 % sur fréquence | P max. : 4 | Nbre d'équations : 12 | |
Type d'analyse : | Modale |
Type de modèle : | Contrainte plane 2D |
Comparaison : | Résultats théoriques |
Référence : | Roark, R.J. et Young, W.C. Formulas for Stress and Strain. NY : McGraw-Hill Book Co. 1982. pp.576578. |
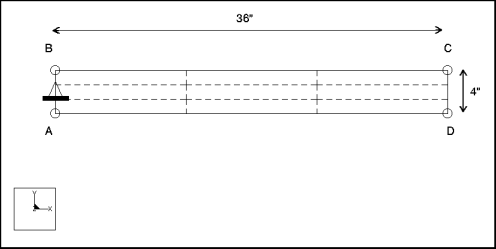
Description : | Trouvez la fréquence fondamentale de la vibration latérale d'une plaque encastrée. |
Type d'élément : | plaque 2D (1) | |
Unités : | IPS | |
Cotes : | longueur : 36 largeur : 4 épaisseur : 0.1 | |
Propriétés des matériaux : | Masse volumique : 7.28e4 Coût par unité de masse : 0 Module de Young : 3e7 | Coefficient de Poisson : 0,3 Dilatation thermique : 0 Conductivité : 0 |
Restriction : | placé sur l'arête A-B : fixe dans TransX et TransY | |
Théorie | Structure | % de différence | |
Fréquence fondamentale (Hz) (mode=1) | 101,326 | 100.988 | 0,33 % |
% de convergence : 0,4 % sur fréquence | P max. : 6 | Nbre d'équations : 42 | |
Type d'analyse : | Modale |
Type de modèle : | Déformation plane 2D |
Comparaison : | Résultats théoriques |
Référence : | Roark, R.J. et Young, W.C. Formulas for Stress and Strain, NY:McGraw-Hill Book Co. 1982. pp.576578. |
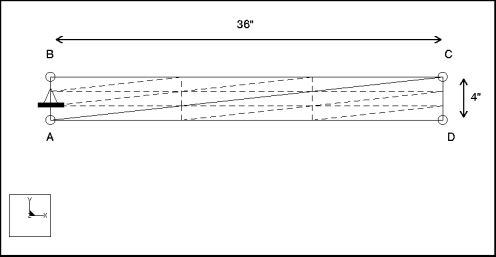
Description : | Trouvez la fréquence fondamentale d'une plaque encastrée modélisée en tant que modèle en déformation plane. |
Type d'élément : | solide 2D (2) | |
Unités : | IPS | |
Cotes : | longueur : 36 largeur : 4 | |
Propriétés des matériaux : | Masse volumique : 7.28e4 Coût par unité de masse : 0 Module de Young : 3e7 | Coefficient de Poisson : 0,3 Dilatation thermique : 0 Conductivité : 0 |
Restriction : | placé sur l'arête A-B : fixe dans TransX, TransY et RotZ | |
Théorie | Structure | % de différence | |
Fréquence fondamentale (Hz) (mode=1) | 106,219 | 106.604 | 0.36% |
% de convergence : 0.8% sur fréquence | P max. : 6 | Nbre d'équations : 42 | |
Type d'analyse : | Modale |
Type de modèle : | 2D axisymétrique |
Comparaison : | ANSYS n° 67 |
Référence : | Timoshenko, S. et Young, D.H. Vibration Problems in Engineering. 3ème éd. NY: D. Van Nostrand Co., Inc. 1955. p. 425, Art. 68 |
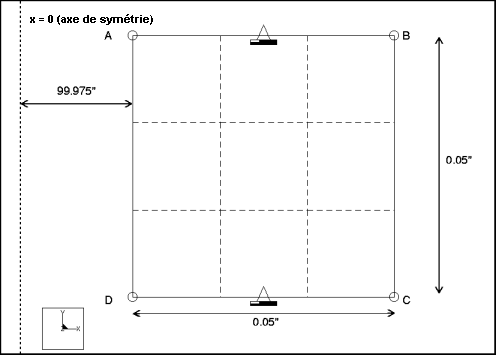
Description : | Trouvez la fréquence fondamentale de la vibration radiale d'un anneau modélisé axisymétriquement. |
Type d'élément : | solide 2D (1) | |
Unités : | IPS | |
Cotes : | rayon interne : 99,975 rayon externe : 100,025 hauteur : 0,05 | |
Propriétés des matériaux : | Masse volumique : 7,3e4 Coût par unité de masse : 0 Module de Young : 3e7 | Coefficient de Poisson : 0 Dilatation thermique : 0 Conductivité : 0 |
Restrictions : | placé sur l'arête A-B :fixe dans TransY et RotZ placé sur l'arête C-D :fixe dans TransY et RotZ | |
Théorie | ANSYS | Structure | % de différence | |
Fréquence radiale (Hz) (mode=1) | 322,64 | 322,64 | 322,64 | 0,0 % |
% de convergence : 0,0 % sur fréquence | P max. : 2 | Nbre d'équations : 10 | ||
Type d'analyse : | Modale |
Type de modèle : | 3D |
Comparaison : | Résultats théoriques |
Référence : | Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity. 4ème éd. NY : Dover Publications. 1944. p. 452, Art. 293b. |
Description : | Déterminez la première et la seconde fréquences modales pour la vibration radiale d'une couronne modélisée en tant que modèle un quart. |
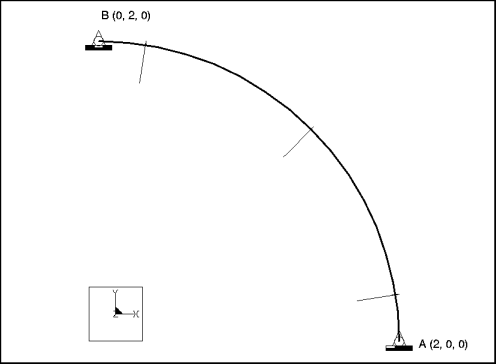
Type d'élément : | poutre (1) | |
Unités : | IPS | |
Cotes : | rayon : 2 | |
Propriétés des poutres : | Aire : 0,01 IYY : 1e3 Cisaillement FY : 0,83333 CY : 1 | J : 1,008e3 IZZ : 8,33e6 Cisaillement FZ : 0,83333 CZ : 1 |
Propriétés des matériaux : | Masse volumique : 7.28e4 Coût par unité de masse : 0 Module de Young : 3e7 | Coefficient de Poisson : 0,3 Dilatation thermique : 0 Conductivité : 0 |
Restrictions : | placé sur le point A : fixe dans tous les DDL sauf TransX placé sur le point B : fixe dans l'ensemble des DDL sauf TransY | |
Théorie | Structure | % de différence | |
Fréquence (Hz) mode 1 | 625,65 | 624,43 | 0,19 % |
Fréquence (Hz) mode 2 | 3393,06 | 3369,13 | 0,70 % |
% de convergence : 0,0 % sur fréquence | P max. : 9 | Nbre d'équations : 50 | |
Type d'analyse : | Modale |
Type de modèle : | 3D |
Comparaison : | ANSYS n° 62 |
Référence : | Timoshenko, S. et Young, D.H. Vibration Problems in Engineering. 3ème éd. NY : D. Van Nostrand Co., Inc. 1955. p. 392, Art. 62. |
Description : | Trouvez la fréquence fondamentale de la vibration latérale d'une plaque en forme de coin encastrée. |
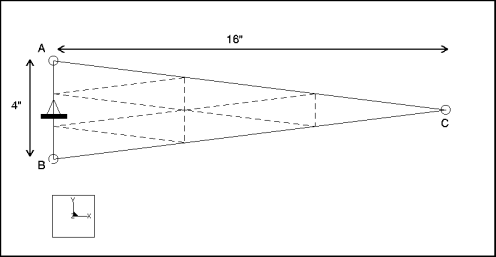
Type d'élément : | coque (1) | |
Unités : | IPS | |
Cotes : | longueur : 16 largeur : 4 épaisseur : 1 | |
Propriétés des matériaux : | Masse volumique : 7.28e4 Coût par unité de masse : 0 Module de Young : 3e7 | Coefficient de Poisson : 0 Dilatation thermique : 0 Conductivité : 0 |
Restriction : | placé sur l'arête A-B : fixe dans l'ensemble des DDL | |
Théorie | ANSYS | Structure | % de différence | |
Fréquence (Hz) (mode=1) | 259,16 | 260,99 | 259,15 | 0,004 % |
% de convergence : 0,0 % sur fréquence | P max. : 4 | Nbre d'équations : 60 | ||
Type d'analyse : | Modale |
Type de modèle : | 3D |
Comparaison : | Résultats théoriques |
Référence : | Roark, R.J. et Young, W.C. Formulas for Stress and Strain. NY : McGraw-Hill Co. 1982. p.576. |
Description : | Une coque cylindrique encastrée est modélisée en tant que demi-cylindre avec symétrie. Trouvez la fréquence fondamentale. |
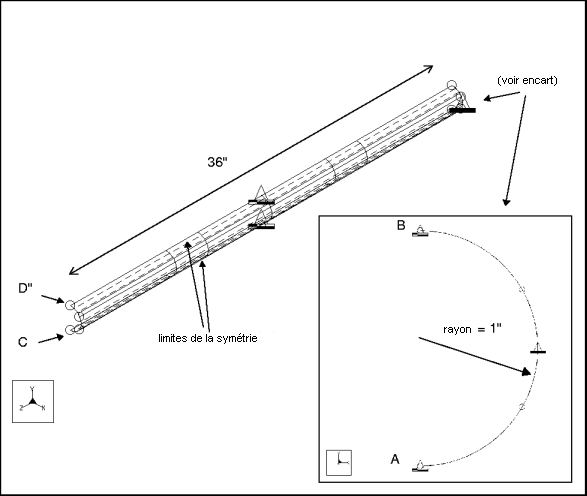
Type d'élément : | coque (3) | |
Unités : | IPS | |
Cotes : | longueur : 36 rayon : 1 épaisseur : 0.1 | |
Propriétés des matériaux : | Masse volumique : 7.28e4 Coût par unité de masse : 0 Module de Young : 3e7 | Coefficient de Poisson : 0,3 Dilatation thermique : 0 Conductivité : 0 |
Restriction : | placé sur l'arête A-B : fixe dans l'ensemble des DDL placé sur la face A-C, B-D : fixe dans TransX, RotY et RotZ | |
Théorie | Structure | % de différence | |
Fréquence (Hz) (mode=1) | 62,05 | 62.125 | 0.12% |
% de convergence : 0,4 % sur fréquence | P max. : 6 | Nbre d'équations : 180 | |
Type d'analyse : | Modale |
Type de modèle : | 3D |
Comparaison : | ANSYS n° 62 |
Référence : | Timoshenko, S. et Young, D.H. Vibration Problems in Engineering. 3ème éd. NY : D. Van Nostrand Co., Inc. 1955. p. 392, Art. 62 |
Description : | Trouvez la fréquence fondamentale de la vibration latérale d'une plaque en forme de coin encastrée. |
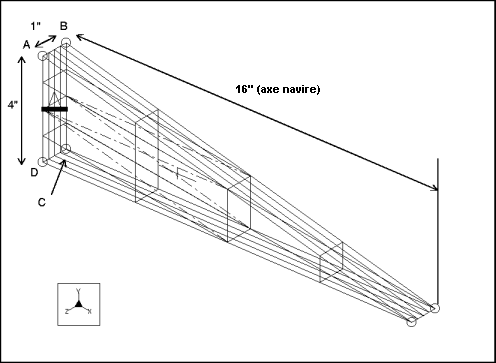
Type d'élément : | solide (1) | |
Unités : | IPS | |
Cotes : | longueur : 16 largeur : 4 profondeur : 1 | |
Propriétés des matériaux : | Masse volumique : 7,28e–4 Coût par unité de masse : 0 Module de Young : 3e7 | Coefficient de Poisson : 0 Dilatation thermique : 0 Conductivité : 0 |
Restriction : | placé sur la face A-B-C-D : fixe dans l'ensemble des DDL | |
Théorie | ANSYS | Structure | % de différence | |
Fréquence fondamentale (Hz) (mode=1) | 259,16 | 260,99 | 259.24 | 0,03 % |
% de convergence : 0,0 % sur fréquence | P max. : 4 | Nbre d'équations : 72 | ||
Type d'analyse : | Modale |
Type de modèle : | 3D |
Référence : | NAFEMS, SBNFA (Novembre 1987), Test 1. |
Description : | Déterminez les fréquences modales (de la première à la huitième) pour la vibration en plan d'une croix avec une articulation pivot aux points A, B, C et D. |
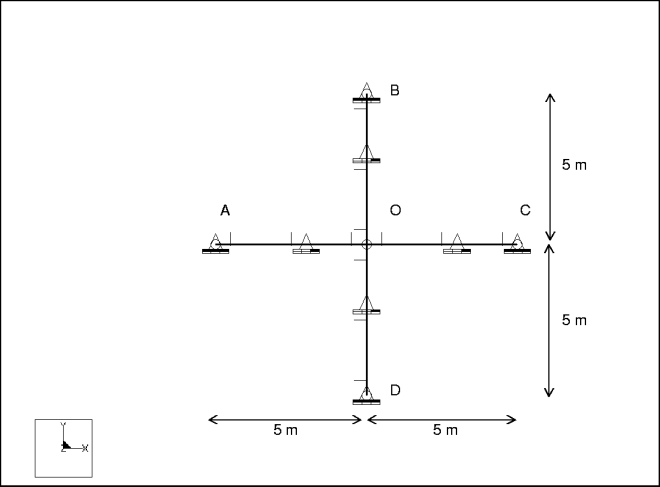
Type d'élément : | poutre (4) | |
Unités : | NMS | |
Cotes : | longueur : 5 | |
Propriétés des poutres : | Aire : 0,015625 IYY : 2,0345e–5 Cisaillement FY : 0,83333 CY : 0,0625 | J : 4,069e–5 IZZ : 2,0345e–5 Cisaillement FZ : 0,83333 CZ : 0,0625 |
Propriétés des matériaux : | Masse volumique : 8000 Coût par unité de masse : 0 Module de Young : 2e11 | Coefficient de Poisson : 0,3 Dilatation thermique : 0 Conductivité : 0 |
Restrictions : | placé sur les points A, B, C, D : fixe dans TransX, TransY et TransZ placé sur les poutres A-O, B-O, C-O, D-O : fixe dans TransZ | |
Théorie | Structure | % de différence | |
Fréquence (Hz) mode 1 | 11,336 | 11.312 | 0.211% |
Fréquence (Hz) mode 2 et 3 | 17,709 | 17.636 | 0.412% |
Fréquence (Hz) mode 4 | 17,709 | 17.636 | 0.412% |
Fréquence (Hz) mode 5 | 45,345 | 45,155 | 0.419% |
Fréquence (Hz) mode 6 et 7 | 57,390 | 56,692 | 1.216% |
Fréquence (Hz) mode 8 | 57,390 | 57.001 | 0.677% |
% de convergence : 3,4 % sur fréquence | P max. : 8 | Nbre d'équations : 157 | |
Type d'analyse : | Modale |
Type de modèle : | 3D |
Référence : | NAFEMS, SBNFA (Novembre 1987), Test 53. |
Description : | Déterminez les fréquences modales (de la première à la cinquième) pour la vibration axisymétrique d'une plaque annulaire. |
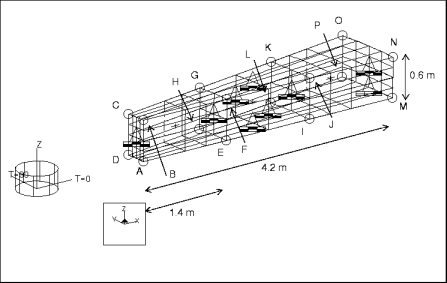
Type d'élément : | solide (3) | |
Unités : | NMS | |
Cotes : | rayon interne : 1,8 rayon externe : 6 hauteur : 0,6 | |
Propriétés des matériaux : | Masse volumique : 8000 Coût par unité de masse : 0 Module de Young : 2e11 | Coefficient de Poisson : 0,3 Dilatation thermique : 0 Conductivité : 0 |
Restrictions : | Emplacement | Degrés de liberté |
restriction1 | placé sur les surfaces ABCD, BCNO, ADMP, ABMN, CDPO, MNOP | fixe dans TransT, RotR et RotZ |
placé sur la courbe MP | fixe dans TransZ |
Théorie | Structure | % de différence | |
Fréquence modale (Hz) 1 | 18,583 | 18.550 | 0,17 % |
Fréquence modale (Hz) 2 | 140,15 | 138,22 | 1.37% |
Fréquence modale (Hz) 3 | 224,16 | 224,16 | 0 % |
Fréquence modale (Hz) 4 | 358,29 | 355,80 | 0,7 % |
Fréquence modale (Hz) 5 | 629,19 | 620,43 | 1,4 % |
% de convergence : 1,3 % de la fréquence | P max. : 9 | Nbre d'équations : 1094 | |