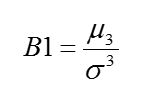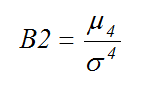幾何累積分佈
Creo Parametric Tolerance Analysis Extension powered by CETOL Technology 可圖示刻度動差的所有分佈。所用的動差為平均數、標準差、偏態和峰度。刻度動差是利用幾何累積分佈的中央動差 (接近平均數的動差) 計算得出的。
平均數
分佈平均數代表樣本群的平均值 (或正常值)。
Μ = 分佈圖平均
標準差
標準差 (σ) 是分佈圖分散程度的指標。它是第二階中央動差 (變異數) 的平方根:
其中:
μ2 = 第二階中央動差,變異數
偏態
偏態是分佈圖對稱程度的指標。偏態如為 0,表示分佈圖完全對稱。偏態與第三階中央動差有關。由於 Creo Tolerance Analysis 的所有分佈圖都應該是對稱的,因此偏態值一律為零。
其中:
μ3 = 第三階中央動差
峰度
峰度是分佈圖峰值的指標,或是意思完全相反的分佈尾重。峰度與第四階中央動差有關。在 Creo Tolerance Analysis powered by CETOL Technology 中,峰度標示為 B2 (Beta 2)。
其中:
μ4 = 第四階中央動差