了解疲劳分析
本文档提供了有关疲劳的背景信息并说明了 Creo Simulate 疲劳分析中使用的方法。涵盖的主题如下:
• 应变循环
包括平均残余应力的作用、磁滞回线捕获以及雨流循环计数。
• 影响疲劳寿命的因素
包括元件尺寸、载荷类型、表面粗糙度、表面处理 (即,机械处理、电镀和热处理) 以及表面处理对持久极限的影响。
与 Creo Simulate 疲劳分析集成的求解器技术由 nCode International 提供。疲劳分析需要 PTC 发放的 Fatigue Advisor 许可证。
疲劳历史
绝大多数元件设计所涉及的零件都会受到变动载荷或循环载荷的影响。此类载荷会引起脉动应力或循环应力,这些应力经常会通过疲劳导致零件失效。在所有结构性失效中,约有 95% 的失效是通过疲劳机制产生。
由于以下原因,在疲劳过程中形成的损伤是累积性的并且通常是不可恢复的:
• 要在疲劳过程中检测材料行为中的任何渐进性变化几乎是不可能的,因此失效通常是在没有任何预兆的情况下发生。
• 消除了疲劳应力的停用期不会导致任何明显的修复或恢复。
众所周知,大幅度地反复来回折弯木材或金属会使它们折断。但是,同时我们也发现即使应力幅度表面上完全处于材料的弹性范围内,通过反复施加应力也可以使材料发生破裂。当铁路轮轴的疲劳失效在 19 世纪中期成为普遍问题时,这引起了人们对循环载荷作用的注意。这是第一次让多个相似元件在远低于单调拉伸屈服应力的应力等级下承受数百万次循环的应力作用。从 1852 年到 1870 年期间,德国铁路工程师 August Wöhler 计划并实施了首次系统性的疲劳调查。
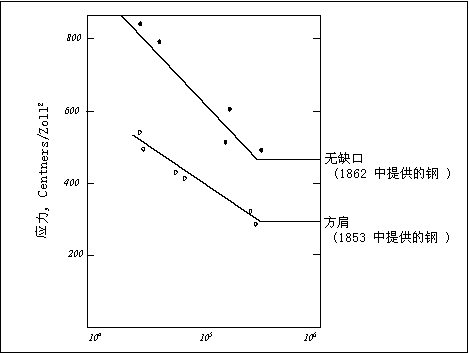
Wöhler 的一些调查数据针对的是 Krupp 车轴钢,并且根据名义应力 (S) 与疲劳失效周期数 (N) 的关系绘制了大家所知道的应力疲劳周期图。时至今日,我们仍然称此类图上的每条曲线为 Wöhler 线。
注意:1 centner = 50 kg, 1 zoll = 1 inch, 1 centner/zoll2 ~ 0.75 MPa
大约在同一时期,其他工程师也开始从事研究桥梁、船舶设备和发电机中与脉动载荷关联的的疲劳失效问题。在 20 世纪初期,人们把更多精力放在了解疲劳过程的机制上,而不是仅仅放在观察其结果上。此类活动最后在 50 年代的后期和 60 年代的前期导致了两种方法的发展,一个基于线弹性断裂力学 (LEFM),用于解释裂缝如何传播,一个基于所谓的 Coffin-Manson 局部应变方法学,用于解释裂缝引发。了解这些之后,现代的设计师和工程师已经能够在不仅仅依赖试验的情况下创造出抗疲劳性更强的元件。从实用的角度来看,这已成为更具有经济效益的方法。
疲劳的物理性质
自 1830 年以来,人们已认识到,对于被施加重复性载荷或脉动载荷的金属,即使其所承受的应力等级低于在施加单次相同载荷时导致疲劳失效所需的应力等级,该金属也会发生疲劳失效。
下图显示了一个在均衡的正弦态变化力作用下的简单元件。经过一段时间后,在孔的圆周面上开始出现一条裂缝。此裂缝随后会通过元件传播,直到剩余的完好部分不能承受施加的应力而使元件发生疲劳失效为止。
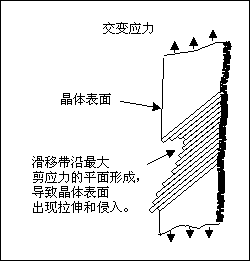
裂缝的物理发展通常分为两个单独阶段。它们指裂缝引发阶段 (阶段 I) 和裂缝生长阶段 (阶段 II)。疲劳裂缝通过释放剪应变能引发。下图显示了剪应力如何导致沿滑移面的局部塑性变形。由于载荷是呈正弦态循环,因此滑移面会象一副纸牌那样来回移动,从而导致在晶体表面上出现小的拉伸和侵入。这些表面扰动的高度约为 1 至 10 微米,并且构成了初期的裂缝。
裂缝就是这样开始的,直至其到达晶界。此时,作用机制开始逐渐传递到临近的晶粒。
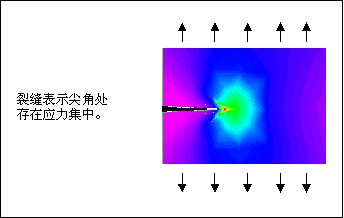
当裂缝扩展通过约 3 个晶粒时,会发现其传播方向发生了变化。阶段 I 中的裂缝沿着最大剪切面的方向增长,或者说沿着与载荷成 45° 的方向增长。在阶段 II 期间,疲劳的物理机制发生了变化。此时,裂缝已经大到足以形成一个几何应力集中点。如下图所示,在裂缝尖端形成了一个拉伸塑性区。在此阶段后,裂缝以垂直于所施加载荷的方向传播。
由于疲劳的物理机制分为两个阶段,因此分析方法通常也分为两个阶段。通常使用局部应变 (或 E-N) 方法分析阶段 I,而使用基于断裂力学的方法分析阶段 II。
因此,将两种方法结合使用可以进行完整的疲劳预测:
总寿命 = 引发期间寿命 + 传播裂缝直至疲劳失效期间的寿命
但是,大多数工程元件将大部分时间花费在两个阶段中的一个阶段上。这种情况下,通常仅适当地考虑一个阶段。例如,在多数地面车辆的设计中,车辆寿命通常取决于引发阶段的时间。元件具有比较大的刚性,材料则具有相当大的脆性。一旦引发裂缝,就会在较短的时间内传播裂缝而导致疲劳失效。
相反,许多航空应用领域使用由延展性很强的材料制造而成的挠性元件。这种情况下,裂缝的传播速度会较慢,因此断裂力学的方法通常更加适用。
在早期,疲劳的物理性质并非广为人知。因此,August Wöhler 对疲劳分析采取了更加实用的观点。他所开发的方法已成为人所共知的名义应力 (或 S-N) 疲劳分析。此方法不区分阶段 I 和 II 的裂缝增长方法,而是使名义应力范围与完成疲劳失效所需的时间相关联。
尽管 S-N 分析方法在基于试验的疲劳分析中仍被广泛利用,但它对于 CAE 应用程序有一个较大的缺点。疲劳引发是由局部塑性应变驱动的,但 S-N 分析使用弹性应力作为输入。因此,S-N 分析不适于对包含局部塑性区的元件进行 CAE 分析。因此,局部应变 (或 E-N) 方法更适于普遍应用。Creo Simulate 疲劳分析使用 E-N 方法。
E-N 方法
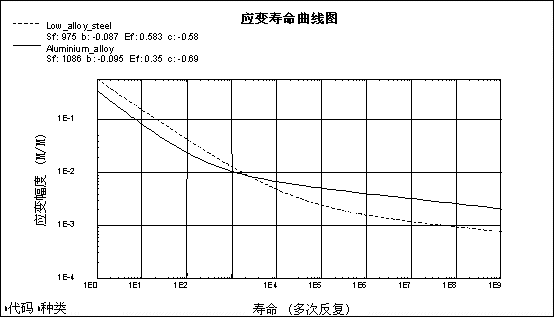
在疲劳试验中,不同材料类型的沙漏形试样受到各种类型的循环载荷作用,例如小规模的折弯、扭转、拉伸和压缩。E-N 方法使用这些试验来测量疲劳寿命。将针对应变 (E) 与疲劳失效周期数 (N) 的关系在 E-N 图上绘制结果。下面例示了一个低合金钢和铝合金的典型 E-N 图。
Creo Simulate 使用一组通用的疲劳属性为低合金钢、非合金钢、铝合金和钛合金建模。这些通用属性已由 Baumel Jr. 和 Seeger 汇编并被称为“均质材料定律”。尽管从实用角度讲,不能期望它们提供精确的疲劳寿命,但它们非常适用于确定某元件是否有可能会遭受疲劳问题,以及在投产前是否需要进行更详细的分析。有关“均质材料定律”的详细信息,请参阅
Materials Science Monographs, 61, "Materials Data for Cyclic Loading, Supplement 1" (《材料科学专论》,61,“循环载荷的材料数据,附录 1”)。
以下论述涉及了疲劳理论中对于理解 Fatigue Advisor 如何测量疲劳十分关键的两个方面:
应变循环
在详细介绍 E-N 过程之前,先了解促进疲劳过程的三种不同类型的循环应变会很有帮助。下图和相关说明解释了每个单独类型。
第一个图通过正弦曲线形式说明了一个完全反向的应变循环。这是理想化的载荷条件,通常发生在以恒速运行且没有超载荷的旋转轴中。这也是大多数疲劳试验所使用的应变循环类型。对于此类循环,最大 (
 max
max) 和最小 (
 min
min) 应变大小相等但符号相反。通常将拉伸应变视为正,将压缩应变视为负。应变范围
 r
r 是在一次循环中最大应变和最小应变的代数差。
应变幅度
 a
a 是应变范围的一半。
 a
a =
 r/2
r/2 = (
 max
max –
 max
max) / 2
第二个图说明了更为常见的情况,其中最大应变和最小应变不相等。这种情况下,它们都是拉伸应变并且为循环载荷定义一个平均偏移
 m
m = (
 max
max +
 min
min) / 2。
如上所述,大多数基本疲劳数据都是使用完全反向载荷收集的。因此,这些数据不能直接用于具有非零平均值 (
 m
m
0) 的应变循环。为了针对使用拉伸或压缩平均应力的应变循环预测出更实际的寿命估计值,需要对使用完全反向载荷处理的试验结果进行校正。校正方法的选择取决于平均应力主要是拉伸还是压缩。
通过下图可发现其原因,该图示意性地说明了平均应力对应变寿命 (E-N) 曲线的作用。从概念上来看,拉伸平均应力的作用是打开裂缝,而压缩平均应力的作用是保持裂缝闭合。通常,这些作用集中体现在图中长应变寿命的末尾,拉伸平均应力缩短寿命,而压缩平均应力延长寿命。
由于计算某个范围平均应力的 E-N 曲线所需试验的费用太高,因此开发了几个经验关系曲线用于为平均应力的作用建模。在提出的所有方法中,有两种方法得到最广泛的认可:
• Smith-Watson-Topper 方法
• Morrow 修正
对于本质上主要是拉伸力的载荷序列,Smith-Watson-Topper 方法更加稳妥并且值得推荐。如果载荷主要是压缩力,尤其是对于完全压缩循环,Morrow 修正可用于提供更为实际的寿命估计值。
Creo Simulate 同时提供两种方法并且自动选取两者中最适合的方法。有关 Smith, Watson, Topper 方法的详细信息,请参阅
"A Stress-Strain Function for the Fatigue of Metals", Journal of Materials, Vol. 5, No. 4, 1970 (“针对金属疲劳的应力-应变功能”,《材料期刊》,第 5 卷,4 号,1970)。有关 Morrow 修正的详细信息,请参阅
"Fatigue Design Handbook", Advances in Engineering, Vol. 4, Society of Automotive Engineers, 1968 (“疲劳设计手册”,《工程展望》,第 4 卷,美国机动工程师协会,1968)。
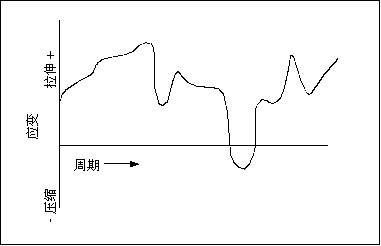
下一个图说明了更复杂的可变振幅载荷阵列,它接近于在实际结构中发现的循环应变。
对于可变振幅载荷,必须要从信号中提取疲劳损坏循环,然后评估每个循环完成的损坏。总损坏是每个单次循环导致的损坏的总和。由称为磁滞回线捕获的过程来提取每个疲劳循环。绘制的应力和应变的轨迹如下图所示。
当应力-应变磁滞回线闭合时,会返回应变范围和平均应力,并使用针对平均应力校正而修正的 E-N 曲线计算损坏。将在整个应变时间信号期间执行此分析,直到提取了所有循环并估算了总损坏为止。目前已开发出一个非常有效的算法用于执行循环提取,称为“雨流循环计数”(Rainflow Cycle Counting)。Creo Simulate 使用的就是此算法。
Creo Simulate 通常使用一个线弹性解来确定元件中的伪弹性应变。换句话说,该解忽略了塑性。在继续进行疲劳分析之前,会使用 Neuber 关系式将这些应变自动转换为非线性弹性-塑性应变。
影响疲劳寿命的因素
如上所述,E-N 曲线源自于基于沙漏形试样的应变控制试验。
一种标准化且完全反向的疲劳试验用于为一个约为 6 mm 直径的抛光试样确定基线 E-N 关系。在此试验中测量的疲劳极限或持久极限由

'
e 表示,但某个使用中的元件具有较低的极限
 e
e,这反映了对试验室外部试样的修正。特别是钢试样,有多个经验关系说明了由于以下因子
 e
e 的变化:
• 元件尺寸,Csize
• 载荷类型,Cload
• 凹槽的影响,Cnotch
• 表面粗糙度的影响,Csur < 1 (促进裂缝增长)
• 表面处理的影响,Csur >1 (抑制裂缝增长)
为说明这些影响,通常将特定修正因子应用于试验结果,以便:

e =
 'e
'eC
notchC
sizeC
loadC
sur......
其中,乘积的倒数 CnotchCsizeCloadCsur 统称为疲劳强度衰减因子 Kf:
Kf = 1 / (CnotchCsizeCloadCsur......)
需要切记的重要事项是,所有修正因子都是基于经验且谨慎使用的,通常仅适用于钢。除了大致的趋势外,通过它们几乎无法获得对疲劳过程本身的基本了解。尤其是,不应将它们用于超出它们测量的适用性以外的领域。
要了解有关影响疲劳寿命的因子的更多信息,请参阅以下部分:
元件尺寸的影响
金属中的疲劳源于在交变应力场的作用下裂缝式瑕疵的成核和随后的增长。其原理是疲劳失效起始于最弱的环节 (例如,定向最有利的金属晶体),然后通过定向不太有利的晶粒增长,直到发生最后的疲劳失效。从直观上看,似乎是受到交变应力作用的材料体积越大,越有可能更快地找到材料中最弱的环节。实际试验数据确实证实了材料尺寸的影响,尤其是在折弯和扭转条件下。
在折弯和较小程度的扭转试验中,通过截面建立的应力梯度在表面材料的薄层中集中了 95% 以上的最大表面应力。在大的截面中,此应力梯度的陡度要小于小截面。这样,可能包含关键瑕疵的可用材料体积会更大,从而导致疲劳强度衰减。对于不存在应力梯度的轴向拉伸,该影响是很小的。通过以下其中一个公式估算 Csize 的值。
如果试验试样轴的直径为 d < 6 mm:
Csize = 1
如果试验试样轴的直径为 6 mm < d < 250 mm
Csize = 1.189d-0.097
尺寸的影响对于旋转轴的分析尤为重要,例如,在车辆动力系中可能发现这一点。
对于元件不包含圆横截面情况,可使用以下等式计算具有宽度 (w) 和厚度 (t) 且受折弯作用的矩形截面的直径当量 deq:
deq2 = 0.65wt
载荷类型的影响
可以对使用某种循环载荷 (例如,轴向拉伸) 测量的疲劳数据进行“校正”,以表示那些在使用其它某种载荷方法 (例如扭转或折弯) 执行试验时应获得的数据。标准化的旋转折弯试验要求在完全反向折弯的条件下进行。
从一种载荷条件转移到另一种载荷条件时,要与持久极限
 e
e 一起使用的 C 载荷值详列如下:
测量的载荷 | | 目标载荷 | C load |
轴向 | 设置为 | 折弯 | 1.25 |
轴向 | 设置为 | 扭转 | 0.725 |
折弯 | 设置为 | 扭转 | 0.58 |
折弯 | 设置为 | 轴向 | 0.8 |
扭转 | 设置为 | 轴向 | 1.38 |
扭转 | 设置为 | 折弯 | 1.72 |
这样,使用此表中的值时,如果轴向拉伸载荷产生的应变为
 e
e,则在折弯载荷下产生的应变为 1.25
 e
e。
除了影响持久极限之外,载荷条件还会影响 Basquin 斜度 b,在以重对数标度绘制 E-N 曲线时使用该斜度。通常在 10
3 循环、

3

以及
e 处修正应变时,会将此影响考虑在内。以下因子用于定义 C'load,
 3
3修正因子:
测量的载荷 | | 目标载荷 | C' load |
轴向 | 设置为 | 扭转 | 0.82 |
折弯 | 设置为 | 扭转 | 0.82 |
扭转 | 设置为 | 轴向 | 1.22 |
扭转 | 设置为 | 折弯 | 1.22 |
表面粗糙度的影响
在所有疲劳失效中,有很大比例的疲劳失效会在元件的表面成核,以使表面条件成为影响疲劳强度的极重要的因素。通常,通过与抛光的试验室标准试样进行对比来判断各种表面条件。一般情况下,划痕、凹点、机械加工痕迹等等会提供附加的应力集中源来辅助裂缝成核的过程,从而影响疲劳强度。
下图说明了与较软钢相比,粗糙的表面粗糙度会对高强度钢产生更加不利的影响。因此,表面粗糙度校正因子 Csur < 1 与拉伸强度紧密相关。这里,表面粗糙度校正因子以定性术语将粗糙度分类,例如抛光、机械加工和锻造。
请注意,本图中所显示的某些曲线包含的影响仅仅不涉及表面粗糙度。例如,锻造曲线和热轧曲线包含脱碳的影响。
其它图通过使用曲面粗糙度的定量测量 (如 RA (均方根) 或 AA (算术平均)) 以更量化的方式来展现表面粗糙度校正因子。下图显示了曲面粗糙度对表面粗糙度校正因子的影响。
机械手册中提供了现成的与每个制造工艺关联的曲面粗糙度的值,如下例所示:
粗糙度类型 (微米) | 曲面粗糙度 |
车床成型加工 | 2.67 |
部分手工抛光 | 0.15 |
手工抛光 | 0.13 |
研磨 | 0.18 |
超精加工 | 0.18 |
研磨并抛光 | 0.05 |
表面处理的定性影响
如同表面粗糙度一样,表面处理也会大大地影响疲劳强度,尤其是持久极限。表面处理的净效应是改变自由曲面残余应力的状态。
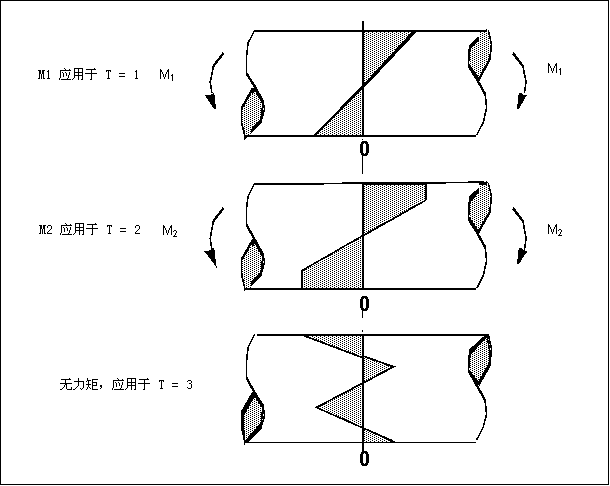
如果塑性变形未能在变形元件的整个横截面均匀分布,则会出现残余应力。在先前的图中,通过折弯使某金属条的表面因拉伸而变形。
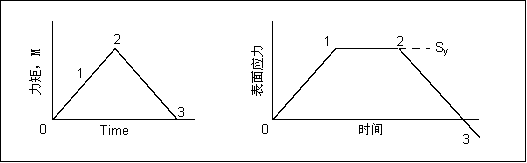
• 时间 T=1 时,施加了弯矩 M1,并且 M1 处于弹性范围内。
• 时间 T=2 时,弯矩增大为 M2 并且达到了屈服应力 (Sy),所以表面经受了塑性变形。
• 移除外力后,塑性变形区域会阻止邻近的弹性区域完成向无应变条件的弹性恢复。这样,弹性变形区域保留在残余拉伸的状态,而塑性变形区域处于残余压缩的状态。其结果是时间 T=3 时的应力分布。
在很多情况下,可以认为残余应力等同于通过外力产生的应力。这样,在元件表面存在的压缩残余应力会有效地减少疲劳失效的可能性。
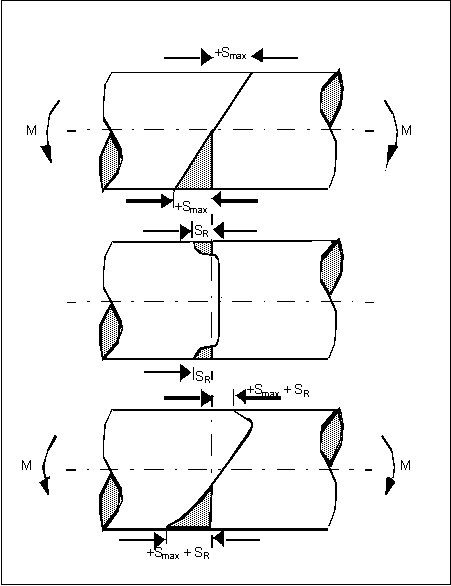
在上图中说明了施加的应力和残余应力的叠加作用。
• 顶部的示意图显示了在没有残余应力时,在弯矩 M 作用下某个梁中的弹性应力分布。
• 中间的示意图详示了与机械表面处理 (例如,喷丸强化) 关联的典型残余应力分布。请注意,材料表面的压缩应力被横截面内部等量的拉伸应力抵消。
• 在底部的示意图中,显示了由施加的应力 (由弯矩 M 引起) 与残余应力的代数和导致的应力分布。请注意,材料表面的最大拉伸应力已随残余应力的数量而减少。此外,拉伸应力的峰值位置现在已经移动到梁的内部。此应力的大小幅度取决于所施加应力的梯度和残余应力分布。在这些条件下,就有可能引发表面裂缝。
表面处理可大致分为机械工艺、热工艺和电镀工艺。头两种工艺提供了压缩层。电镀工艺提供了拉伸残余应力。以下详细说明了每种工艺:
• 机械处理 - 用于引入残余压缩应力的主要商用方法是冷轧和喷丸强化。尽管材料强度的某些改变是加工硬化的结果,但疲劳强度的改进主要是因为表面压缩应力的作用。表面滚压尤其适用于大零件,并且常常用于机轴和铁路轮轴的支承面等关键元件。使用滚压螺纹方法加工的螺栓的疲劳强度是使用传统方法加工螺纹的螺栓的两倍。
喷丸强化是使用合金钢粒或铸铁粒向元件表面喷射,这种处理方法尤其适于处理小批量生产的零件。
要切记的是,冷轧和喷丸强化对零件的长期寿命影响最大。它们对短期寿命的影响很小或没有影响。
对于其它修正因子,可以通过调整持久极限
 e
e 将校正因子用于说明这些通过机械方式引入的压缩应力的影响。通常,与喷丸强化关联的因子约为 1.5 至 2.0。
• 热处理 - 热处理是依赖于碳 (渗碳) 或氮 (渗氮) 在钢元件表面上或表面中的扩散的工艺。两种类型的原子都是空隙式的,也就是说它们占用邻近的铁原子之间的空间,因此增加了钢的强度并通过体积的变化导致在表面上留下了压缩残余应力。
渗碳通常分为三步进行处理:
◦ 将钢元件装在包含碳质固体的箱子中
◦ 密封箱子以便隔绝空气
◦ 加热到约为摄氏 900 度,加热的时间长短取决于需要的渗碳深度
也可以将元件放在炉子中加热并同时提供热的渗碳气体,如天然气。此种处理方法的优点是更快更精确。此外,在渗碳期之后可以紧接着进行扩散期处理,此时不必提供渗碳剂。这样可使某些碳原子进一步扩散到元件内部,从而减少梯度。
渗氮处理过程本质上与气体渗碳非常相似,除了使用氨气以及在较低的温度下对元件进行热处理之外。通常,在大约 550 摄氏度下处理 48 小时可得到约 0.5 mm 的渗氮层厚度。渗氮处理特别适合于处理精加工的有凹槽的元件,如齿轮和槽轴。下表举例说明了该过程的效果:
| 强度极限 (MPa) |
几何 | 未经渗氮处理 | 氮化处理 |
无凹槽 | 310 | 620 |
半圆凹槽 | 175 | 600 |
V 形凹槽 | 175 | 550 |
• 电镀 - 给钢元件镀铬和镍可在金属表面生成拉伸残余应力,从而将强度极限降低一半以上。这些拉伸应力是电镀过程本身的直接结果。在由机械形式产生的表面应力下,对于长寿命的元件以及使用较高强度的材料时,电镀的效果最明显。
在电镀过程之前引入压缩残余应力 (如喷丸处理或渗氮处理等) 可减少电镀的负面影响。另一种方法是在电镀后对元件进行退火,从而消除拉力。
表面处理对强度极限 (钢) 的定量影响
表面处理的效果取决于表面粗糙度。下表给出了由于表面处理而增加的强度极限应力:
| 强度极限的增加 |
精加工 | 喷丸处理 | 冷轧 | 氮化处理 |
抛光 | +15% | +50% | +100% |
研磨 | +20% | +0% | +100% |
去除材料 | +30% | +70% | +100% |
热轧 | +40% | +0% | +100% |
铸造 | +40% | +0% | +100% |
锻造 | +100% | +0% | +100% |
根据上表可知,无论表面粗糙度如何变化,应用表面处理均会产生后续影响。例如,如果加工将强度极限降低 30%,从上表可见,冷轧会将该极限提高 70% 来弥补损失。


 max) 和最小 (
max) 和最小 ( min) 应变大小相等但符号相反。通常将拉伸应变视为正,将压缩应变视为负。应变范围
min) 应变大小相等但符号相反。通常将拉伸应变视为正,将压缩应变视为负。应变范围  r 是在一次循环中最大应变和最小应变的代数差。
r 是在一次循环中最大应变和最小应变的代数差。 r =
r =  max–
max–  min
min a 是应变范围的一半。
a 是应变范围的一半。 a =
a =  r/2 = (
r/2 = ( max –
max –  max) / 2
max) / 2
 m = (
m = ( max +
max +  min) / 2。
min) / 2。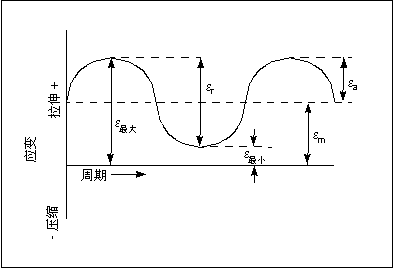
 m
m 0) 的应变循环。为了针对使用拉伸或压缩平均应力的应变循环预测出更实际的寿命估计值,需要对使用完全反向载荷处理的试验结果进行校正。校正方法的选择取决于平均应力主要是拉伸还是压缩。
0) 的应变循环。为了针对使用拉伸或压缩平均应力的应变循环预测出更实际的寿命估计值,需要对使用完全反向载荷处理的试验结果进行校正。校正方法的选择取决于平均应力主要是拉伸还是压缩。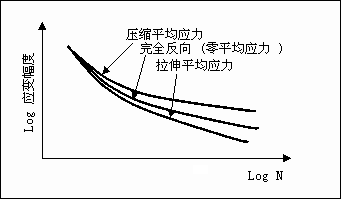

 'e 表示,但某个使用中的元件具有较低的极限
'e 表示,但某个使用中的元件具有较低的极限  e,这反映了对试验室外部试样的修正。特别是钢试样,有多个经验关系说明了由于以下因子
e,这反映了对试验室外部试样的修正。特别是钢试样,有多个经验关系说明了由于以下因子  e 的变化:
e 的变化: e =
e =  'eCnotchCsizeCloadCsur......
'eCnotchCsizeCloadCsur...... e 一起使用的 C 载荷值详列如下:
e 一起使用的 C 载荷值详列如下: e,则在折弯载荷下产生的应变为 1.25
e,则在折弯载荷下产生的应变为 1.25 e。
e。 3
3 以及 e 处修正应变时,会将此影响考虑在内。以下因子用于定义 C'load,
以及 e 处修正应变时,会将此影响考虑在内。以下因子用于定义 C'load, 3修正因子:
3修正因子: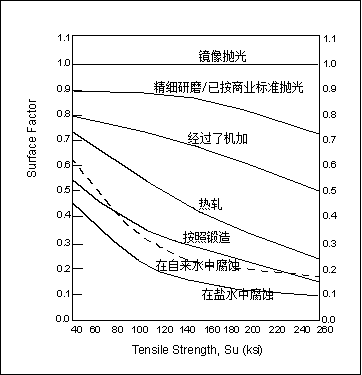

 e 将校正因子用于说明这些通过机械方式引入的压缩应力的影响。通常,与喷丸强化关联的因子约为 1.5 至 2.0。
e 将校正因子用于说明这些通过机械方式引入的压缩应力的影响。通常,与喷丸强化关联的因子约为 1.5 至 2.0。