包括突弹跳变
突弹跳变行为是结构位移中一种不稳定的行为。位移从一种配置跳变为另一种配置,甚至不会增大外部载荷。
急速恢复行为是结构位移中一种不稳定的行为,在此期间位移从一种配置跳变为另一种配置,甚至不会增大规定位移。
对于大多数非线性分析而言,牛顿型方法 (载荷控制方法) 用于在每一步中沿力-偏转曲线收敛到解。每个子步中载荷会按有限量增大,并且整个平衡迭代中载荷将保持固定。如果出现突弹跳变 (在载荷控制下),则一个极点可能存在两个解。载荷增大时,位移可能出现跳变,分析也可能因跳变大小而不收敛。同样,对于位移控制方法而言,载荷出现跳变时,也可能出现不收敛。
下图显示了非线性分析的载荷位移曲线,其中 λ 为所施加的载荷,μ 为位移。
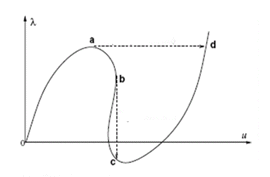
1. o-a-d:突弹跳变 (在载荷控制下)
2. o-a-b-c:突弹跳变 (在位移控制下)
在本示例中,采用的是载荷控制方法,分析在点 a 之后收敛失败,或会追踪路径 o-a-d,进而提供不完整或错误的结构稳定性信息。同样,对于位移控制方法而言,分析也可能在点 b 后收敛失败,并形成路径 o-a-b-c。
在载荷控制方法中,载荷步长保持恒定;在位移控制方法中,位移步长保持恒定。但在弧长法算法中,每次迭代时都用不同的因子代替载荷因子,以便解可以遵循指定的路径,直到实现收敛。该方法会记录平衡路径的附加载荷和位移对。
关于非线性分析中的弧长方法
对非线性平衡方程组的求解路径进行全面调查,将对研究结构的整体临界行为具有很大的现实意义。使用常规路径跟踪的方法被称为弧长方法。此类方法的基本思路是:为可确定未知载荷参数的非线性方程组添加约束条件。由于路径跟踪方法已日趋完善,因此文献上提供了多种不同方法。在众多现有的增量迭代非线性求解方法中,由 Riks 于 1979 年提出的弧长法 (后经 Crisfield 于 1981 年进行了修正) 是使用最广泛的方法。Creo Simulate 使用 Crisfield 弧长方法。
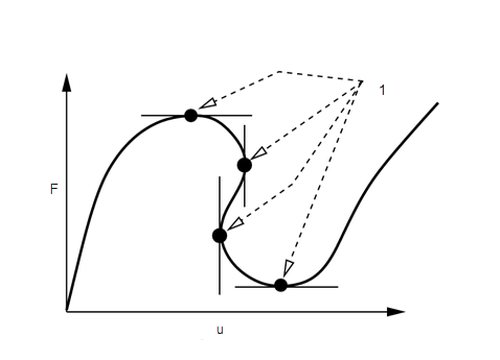
对于简单的结构,只需找出限制点 (在此限制点处,结构将不会再承受更多的载荷,且即将发生破坏) 处的载荷级别。破坏载荷通常会导致迭代求解过程无法收敛。对于其他模型,可能需要对结构的各个元件进行分析并获取有关响应性质、后限制点的信息 (参见图 1)。这样,当通过不稳定区域 (如图 2 所示) 时,便可了解整个结构的性能和稳定性,并将深入了解结构的行为。
图 1
1. 限制点
2. F - 载荷
3. u - 位移
图 2
1. 接下来是哪一个点?
2. F - 载荷
3. u - 位移
Crisfield 的球面弧长方法
Crisfield (1981) 在他的弧长方法中使用了超球面。在迭代过程中,同时使用了此方法与经过修正的 Newton-Raphson (m.N-R) 方法。在此方法中,每次迭代都不会重新生成和重新构建相切刚度矩阵,而是会保持固定不变,只有在每次增加载荷的开始阶段才会生成和构建相切刚度矩阵。图 4 定性说明了适用于求解一维问题的 Crisfield 方法和 m.N-R 方法。
图 4
1. 超球面
2. 平衡迭代
3. F - 外力
4. u - 位移
当从“收敛”(Convergence) 选项卡中选择“包括突弹跳变”(Include Snap-through) 时,将激活 Crisfield 的球面弧长方法,该方法可精确跟踪突弹跳变和急速恢复结构中的“载荷-位移”曲线。
对于大变形分析,如果为收敛方法选择“单通道自适应”(Single-Pass Adaptive) 或“快速检查”(Quick Check),则可选择“包括突弹跳变”(Include Snap-through) 来激活弧长算法。现在即可获取突弹跳变或后失稳问题的载荷位移历史记录。只能在必要的时候选择此选项,因为此选项会涉及附加的计算成本。
对于突弹跳变或后失稳分析,Creo Simulate 会在摘要 .rpt 文件中记录突弹跳变的起始位置和结束位置。
.ldc 文件是一个文本文件,其中包含以逗号分隔的值。.ldc 文件具有三列,用于为每个输出时间步长的三个量进行计算。
对于以下有限元方程组:
K.dx=df
X=X+dx
F=F+df
L2=SQRT(X.X)
SF=SQRT(dx.dx)/SQRT(X.X)
其中:
K - 切向刚度矩阵
dx - 给定载荷步长的变形矢量
df - 载荷增量
X - 总变形矢量
F - 总载荷矢量
LF - 载荷因子
L2 - 总变形的范数
SF - 跳变因子
对于 .ldc 文件:
◦ 第一列:LF - 载荷因子
◦ 第二列:L2=SQRT(X.X) - 模型中观察到的总变形的范数
◦ 第三列:跳变因子 SF=SQRT(dx.dx)/SQRT(X.X) - 较大的跳变因子表示突弹跳变分析失败的风险较大。
如果 .ldc 文件中第三列 (跳变因子 SF) 的值 > 0.95,则模型需要进行突弹跳变分析。在这种情况下,必须在“收敛”(Convergence) 选项卡上选择“包括突弹跳变”(Include Snap-through),然后运行分析。
通过查看
要在结果中查看突弹跳变中所述的位移测量与所施加载荷的图形,可以查看突弹跳变或失稳分析的载荷位移曲线。
选择最佳分析方法准则
• 如文献中所预期的那样,当结构在“载荷-挠度”路径的短长度上振荡时 (介于稳定平衡与不稳定平衡之间),弧长方法的表现最差。当弧长方法收敛至限制点时,您会开始注意到结构破坏错误。理论上,这类限制点处的结构刚度要么为零,要么为无限大,进而会导致数值失败。通常,当解收敛至限制点时,值得尝试不同的输出步长以确保您不会意外在限制点附近放置步长。布置输出步长时尽可能避免此类限制点,或将您的输出步长设置得较大些以避免出现限制点。对于短长度跳跃现象,默认的 m.N-R 方法经证实会比弧长方法更可靠。采用默认的 m.N-R 方法与合理的精细步长进行模拟,可以更深入地了解此类情况。
• 采用 m.N-R 方法与 Crisfield 弧长方法,有助于求解同时涉及水平和竖直相切限制点的问题。当结构在“载荷-挠度”路径的短长度上振荡时 (介于稳定平衡与不稳定平衡之间),采用弧长方法的数值体验是很令人满意的。在此类模型中,收敛速度以及算法所选的步长是非常有效的。
对方法的选择,需要具备一些工程方面的知识。如果这两种方法均无法收敛,您可能需要查看模型、载荷或求解策略。
书目
1. E. Ricks, An incremental approach to the solution of snapping and buckling problems. Int. J. Solids Structures 15,524-551 (1979).
2. Crisfield M.A. A fast incremental/iterative solution procedure that handles snap-through. Computer and Structures, 13(1):55–62, 1981