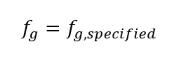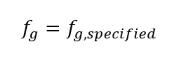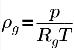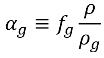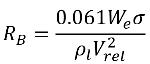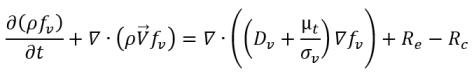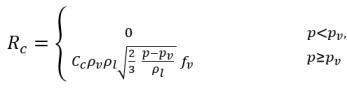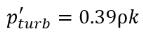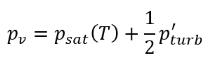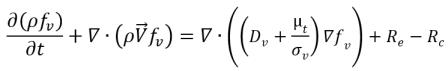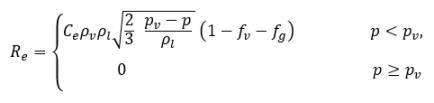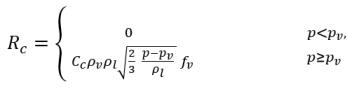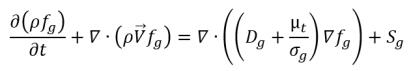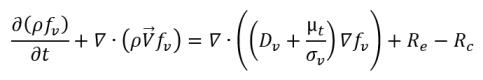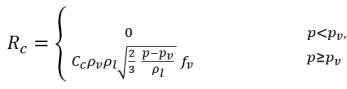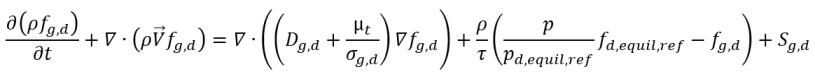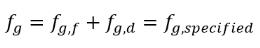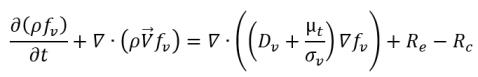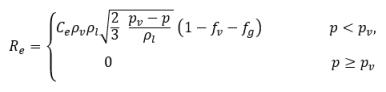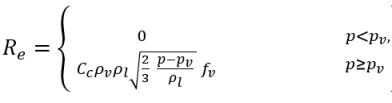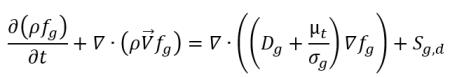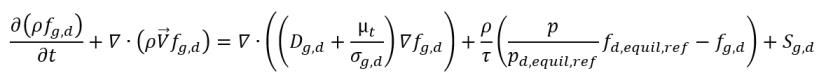空化模型

在 Creo Flow Analysis 中，与由 Singhal 等人提出的原始模型一样，空化流中的工作流体一直被认为是液体、蒸汽和一些不可凝结气体的混合物。默认情况下，空化模型会考虑液汽相变以及不可凝结气体的影响。基于不可凝结气体效应的建模方法，下表中提供了五种不同的模型，用于预测液相系统中的曝气和空化情况。本部分对这些模型进行了详细介绍。

NCG 模型	说明
恒定气体质量分数	由于 NCG (不可凝结气体) 质量分数是恒定的，因此这种气体被认为是具有微小可压缩气泡的不溶性气体
可变气体质量分数	与恒定气体质量分数模型类似，不过 NCG 质量分数是可变的，例如，入口可以引入不同的质量分数
平衡溶解气体模型	溶解在液体中的 NCG 的质量分数等于平衡值
溶解气体模型	溶解在液体中的 NCG 的质量分数取决于吸收或解吸速率以及平衡值
完整气体模型	结合了溶解气体模型和可变气体质量分数

恒定气体质量分数模型是 Creo Flow Analysis 中的基本或默认空化模型。该模型基于 Singhal 等人取得的工作成果。该模型假设在工作流体中，液体中始终存在的不可凝结气体 (NCG) 是遵循理想气体定律的非溶解性气体或自由气泡。尽管所有预设不可凝结气体都会随着空化区域压力的降低而自由膨胀，但是不可凝结气体的质量分数是预设的且在空化流中保持不变：

其中 fg,specified 是用户指定的值。

不可凝结气体的密度遵循理想气体定律：

其中 T 为流相温度，可以预设 (等温流量)，或者在考虑热传递时通过求解混合物能量守恒方程 2.168 来获得。根据方程 2.173，不可凝结气体的体积分数如下：

虽然 NCG 的质量分数固定不变，且通常具有非常小的值 (例如在天然水中，通常为 1.5e-05 或 15 ppm)，但其体积分数 αg 是可变的，且值可能会相当大。在空泡或低压区中，不可凝结气体与蒸汽争相填充空间中的空洞，这具体取决于气体和蒸汽密度。

对于液汽质量传递，会基于方程 2.194 和方程 2.195 构造蒸汽质量分数方程 2.169 中的空化源和汇项。具体而言，需要使用气泡生长和溃灭期间的已知流动物理量来估算气泡半径 RB。Singhal 等人认为，如果典型的气泡大小 RB 与极限 (最大可能) 气泡大小相同，则 RB 可以由气动阻力与表面张力之间的平衡确定。核工业中使用的关联式如下：

其中 Vrel 是液汽相对速度的模。在气泡流状态下 (即发生空化的情况下)，Vrel 通常较小，大约为液相速度的 5-10％。通过使用各种极限自变量，例如 RB→0 即表示 αv→0，以及基于每单位体积的相变速率应与供体相的体积分数 (或质量分数) 成正比这一事实，获得下列蒸汽产生/冷凝速率表达式以完成空化模型：

其中 Ce 和 Cc 是蒸发和冷凝系数，它们可以是用户指定的常量 (默认设置为 1.0) 或是已知流动物理量的函数。在方程 2.222 和方程 2.223 中，引入一个新的阈压 ρv 来替代方程 2.194 和方程 2.195 中的饱和蒸汽压 ρsat。根据 Singhal 等人提出的模型，为了解释湍流对空化流的影响 (通过实验研究观察)，将 Hinze 给出的湍流压力波动的局部值：

加到饱和蒸汽压上，以将相变阈压值升高到：

对于层流，pv=psat(T)

在考虑热传递且包括液体、蒸汽和不可凝结气体在内的所有相密度随温度变化时，饱和蒸汽压 psat 也是温度的函数。因此，此空化模型可以考虑对空化的直接热效应。

可变气体质量分数模型假定不可凝结气体始终保持为自由气体而无法溶解到液体中，但质量分数不再是预设的常数，这与恒定气体质量分数模型不同。相反，局部质量分数的分布由传输方程控制。而液汽质量传递通过方程 2.221、方程 2.222 和方程 2.223 中引用的同一空化模型进行建模。为清晰起见，下面给出了完整的建模方程组：

在空化流中，流体中的不可凝结气体将溶解到液体中或从液体中释放，以实现液相与气相间质量浓度的动态平衡。平衡溶解气体模型假设不可凝结气体的总质量分数保持恒定。但其中一部分可溶解到液体中以瞬时满足局部平衡条件。从数学分析的角度来看，除了相同的蒸汽质量分数方程和蒸汽质量传递模型之外，还求解了溶解气体质量分数 fgd (假设该方程始终处于平衡状态) 的附加传输方程。建模方程如下所示：

Sg,d	用户定义的气体溶解或释放定律
fd,equil,ref	在参考压力 pd,equil,ref 下溶解气体的平衡质量分数
fd,equil,ref 和 pd,equil,ref	用户指定的值

在此平衡模型中，时间尺度 Γ 逐渐趋近于 0，以使质量传递接近瞬时。请注意，在方程 2.231 中，自由气体的质量分数为 fg,f，而非 fg。自由气体的质量分数根据下列条件得到：

该模型放宽了液体中的溶解气体始终处于平衡状态这一条件。溶解气体的质量分数 (fg,d) 取决于组分的传输和溶解或释放速率 (有限速率)，而非瞬时质量传递的平衡条件。因此，溶解气体模型与平衡溶解气体模型共用相同的建模公式，方程 2.230 - 方程 2.234。但是，气体溶解和释放的有限质量传递速率使用不同的时间尺度 (Γ) 进行表征。对于液体中的气体吸收或气体溶解，Γ 由指定的吸收时间 (溶解气体的溶解时间默认为 10 秒) 给出。对于从液体中释放溶解气体，质量传递速率取决于指定的气体释放时间 (根据默认 Γ，溶解气体的释放时间为 10 秒)。

完整气体模型是溶解气体模型和可变气体模型的组合。不可凝结气体的质量分数会随时间和空间而变化，而与此同时，不可凝结气体也会发生气体溶解或吸收和释放。下面给出了完整的建模方程组：