MLE Method
The MLE (maximum likelihood estimation) method is considered to be the most robust parameter estimation method. It has very good statistical characteristics. The basic idea behind MLE is to obtain the most likely value of the parameters for a given distribution that best describes the data.
If x is a continuous random variable with probability density function, f(t;θ), where θ is the unknown parameter vector, then the likelihood function, in the case of complete data, is defined as:

The maximum likelihood estimators, θ, are the values of the parameter vector, θ, that maximizes L. The parameter vector (θ) that maximizes L also maximizes ln(L), and in most of the cases, it is easier to maximize the |ln(L) compared to L itself. The optimal values of θ that maximize ln(L) can be found as the simultaneous solution of the following equations:

Where m is the number of parameters.
In the case of a two-parameter Weibull analysis with complete data:

Therefore, the maximum likelihood estimators of θ and β (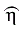 and
and 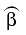 ) are:
) are:
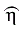 and
and 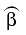 ) are:
) are:
Where β can be obtained by solving the following equation.
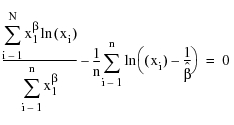
In some cases, MLE analyses are biased. To reduce the bias, modifications to the MLE method can be made. This is known as the MMLE (modified maximum likelihood estimation) method.