Chi-Square Fundamentals
The Chi-square (χ2) distribution is derived from the normal distribution. It is the distribution of a sum of squares of a number (ν) of independent standard normal variables (a mean of 0 and a variance of 1). If Z 1 , Z 2 , ..., Zv are mutually independent and identically distributed standard normal random variables, then, the following equation follows the χ2 distribution with ν degrees of freedom:

The probability density function (pdf), f(x), of the χ 2 distribution is: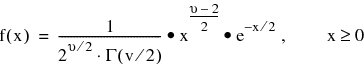
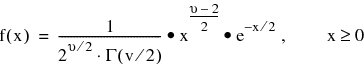
Here, ν is a positive integer, and Γ is the gamma function. If n is an integer, then Γ(ν) = (n -1)!. The mean and the variance of this distribution are ν and 2ν. It should be noted that the shape parameter ν is usually known as the degrees of freedom of the distribution. This distribution arises in many areas of statistics, including reliability applications. Particularly, it is used for assessing the goodness-of-fit of models and tests of significance (trend analysis and independency of variables for example), finding confidence intervals, and so on.
It should be noted that the χ 2 distribution is a special case of the gamma distribution with parameters α = ν / 2 and β = 1/2. The probability density function of the two-parameter gamma distribution is:

If α is an integer, then it is called the Erlangian distribution. The Erlangian distribution is the distribution of the sum of independent and identically distributed exponential random variables. It is used to find the reliability of standby systems.
We can find closed-form expressions for the cumulative distribution function (CDF) of the χ 2 distribution when the degrees of freedom (ν) is even. When ν = 2, then it reduces to the exponential distribution with rate parameter of 1/2 (for example, a mean of 2).