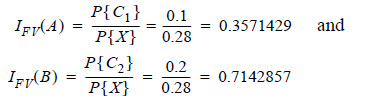The Fussell-Vesely importance measure is calculated quite differently than the Birnbaum or Criticality importance measures. It is constructed using minimal cut sets. A cut set is a set of basic events whose occurrence causes the top event to occur. A minimal cut set is a cut set that would not remain a cut set if any of its basic events were removed.

For example, the set of all the basic events is a cut set (or else the fault tree would be meaningless). If the fault tree consists of a single AND gate, then the cut set consisting of all the basic events is the only cut set and the minimal cut set. This is because all events leading into an AND gate must occur in order for the AND gate to be activated.

If the fault tree consists of a single OR gate, then the cut set consisting of all the basic events is not a minimal cut set unless there is only one basic event. This is because only one event leading into an OR gate needs to occur for the OR gate to be activated. In this case, any collection of basic events is a cut set. Therefore, given an OR gate, only those cut sets containing a single basic event are minimal cut sets.

Minimal cut sets are important in fault trees because they may be used to calculate the probabilities of events, including the top event. For example, the probability of the top event is given by the probability of the union of all the minimal cut sets.

Another interesting probability associated with the basic event A is the probability of the union of all minimal cut sets containing the basic event A. This is because the probability of the union of all minimal cut sets containing the basic event A is the probability that the top event is caused by a cut set containing the event A. This is a measure of the association of the basic event A with the top event X. It does not directly measure the probability that the top event X was caused by the basic event A, but it does indicate the potential importance of the basic event A.

A useful fact is that the probability of the union (OR) of sets is equal to the sum of the probabilities of the sets when the sets are mutually exclusive. If the sets are “nearly” mutually exclusive and, in addition, the basic events are independent and their probabilities are small, then this equality is approximately satisfied. For example, suppose that two minimal cut sets, C1 and C2, are given by C1 = {A and B and C} and C2 = {A and D}.

Then, exactly:

This idea is used in calculating the Fussell-Vesely importance measure. This measure considers the ratio of the probability of the union of all minimal cut sets containing the basic event A, divided by the probability of the union of all minimal cut sets. In practice, the numerator is replaced by the approximating sum of the probabilities of all minimal cut sets containing the basic event A, and the denominator uses the exact calculation, which is simply the probability of the top event X.

With the Fussell-Vesely importance measure, the fact that there is only one cut set for an AND gate leads to the uninformative result that all of the basic events leading to an AND gate will have the same value for the Fussell-Vesely importance measure.

Now, consider the previous example of the fault tree with an OR gate. Two minimal cut sets exist: C1={A} and C1={B}. Recall that P{A} = 0.1, P{B} = 0.2, and that P{X} = P{A or B} = 0.28. Note that C1 is the only minimal cut set containing the basic event A, and C2 is the only minimal cut set containing the basic event B. Also, P{C1} = P{A} = 0.1, and P{C2} = P{B} = 0.2. Therefore, the Fussell-Vesely importance measures for the basic events A and B are given by: