ODE 求解器
• 以下的每個函數皆會傳回 (intvls+1)×(n+1) 解題矩陣,其中 n 是未知數的數目。矩陣的第一欄含有 x 的值,會於此計算解。這些值是介於 x1 與 x2 之間,且等距為 (intvls + 1) 的數字。其餘的欄則含有求解值 y0、y1、...、yn-1,各對應於第一欄中的 x 值。
• 若是 rkfixed、RkAdapt、Bulstoer、Stiffb 及 Stiffr 等求解器,您可為解指定純量公差,方法是在呼叫求解器前,先行定義 TOL 變數。例如,您可將所有變數的公差設為 10-6:
TOL:=10-6
TOL 不會影響 Adams、BDF 或 Radau 求解器的公差。針對這些求解器,必須使用選用引數 tol 指定公差。
• 您可以使用 ODE 解題指令群,簡化方程式與初始條件的輸入。
非剛性系統求解器
• Adams(init, x1, x2, intvls, D, [tol]) - 使用 Adams 方法。
• rkfixed(init, x1, x2, intvls, D) - 使用第四階 Runge-Kutta 固定步距方法。
• Rkadapt(init, x1, x2, intvls, D) - 使用具備自適應步距大小的第四階 Runge-Kutta 方法。
• Bulstoer(init, x1, x2, intvls, D) - 使用 Bulirsch-Stoer 方法,此方法比 Runge-Kutta 更精確一些,但需要平滑變化的系統。
剛性系統求解器
下列函數可用來求解剛性或代數 ODE 問題。
• BDF(init, x1, x2, intvls, D, [J], [tol]) - 使用反向微分公式方法。您可以使用任一選用引數 J 或 tol 並省略另一個。
• Radau(init, x1, x2, intvls, D, [J], [M], [tol]) - 使用 Radau5 方法。您可使用選用引數 J、M 與 tol 的任意組合,並省略不想使用的選項。
• Stiffb(init, x1, x2, intvls, D, AJ) - 使用 Bulirsch-Stoer 方法。
• Stiffr(init, x1, x2, intvls, D, AJ) - 使用羅森布魯克方式。
混合求解器
• AdamsBDF(init, x1, x2, intvls, D, [J], [tol]) - 判斷系統為剛性或非剛性,並據以呼叫 Adams 或 BDF。您可以使用任一選用引數 J 或 tol 並省略另一個。
引數
• init 是 n 個實數初始值的向量 (其中 n 是未知數的數目),或單一純量初始值 (在單一 ODE 的情況下)。
• x1 與 x2 是求解 ODE 計算區間上的實數純量端點。init 中的初始值是在 x1 計算之 ODE 函數的值
• intvls 是用以內插解題函數的整數分隔區間數。解點數是區間數 + 1。
• D 是 D(x,y) 格式的向量函數,指定系統的右側。
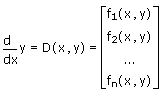
• tol (選用) 是實數或實數向量,指定系統中每個自變數的公差。公差是解答之變數的必要精確度。
◦ 您應將 tol 設為小於或等於 10-5。視問題規模與使用的相關步距大小之不同,可能需要降低 TOL 值,才可取得適當的解。tol 的值越小,求解器演算法需執行的步驟就越多,方能達到所需之精確度。
◦ 若要求解的是方程式系統,請將 tol 設定為純量,此純量指定的公差即等於系統中所有變數的公差。或將 tol 設定為向量,此向量指定每個變數的個別公差,且其長度等於系統中變數的數目。
• J (選用) 是 J(x, y) 形式的函數,會傳回雅可比矩陣:此矩陣含有 D 中相對於 y0、y1、... yn−1 之函數的偏導數。
• M (選用) 是實數矩陣,代表以 M · dy/dt = f(t, y) 形式表示的變數之間的任何偶合。
• AJ 是 AJ(x, y) 形式的函數,會傳回增廣雅可比,其第一欄含有系統右側函數的偏導數 (相對於 x)。其餘的欄是雅可比 J 的欄,含有相對於 y0、y1、... yn−1 的偏導數。
將 D、J 與 AJ 函數提供給求解器時,不提供其引數;而在 D、J 與 AJ 中指定函數 yn(x) 時,亦不會指定其引數。
D、J 與 AJ 的第二個引數必須下標為向量,即使只有單一項目亦然。
其他資訊
• 求解微分方程式時,函數 Radau 和 Rkadapt 會在內部使用非均等的步距大小,在解的較大變化區域中加入更多步距,但會傳回 intvls 所指定之等距點數的解。
• 使用 Radau 的好處在於不需要雅可比輸入,即使在已有 J 的情況下,使用 Radau 仍可提升精確度。