峰度和偏度值
• kurt(A, B, C, ...) - 傳回 A, B, C, ... 等元素的峰度。峰度的定義如下:
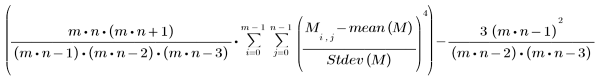
數值集的峰度表示與常態分佈相較下,分佈的平坦或起伏程度:
值 | 分佈形狀 |
|---|---|
kurt = 0 | 常態分佈 |
kurt > 0 | 相對起伏的分佈 |
kurt < 0 | 相對平坦的分佈 |
• skew(A, B, C, ...) - 傳回 A, B, C, ... 等元素的偏度值。偏度值的定義如下:
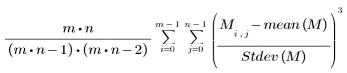
數值集的偏度值會量測均數的非對稱情形:
值 | 分佈形狀 |
|---|---|
skew = 0 | 分佈的均數呈對稱,常態分佈也不例外。 |
skew > 0 | 分佈「結尾」向正值延伸。 |
skew < 0 | 分佈「結尾」向負值延伸。 |
引數
• A, B, C, ... 是純量或陣列。kurt 的引數至少需要四個元素,skew 至少需要三個元素。
• M 是從函數引數 A, B, C, ... 建立的陣列。M 的標準差必須不等於零。