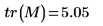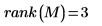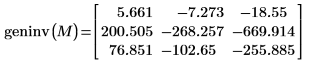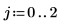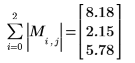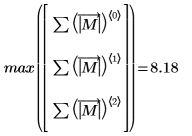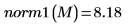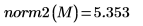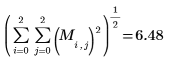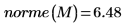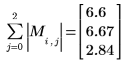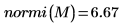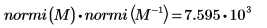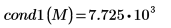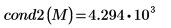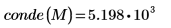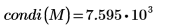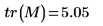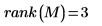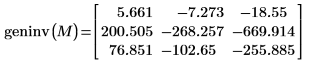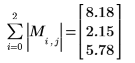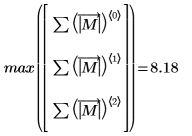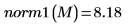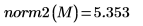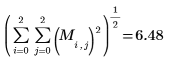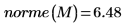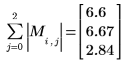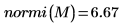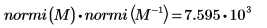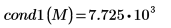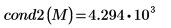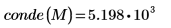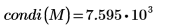範例：矩陣的特殊字元

向量、矩陣及表格 > 使用陣列 > 範例：矩陣的特殊字元

範例：矩陣的特殊字元

求解方形矩陣的繪線、順位、廣義逆轉、範數及條件數。

矩陣的繪線、順位及廣義逆轉

1. 使用 tr 函數求解 M 的繪線 (或對角元素總和)。

2. 使用 rank 函數求解實值矩陣 M 的順位。

3. 使用 geninv 函數求解矩陣 M 的廣義逆轉。

矩陣的不同範數

1. 求解 M 的 L1 範數，並與函數 norm1 的輸出結果進行比較

L1 範數是絕對欄數總和上限 (得自 j= 0, 1, 2 的 max)。

按一下以複製此運算式

<region id="ID0EZ3HHB" top="1056.0000000000002" left="19.200000000000003" height="136.00000000000003" width="191.66000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="53">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">max</id>
        <matrix rows="3" cols="1">
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>0</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>1</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
        </matrix>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
  </math>
</region>

2. 使用 norm2 函數求解 M 的 L2 範數。

3. 使用 norme 函數求解 M 的歐式範數：

矩陣的歐氏範數是向量的歐氏範數之類比：

<region id="ID0E2BIHB" top="1440.0000000000002" left="38.400000000000006" height="60.441333557128914" width="176.66000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="59">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <pow />
        <parens>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id xml:space="preserve">i</id>
              </boundVars>
              <apply>
                <summation />
                <lambda>
                  <boundVars>
                    <id xml:space="preserve">j</id>
                  </boundVars>
                  <apply>
                    <pow />
                    <parens>
                      <apply>
                        <indexer />
                        <id xml:space="preserve">M</id>
                        <sequence>
                          <id xml:space="preserve">i</id>
                          <id xml:space="preserve">j</id>
                        </sequence>
                      </apply>
                    </parens>
                    <real>2</real>
                  </apply>
                </lambda>
                <lowerBound>
                  <real>0</real>
                </lowerBound>
                <upperBound>
                  <real>2</real>
                </upperBound>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <real>2</real>
            </upperBound>
          </apply>
        </parens>
        <apply>
          <div />
          <real>1</real>
          <real>2</real>
        </apply>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
  </math>
</region>

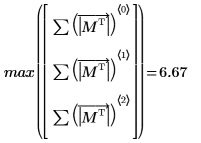
4. 求解 M 的無限範數，並與函數 normi 的輸出結果進行比較。

無限範數是絕對總列數上限 (得自 i=0, 1, 2 的 max)。

按一下以複製此運算式

<region id="ID0EBFIHB" top="1766.4000000000003" left="19.200000000000003" height="143.056" width="200.52000000000004" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="65">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">max</id>
        <matrix rows="3" cols="1">
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <apply>
                        <transpose />
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real>0</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <apply>
                        <transpose />
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real>1</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <apply>
                        <transpose />
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
        </matrix>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
  </math>
</region>

矩陣的不同條件數

矩陣的條件數是兩個矩陣範數的乘積，可測量線性系統解對輸入向量中之誤差的敏感度：

1. 使用 cond1 函數求解 M 的 L1 條件數。

2. 使用 cond2 函數求解 M 的 L2 條件數。

3. 使用 conde 函數求解 M 的歐式條件數。

4. 使用 condi 函數求解 M 的無限條件數。

相關主題

關於使用陣列

這是否有幫助?