範例:種子疊代與微分方程式
使用種子疊代預估解。
平方根
使用巴比倫法逼近數字的平方根。
1. 定義正實數 X 及其平方根的估值。
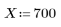
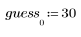
第一個估值會定義為向量的第一個元素。
2. 定義 N 作為疊代數。
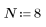
3. 計算平方根的新預估值。
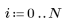
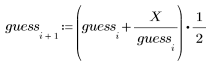
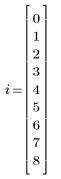 | 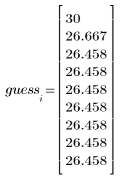 | 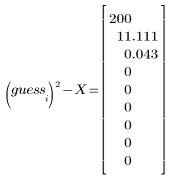 |
內建平方根函數提供下列結果:
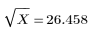
4. 繪製預估值的向量。
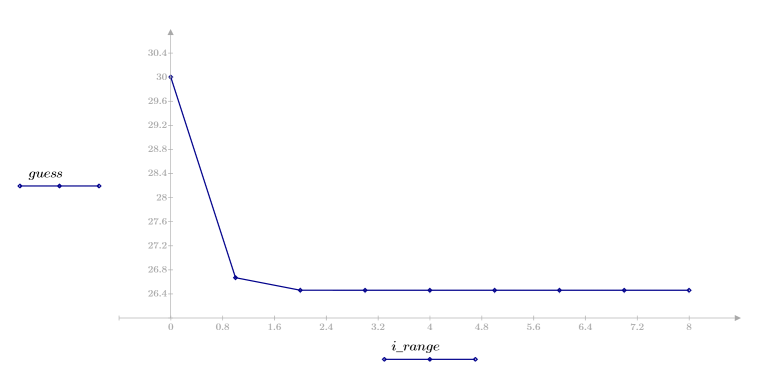
在此圖中,很快便出現收斂。而在其他情況下,您可以增加疊代數 N,以符合問題的需要。
微分方程式系統
請考量一個含有四個變數的感染模型:
• inf - 受感染個數
• sus - 易受感染個數
• dec - 死亡個數
• rec - 復原個數
1. 定義同步疊代的種子值。

2. 定義微分方程式系統。
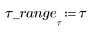
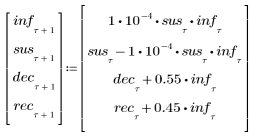
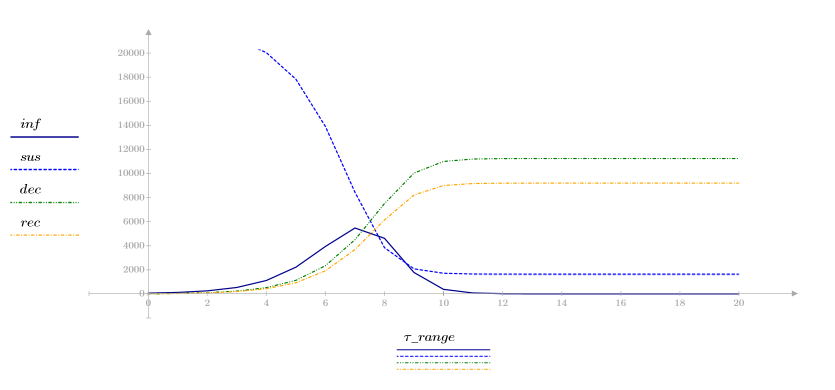
3. 依據時間繪製四個變數,以檢視感染模型的形成。
矩陣微分方程式
請考量馬可夫流程,也就是目前狀態由先前狀態乘以狀態移轉矩陣而求得的向量時間序列。
1. 定義初始向量狀態與狀態移轉矩陣 A。
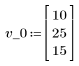

2. 定義疊代流程。
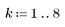
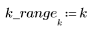
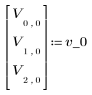
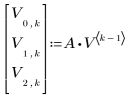
3. 計算向量的最終狀態。
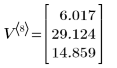
矩陣 V 包含流程的記錄:
