範例:逆轉換 idft
使用向量 (1D)
1. 定義向量 v 的長度。
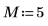
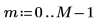
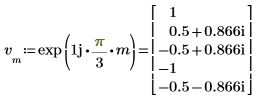
3. 使用 dft 函數計算向量 v 的正轉換。
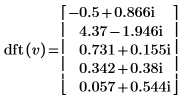
4. 使用 idft 函數計算向量 v 的逆轉換。

5. 顯示向量 v 的正轉換的逆轉換是原始向量 v。
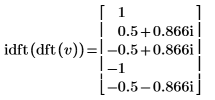 |  |
結果完全相同。
使用矩陣 (2D)
1. 定義與計算矩陣 C。
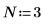
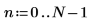
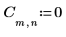
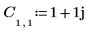
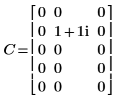
2. 使用 dft 函數計算矩陣 C 的正轉換。

3. 使用 idft 函數計算矩陣 C 的逆轉換。

4. 顯示矩陣 C 的正轉換的逆轉換是原始矩陣 C。
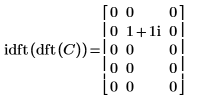 | 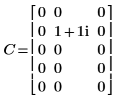 |
結果完全相同。
示範 idft 後面的基礎總和
一維情況:
1. 使用 exp 函數與總和運算子計算向量 v 的逆轉換。
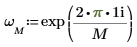
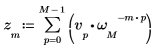
2. 比較所得出的向量 v 正轉換與 dft 函數的輸出。
 | 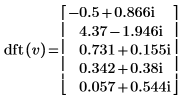 |
結果完全相同。
3. 使用總和運算子計算向量 v 的逆轉換。
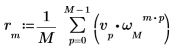
4. 比較所得出的向量 v 逆轉換與 idft 函數的輸出。
 |  |
結果完全相同。
二維情況:
1. 使用 exp 函數與總和運算子計算矩陣 C 的正轉換。
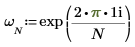
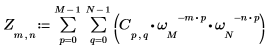
2. 比較所得出的矩陣 C 正轉換與 dft 函數的輸出。


結果完全相同。
3. 使用總和運算子函數計算矩陣 C 的逆轉換。
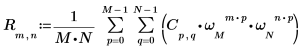
4. 比較所得出的矩陣 C 逆轉換與 idft 函數的輸出。


結果完全相同。