Нелинейная регрессия
• genfit(vx, vy, vg, F) — возвращает вектор, содержащий параметры, которые создают функцию F из параметров xn u1... un, наилучшим образом аппроксимирующую данные в vx и vy.
Функция genfit использует для минимизации оптимизированную версию метода Левенберга-Марквардта. Такая реализация зачастую бывает быстрее и менее чувствительна к начальным приближениям, но может не дать хорошей сходимости со многими локальными минимумами, такими как рациональные функции. Эта реализация чувствительна к неверным векторам производных.
Аргументы
• vx, vy — векторы вещественных значений данных одинаковой длины, соответствующие значениям x и y в наборе данных. Количество точек данных не должно быть меньше количества параметров.
• vg - это n-элементный вектор начальных приближений для параметров. Если n = 1, то vg - скаляр.
• F(x, u) - это аппроксимирующая функция или вектор функций, где x - независимая переменная, а u - либо вектор параметров, либо отдельные наименования параметров. Следующее уравнение является также допустимым представлением для аппроксимирующей функции:
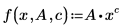
• n - положительное целое число. Если параметры не являются вектором, число индивидуальных наименований не может превышать девяти.
Улучшение сходимости
Чтобы улучшить сходимость и по возможности точность genfit, можно представить F как n+1-элементный вектор функций, в котором первый элемент F0 - это аппроксимирующая функция f, а остальные элементы F1, F2, …, Fn - это частные производные (в символьном виде) f по n параметрам.
В соответствии с двумя способами представления аппроксимирующей функции, приведенными выше, f(x,A,c) можно использовать только при нахождении частных производных аналитически. В представлении F в виде вектора функций число n не должно превышать 9, поэтому максимальная длина F равна 10. Можно создать вектор F, создав матрицу соответствующих частных производных и вычислив ее элементы аналитически:
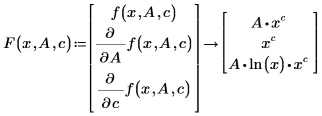
Дополнительная информация
• Для функции genfit необходимо ввести только имя аппроксимирующей функции или вектора функций без каких-либо аргументов.
• При использовании аппроксимирующей функции без символьных частных производных по параметрам функция genfit вычисляет частные производные по параметрам численно. Это менее точно, чем задание символьных производных, но может быть удобно в некоторых случаях.
• Если функция genfit не сходится, можно попытаться использовать другие начальные приближения или выполнить масштабирование данных таким образом, чтобы все параметры имели значения одного порядка. Как и все численные методы решения, нелинейные задачи очень чувствительны к начальным приближениям.
• Можно построить график аппроксимирующей функции с данными начальными приближениями, чтобы было легче уточнить их значения до использования genfit.
• Оптимизированный метод Левенберга-Марквардта более чувствителен к ошибкам в заданных алгебраических производных. Если выполнение функции genfit завершится неудачно, следует проверить выражения с производными.