Гамма-функции
• Функция Γ(z) — возвращает значение гамма-функции Эйлера от z.
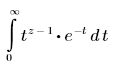
Могут быть полезными следующие уравнения, включающие гамма-функцию:
◦ Γ(z + 1) = z · Γ(z)
◦ Γ(z)·Γ(1 − z) = π · csc(π · z)
◦ Γ(n + 1) = n!
• Функция Γ(a, x) — возвращает значение неполной гамма-функции от x с параметром a. Γ(a, 0) = Γ(a).
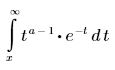
• Функция lnΓ(z) — возвращает значение натурального логарифма гамма-функции Эйлера, вычисленный в z.
Чтобы ввести Γ, нажмите клавиши G, Ctrl+G.
Используйте функцию lnΓ для возвращения малых результатов, затем масштабируйте их.
• Psi(y): возвращает производную натурального логарифма функции Γ(y).
Аргументы
• z - безразмерный вещественный или комплексный скаляр, значение которого не определено для z = 0, −1, −2...
Для функции Γ(z) только аргументы со значениями −107 ≤ Re(z) ≤ 171 и −106 ≤ Im(z) ≤ 106 могут быть вычислены без числового переполнения. Для комплексных параметров z, Γ(z) существует аналитическое продолжение вещественной функции.
• Параметр a — безразмерное, положительное вещественное скалярное значение.
• Параметр x — безразмерное, положительное вещественное скалярное значение или 0.
• y — вещественное число.