Пример. Использование оператора предела
Использование бесконечности в качестве ограничивающего значения
1. Используйте оператор предела и аналитически вычислите выражение при аргументе, стремящемся к бесконечности.
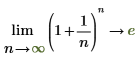
2. Постройте график функции для упрощения ее визуализации. Используйте горизонтальный маркер, чтобы представить e.
 |  |  |
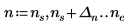 | ||
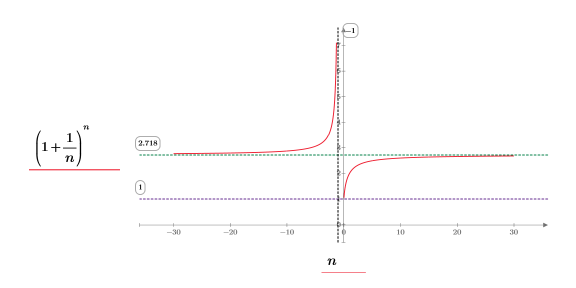 | ||
В квадранте (x, y) наблюдается следующее:
◦ По мере приближения n к positive infinity функция приближается к y=e.
◦ По мере приближения n к 0 функция приближается к y=1.
Математически это можно представить следующими аналитическими преобразованиями:
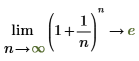 | 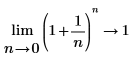 |
В квадранте (-x, y) наблюдается следующее:
◦ По мере приближения n к negative infinity функция приближается к y=e.
◦ По мере приближения n к -1 функция приближается к y=infinity.
Математически это можно представить следующими аналитическими преобразованиями:
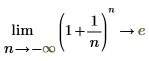 | 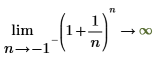 |
Использование во втором уравнении левостороннего предела означает, что приближение к -1 должно осуществляться с левой стороны кривой. Если это не указано, при расчете возвращается "не определено", так как функция не определена в интервале -1 < n < 0: 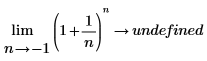 |
Использование стороны предела
1. Постройте график функции cot.
 | 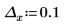 | 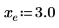 |
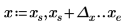 | ||
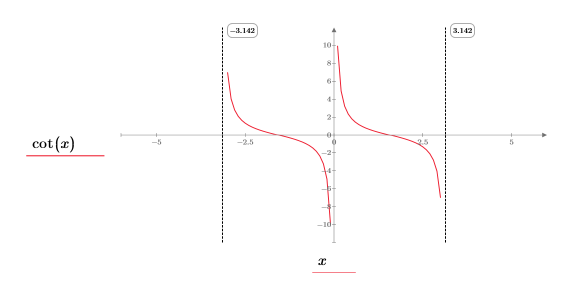 | ||
В квадранте (x, y) наблюдается следующее:
◦ По мере приближения x к 0 функция приближается к y=infinity.
◦ По мере приближения x к π функция приближается к y=-infinity.
Математически это можно представить следующими аналитическими преобразованиями:
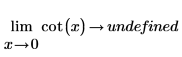 | 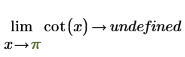 |
Поскольку функция симметрична относительно x=+/- n*π/2, аналитическое вычисление возвращает "неопределенность", так как функция в окрестностях x=0 (и любого числа, кратного π) может принимать значение infinity или -infinity, в зависимости от стороны, с которой x приближается к 0.
Это хороший пример для определения "стороны предела".
2. Определите "сторону предела" и повторно вычислите аналитически функцию cot в окрестностях точек 0 и π.
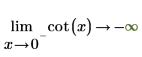 | 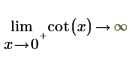 |
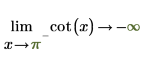 | 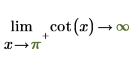 |
Возвращаемые результаты согласуются с графиком.
Иногда полезно построить график функции для ее визуализации и выполнить двойную проверку допустимости результатов аналитического вычисления. |