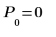Пример. Ознакомление с операцией определения и вычисления
Следует внимательно относиться к использованию операторов определения, вычисления и переменной-диапазона.
Если оператор переменной-диапазона используется для определения переменной, результат вычисления такой переменной зависит от способа вычисления:
• Если определение и вычисление выполняются последовательно, результат является вектором.
• Если определение и вычисление выполняются в отдельных областях, результат выглядит как вектор, но фактически является просто переменной-диапазоном.
Последовательное вычисление
1. Используйте оператор переменной-диапазона, чтобы последовательно определить и вычислить переменную n.
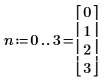
2. Убедитесь, что n является вектором, используя оператор элемента в матрице для извлечения его первого элемента.
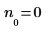
Непоследовательное вычисление
1. Используйте оператор переменной-диапазона, чтобы определить переменную p, а затем отдельно вычислить переменную p.
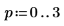
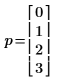
Результат выглядит как вектор, но фактически является переменной-диапазоном.
2. Убедитесь, что p не является вектором, использовав оператор элемента в матрице для извлечения первого элемента.
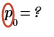
В сообщении об ошибке будет сказано следующее: это значение должно быть вектором.
3. Преобразуйте p в вектор P.
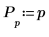
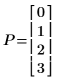
4. Убедитесь, что P является вектором, используя оператор элемента в матрице для извлечения его первого элемента.