Пример. Сигналы и классификация сигналов
Сигнал — это функция или набор данных, представляющие физическое количество или переменную. Обычно в сигнале содержится информация о поведении физического явления, например электрического тока, протекающего через резистор, звуковых волн сонара, распространяющихся под водой, или подземных толчков. Математически сигнал представляется в виде функции независимой переменной t, обычно обозначающей время. Таким образом, сигнал обозначается как x(t).
Непрерывные и дискретные сигналы
Сигнал x(t) является непрерывным, если t является непрерывной переменной. Если t является дискретной переменной, т. е. x(t) определяется в дискретные значения времени, тогда x(t) является дискретным сигналом, часто обозначаемым как x(n), где n — целое число. Дискретный сигнал x(n) может представлять явление, независимая переменная для которого по своей природе является дискретной, как ежедневная цена закрытия акции, или может быть получена путем выборки непрерывного сигнала x(t) при t = nT, где T представляет собой период выборки.
В следующих примерах главным образом рассматриваются дискретные сигналы. Ниже приведено несколько примеров часто встречающихся дискретных сигналов.
Единичный ступенчатый сигнал
1. Задайте единичную ступенчатую функцию с помощью ступенчатой функции Хевисайда.
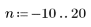
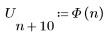
Ступенчатая функция Хевисайда устанавливает, что f(0)=0.5
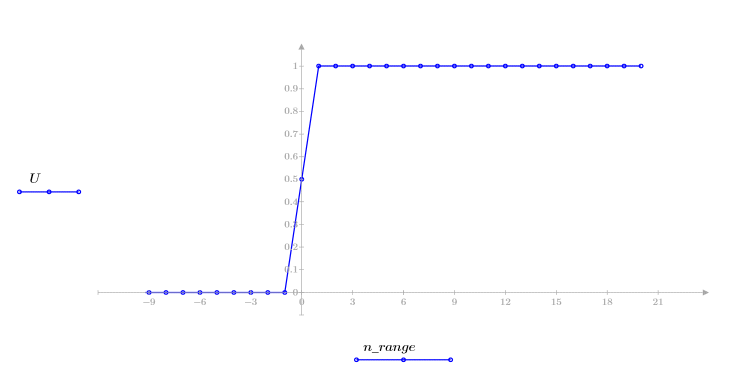
2. Определите область дискретных значений и постройте график единичной ступенчатой функции.
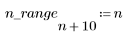
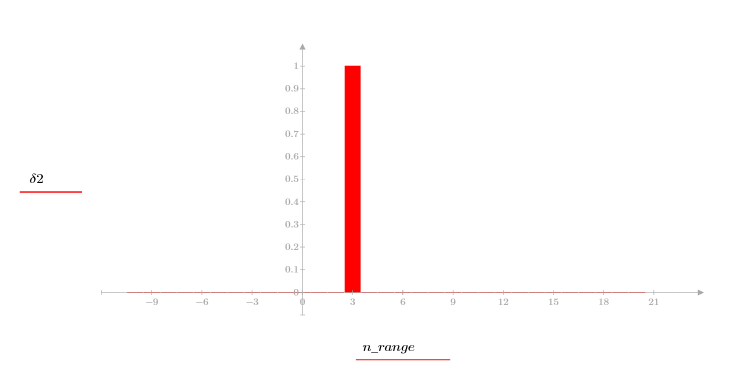
Единичный импульсный сигнал
1. Задайте единичную импульсную функцию.
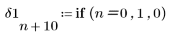
2. Постройте график единичной импульсной функции.

3. Задайте значение k для сдвига импульса на k выборок вправо.
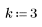
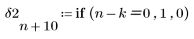
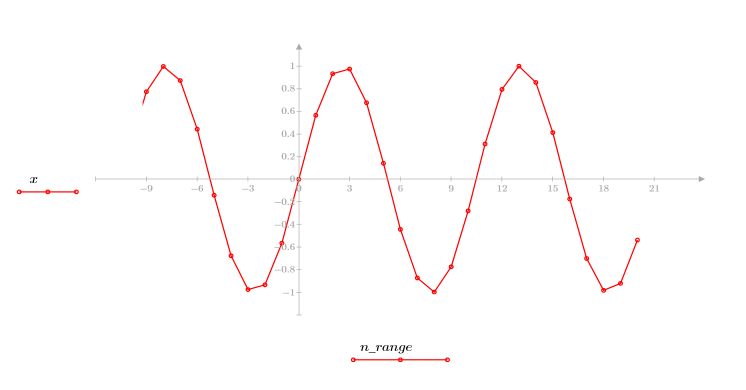
Синусоидальный сигнал
1. Задайте частоту.
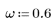
2. Задайте синусоидальную функцию.
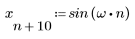
3. Постройте график полученной функции.
Экспоненциальный сигнал
1. Задайте коэффициент альфа.
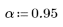
2. Задайте экспоненциальную функцию.
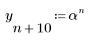
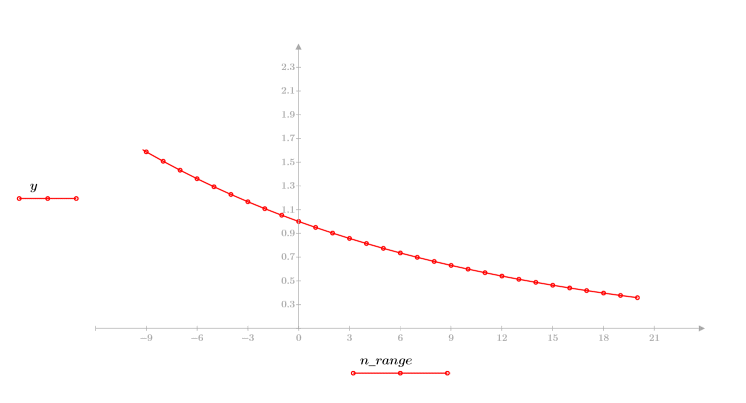
3. Постройте график экспоненциальной функции.
Экспоненциально затухающая синусоида
Постройте график функции, получившейся в результате произведения синусоидальной функции на экспоненциальную.
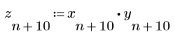
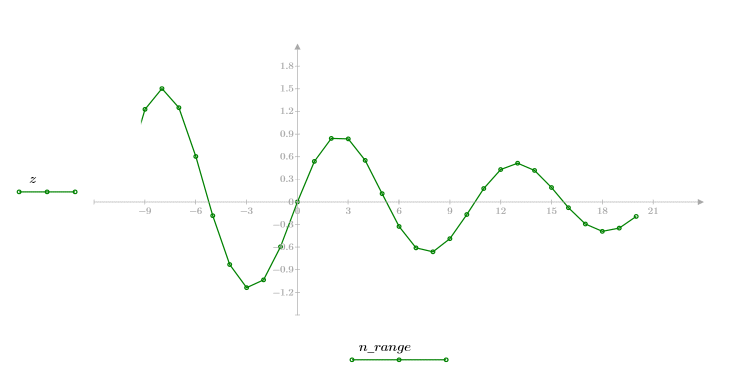
В результате получается экспоненциально затухающая синусоидальная функция.
Аналоговые и цифровые сигналы
Если непрерывный сигнал x(t) может принимать любое значение в течение непрерывного интервала времени, тогда x(t) называется аналоговым сигналом. Если дискретный сигнал x(n) может принимать только конечное количество различных значений, он называется цифровым сигналом. Аналоговый сигнал для преобразования в цифровой необходимо дискретизировать и квантовать.
Вещественные и комплексные сигналы
Сигнал x(t) является вещественным сигналом, если его значения выражаются вещественными числами. Подобным образом, сигнал x(t) является комплексным сигналом, если его значения выражаются комплексными числами. Используйте функции phase и phasecor для управления комплексными сигналами.
Детерминированные и случайные сигналы
Детерминированные сигналы — это такие сигналы, значения которых полностью определены для любого заданного времени. Таким образом, детерминированный сигнал можно моделировать с помощью известной функции времени x(t). Напротив, случайные сигналы — это такие сигналы, которые могут принимать случайные значения в любое заданное время. Случайные сигналы можно характеризовать только статистически. Функции генерирования шумов whiten, gaussn и onefn производят псевдослучайные сигналы, характеризующиеся пользовательскими статистическими параметрами.