Пример. Кадрирование сигнала
Для кадрирования сигнала используются следующие функции:
Импульсная характеристика с идеальными/обрезанными нижними частотами
1. Задайте импульсную характеристику h идеального фильтра нижних частот с нормализованной частотой среза 0,15.
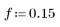
2. Задайте импульсную характеристику.
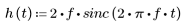
Поскольку реализуемый фильтр с конечной длительностью должен обладать импульсной характеристикой конечной длительности, идеальная характеристика обрезается до некоторого управляемого количества элементов.
3. Для проверки эффекта прямой обрезки без кадрирования по частотной характеристике задайте фильтр длины N, состоящий просто из центральных N элементов идеальной характеристики, сдвинутых так, чтобы сделать фильтр причинным.
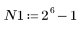
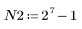
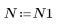
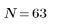
В качестве упражнения задайте N как N2 и пронаблюдайте на нижеприведенных примерах эффект увеличения количества элементов.
4. Примените функцию импульсной характеристики по всему диапазону элементов и постройте график результирующей функции.
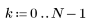
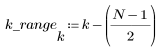
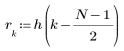
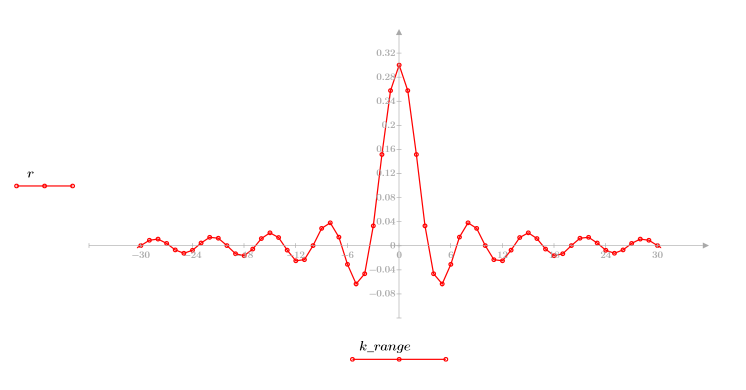
5. Рассчитайте частотную характеристику данного обрезанного сигнала с помощью функции gain, но вначале задайте диапазон частот (кратный частоте выборки).
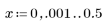
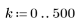
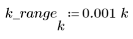
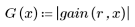
6. Соберите дискретные величины функции gain в новый массив.
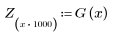
7. Найдите максимальную величину G и соответствующую ей частоту.
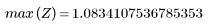
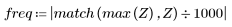
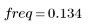
Если количество элементов равно N1=63, максимальный коэффициент передачи 1.083 наблюдается на частоте freq=0.134.
Если количество элементов равно N2=127, максимальный коэффициент передачи 1.092 наблюдается на частоте freq=0.142, перемещаясь ближе к краю полосы.
На частоте freq=0.2 коэффициент передачи падает практически до нуля. Сравните коэффициент передачи в области данной частоты в каждом из следующих примеров.
8. Постройте график функции gain в заданном диапазоне и покажите частоту, на которой величина принимает максимальное значение.
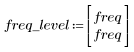
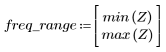
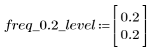
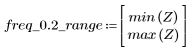
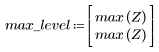
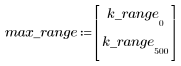
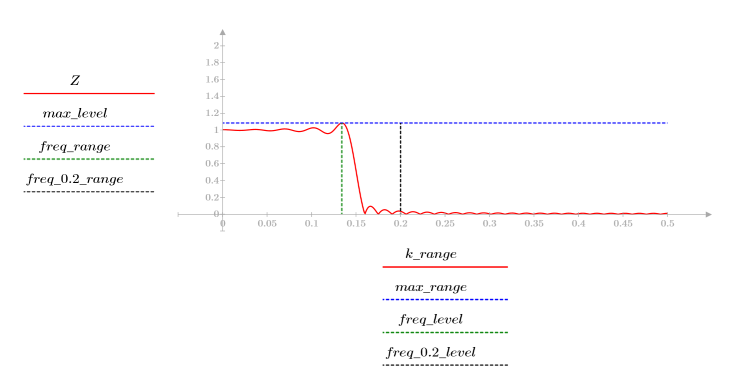
Отклонение на краю полосы пропускания известно как явление Гиббса. Вышеописанное увеличение порядка фильтра N с N1=63 до N2=127 приближает отклонение к краю полосы, но не уменьшает его амплитуды.
Переход от 1 к 0 с увеличенными значениями порядка фильтра N становится более резким.
Одним из способов создания более желаемой частотной характеристики является кадрирование идеальной импульсной характеристики так, чтобы переход к 0 на краях импульсной характеристики фильтра стал более гладким. Кадры, элемент за элементом, перемножаются на вектор отклика r.
Треугольное окно
Функция triangular возвращает треугольное окно или окно Бартлетта ширины N.
j-ый элемент результирующего вектора имеет вид:
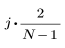
для
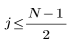
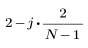
для
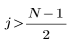
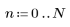
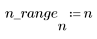
1. Примените функцию к последовательности фильтрации N и постройте график результирующего вектора.
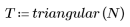
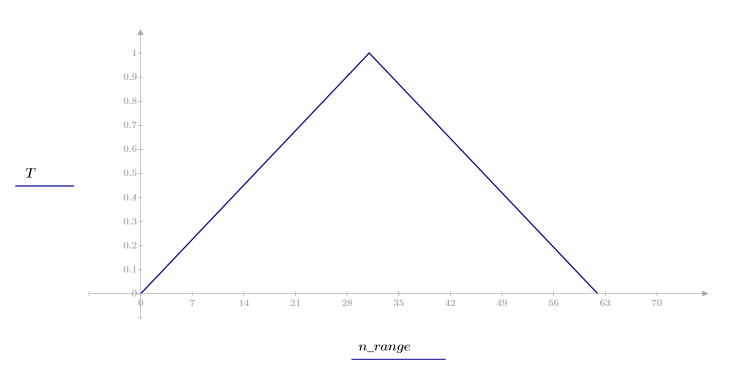
2. Рассчитайте отклик кадрированного импульса.
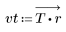
3. Функция gain используется для расчета и построения графика коэффициента передачи в дБ данного фильтра с коэффициентами vt на частоте k/1000.
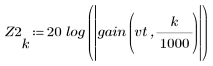
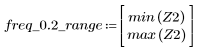
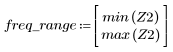
Окно Хенинга
Функция hanning возвращает окно Хенинга ширины N.
k-ый элемент результирующего вектора имеет вид:
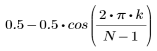
1. Примените функцию к последовательности фильтрации N и постройте график результирующего вектора.
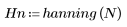
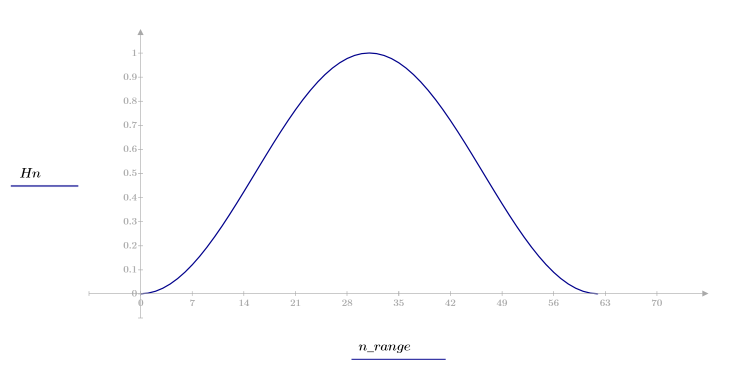
2. Рассчитайте отклик кадрированного импульса.
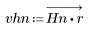
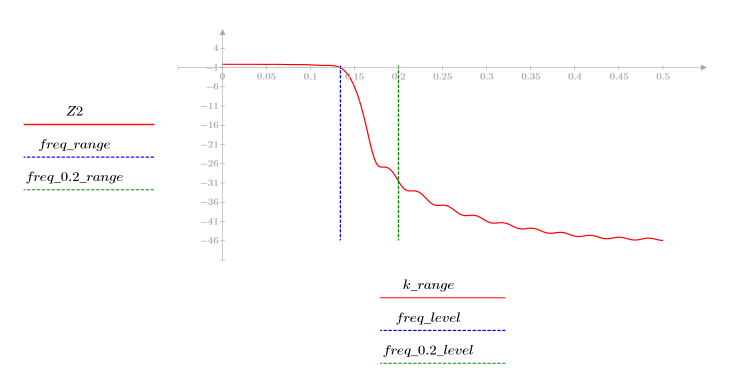
3. Функция gain используется для расчета и построения графика коэффициента передачи в дБ данного фильтра с коэффициентами vhn на частоте k/1000.
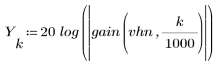
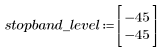
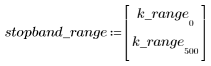
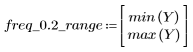
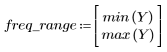
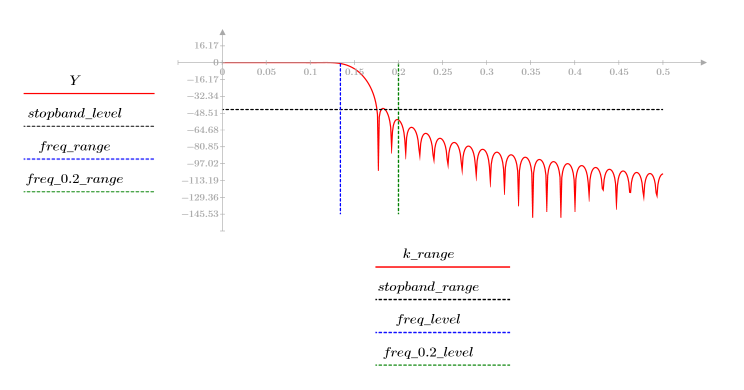
Пульсация полосы затухания около -45 дБ.
Окно Хэмминга
Функция hamming возвращает окно Хэмминга ширины N.
k-ый элемент результирующего вектора имеет вид:
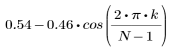
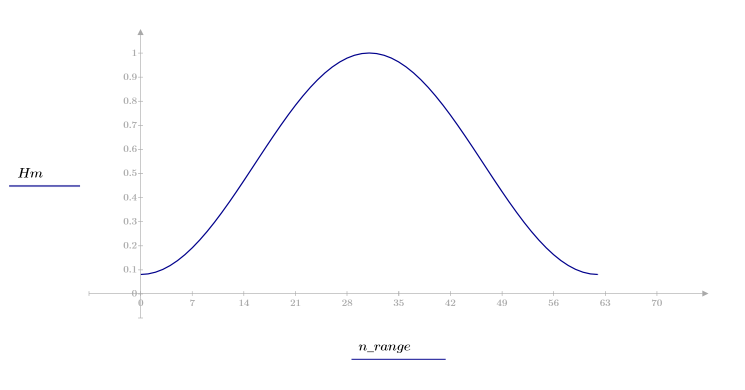
1. Примените функцию к последовательности фильтрации N и постройте график результирующего вектора.
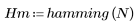
2. Рассчитайте отклик кадрированного импульса.
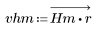
3. Функция gain используется для расчета и построения графика коэффициента передачи в дБ данного фильтра с коэффициентами vhm на частоте k/1000.
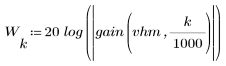
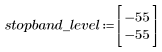
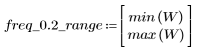
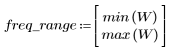
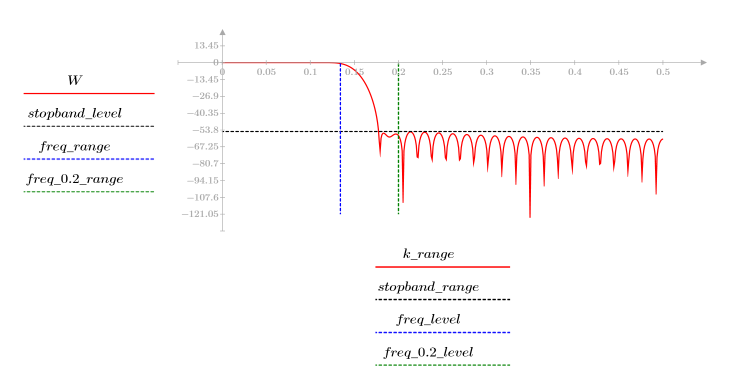
Пульсация полосы затухания около -55 дБ.
Окно Блэкмена
Функция blackman возвращает окно Блэкмена ширины N.
k-ый элемент результирующего вектора имеет вид:
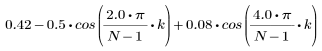
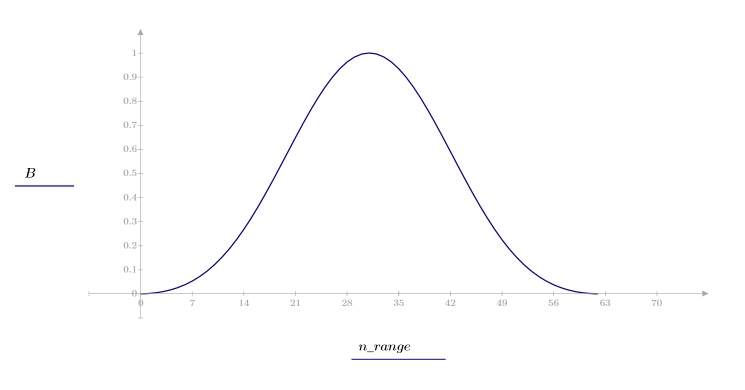
1. Примените функцию к последовательности фильтрации N и постройте график результирующего вектора.
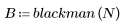
2. Рассчитайте отклик кадрированного импульса.
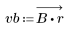
3. Функция gain используется для расчета и построения графика коэффициента передачи в дБ данного фильтра с коэффициентами vb на частоте k/1000.
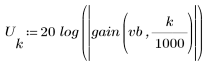
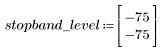
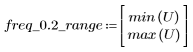
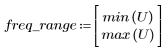
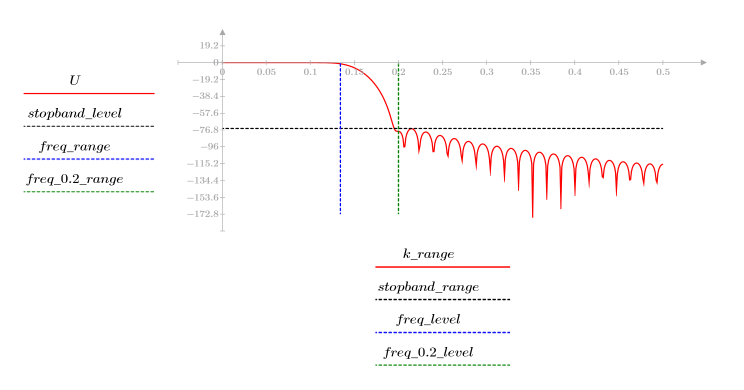
Пульсация полосы затухания около -75 дБ.
Окно Нуттела
Функция nuttall возвращает окно Нуттела ширины N.
k-ый элемент результирующего вектора имеет вид:
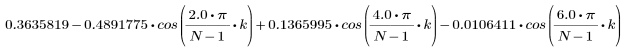
1. Примените функцию к последовательности фильтрации N и постройте график результирующего вектора.
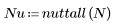
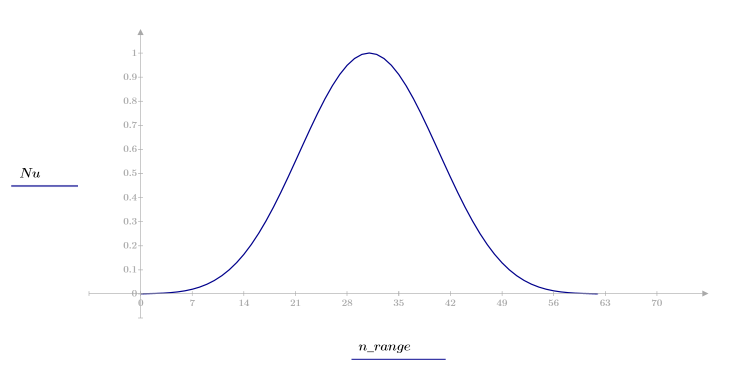
2. Рассчитайте отклик кадрированного импульса.
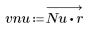
3. Функция gain используется для расчета и построения графика коэффициента передачи в дБ данного фильтра с коэффициентами vnu на частоте k/1000.
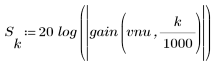
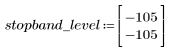
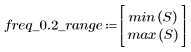
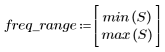
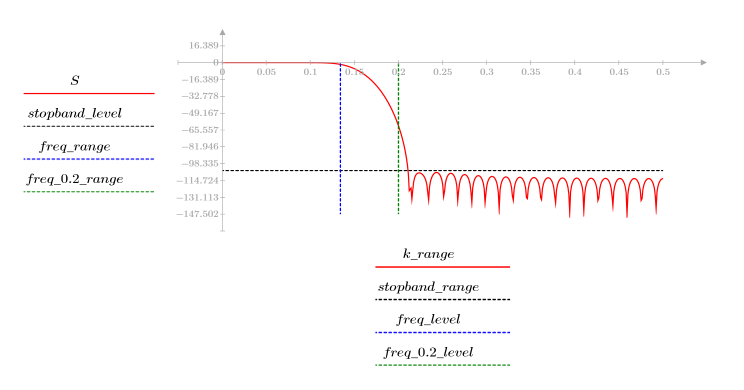
Пульсация полосы затухания около -105 дБ.
Трапециевидное окно
Функция taprect возвращает трапециевидное окно ширины N.
Это окно горизонтальное в середине на высоте 1 с конусовидными концами, образуемыми косинусоидами. С правой и левой стороны используются значения:
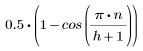
где
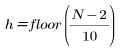
и n изменяется от 0 до h.
1. Примените функцию к последовательности фильтрации N и постройте график результирующего вектора.
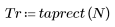
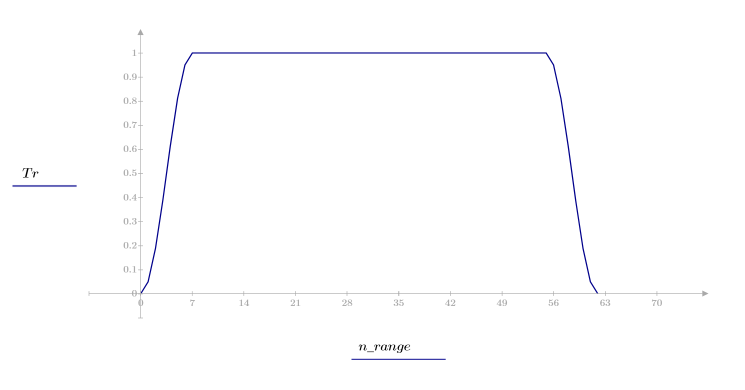
2. Рассчитайте отклик кадрированного импульса.
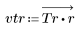
3. Функция gain используется для расчета и построения графика коэффициента передачи в дБ данного фильтра с коэффициентами vtr на частоте k/1000.
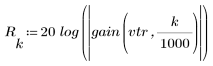
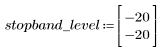
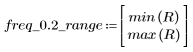
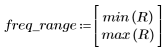
Окно Гаусса
Функция gaussian возвращает окно Гаусса ширины N и с параметром a. Число a является вещественным числом, пропорциональным обратной гауссовой дисперсии и удовлетворяющим условию 2 < a < 20.
k-ый элемент результирующего вектора имеет вид:
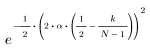
1. Примените функцию к последовательности фильтрации N и постройте график результирующего вектора.
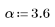
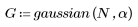
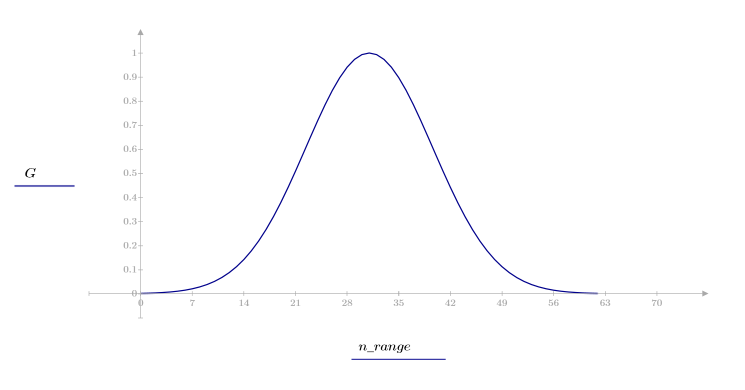
2. Рассчитайте отклик кадрированного импульса.
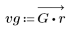
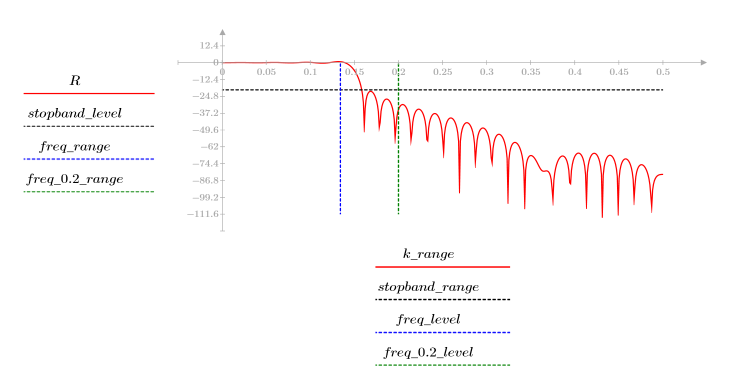
3. Функция gain используется для расчета и построения графика коэффициента передачи в дБ данного фильтра с коэффициентами vg на частоте k/1000.
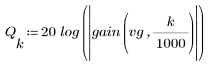
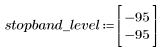
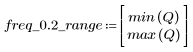
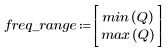
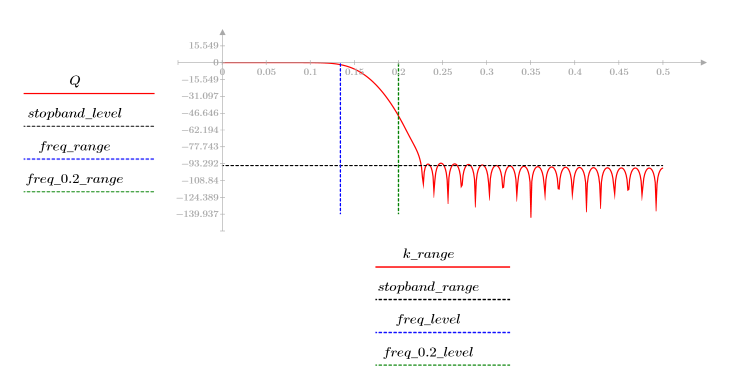
Пульсация полосы затухания около -95 дБ.
Окно Кайзера
Функция kaiser возвращает окно Кайзера ширины N и с параметром b. Параметр b должен удовлетворять условию 2≤b≤20.
k-ый элемент результирующего вектора имеет вид:
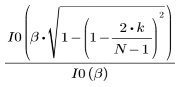
1. Примените функцию к последовательности фильтрации N и постройте график результирующего вектора.
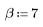
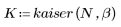
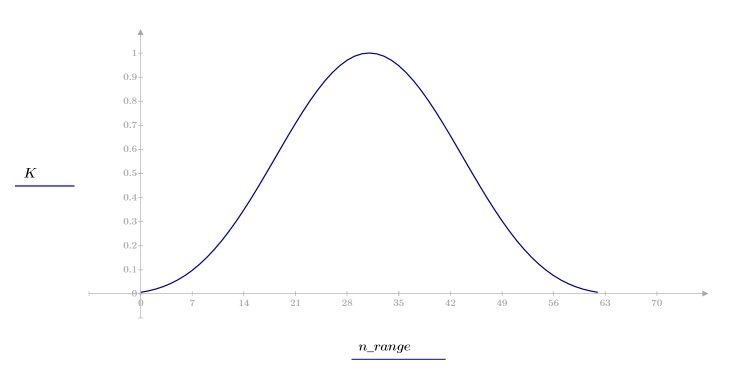
2. Рассчитайте отклик кадрированного импульса.
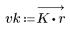
3. Функция gain используется для расчета и построения графика коэффициента передачи в дБ данного фильтра с коэффициентами vk на частоте k/1000.
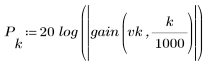
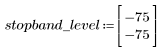
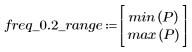
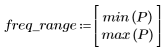
Пульсация полосы затухания около -75 дБ.
Окно Чебышева
Функция cheby возвращает окно Чебышева, или окно с равномерными пульсациями, ширины N и с параметром b. Параметр b определяет максимальную пульсацию боковых лепестков в дБ и должен удовлетворять условию 1 < b; обычно b > 50. Длина данного окна должна быть нечетной. Окно Чебышева рассчитывается посредством обратного дискретного преобразования Фурье полинома Чебышева, оцененного в точках, расположенных вокруг единичной окружности. Дополнительные сведения о данном окне см. в издании "Programs for Digital Signal Processing" (IEEE Press) (Программы цифровой обработки сигналов; изд-во IEEE Press) (на английском языке).
1. Примените функцию к последовательности фильтрации N и постройте график результирующего вектора.
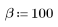
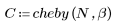
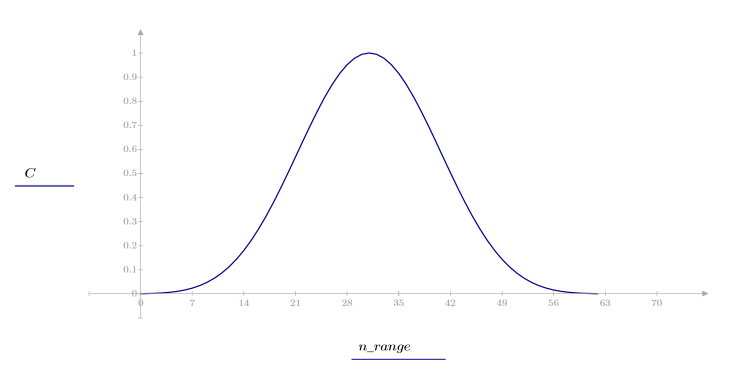
2. Рассчитайте отклик кадрированного импульса.
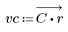
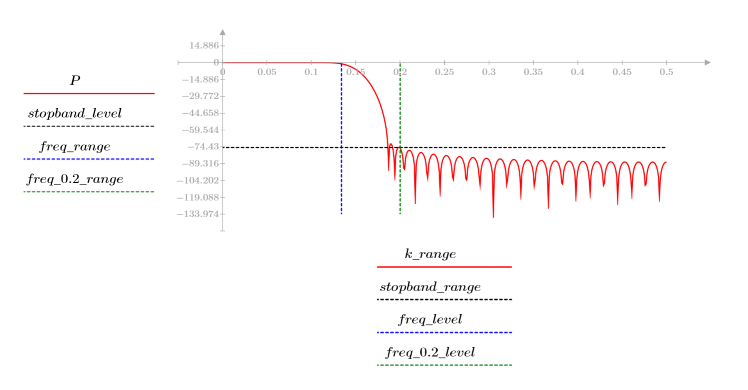
3. Функция gain используется для расчета и построения графика коэффициента передачи в дБ данного фильтра с коэффициентами vc на частоте k/1000.
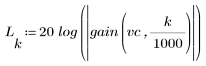
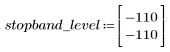
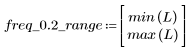
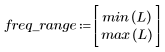
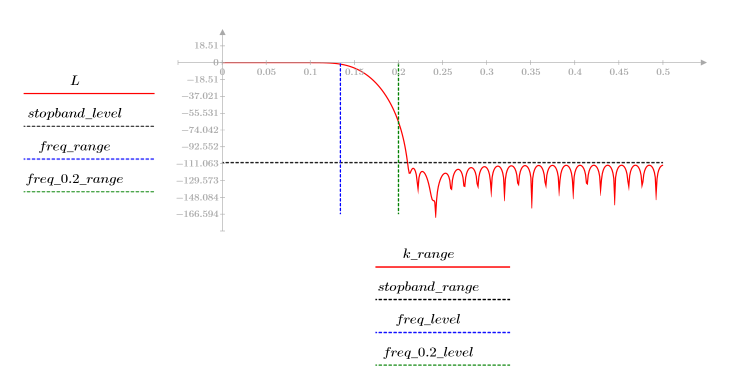
Пульсация полосы затухания около -110 дБ.
Косинусное окно
Функция costaper подобна функции taprect в том смысле, что она возвращает прямоугольное окно с конусовидными концами, совпадающими по форме с косинусоидой. Однако параметр a можно использовать для определения процентной части окна, которая должна быть создана с помощью косинусоиды. Значение параметра a должно лежать между 0 и 1; значение, равное 0, возвращает прямоугольное окно, в то время как значение, равное 1, возвращает возрастающую косинусоиду.
Значение k-го элемента для конусовидной части окна имеет вид:
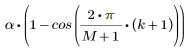
где M — количество элементов окна, находящихся в одном из хвостов, имеет вид a-N:
1. Примените функцию к последовательности фильтрации N и постройте график результирующего вектора.
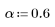
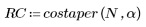
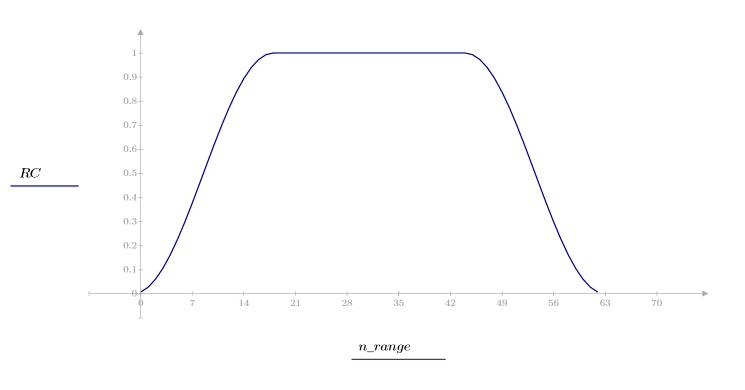
2. Рассчитайте отклик кадрированного импульса.
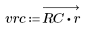
3. Функция gain используется для расчета и построения графика коэффициента передачи в дБ данного фильтра с коэффициентами vrc на частоте k/1000.
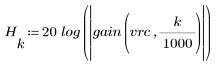
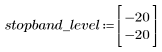
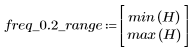
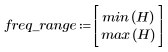
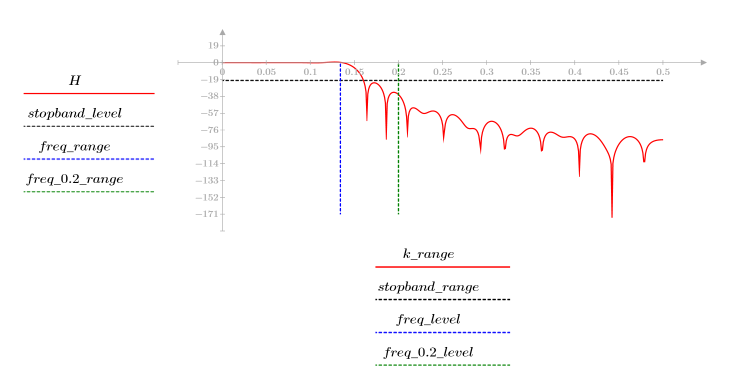
Пульсация полосы затухания около -20 дБ.
Справочная информация
• S. Lawrence Marple, Jr., Digital Spectral Analysis with Applications (Цифровой спектральный анализ с приложениями), Prentice-Hall, 1987.
• Lawrence R. Rabiner and Bernard Gold, Theory and Application of Digital Signal Processing (Цифровая обработка сигналов. Теория и применение), Prentice-Hall, Inc., 1975.
• T. W. Parks and C. S. Burrus, Digital Filter Design (Проектирование цифровых фильтров), Wiley-Interscience, 1987.