Пример. Итерация начальных чисел и разностные уравнения
Оцените решения, используя итерацию начальных чисел.
Квадратные корни
Для аппроксимации квадратного корня числа используется вавилонский метод.
1. Задайте положительное вещественное число X и начальное приближение его квадратного корня.
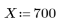
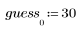
Первое приближение определяется как первый элемент вектора.
2. Задайте N в качестве числа итераций.
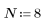
3. Рассчитайте новые оценки значения квадратного корня.
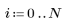
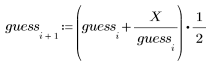
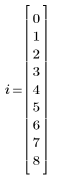 | 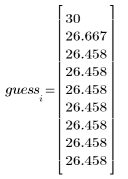 | 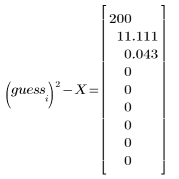 |
Встроенная функция квадратного корня дает следующий результат:
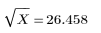
4. Постройте вектор оценок.
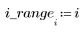
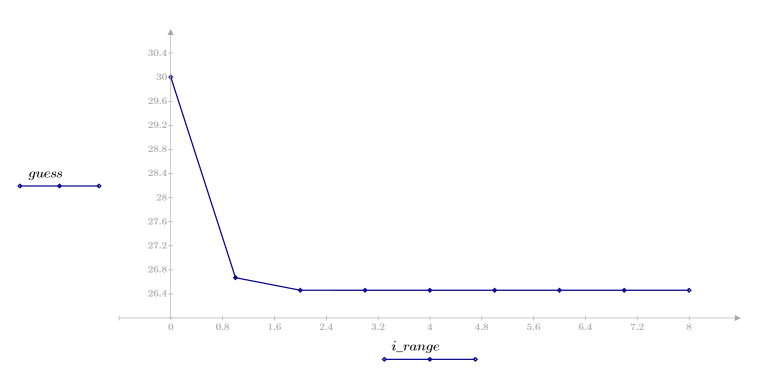
В данном случае сходимость достигается очень быстро. В других случаях можно увеличить количество итераций N в соответствии с требованиями проблемы.
Системы разностных уравнений
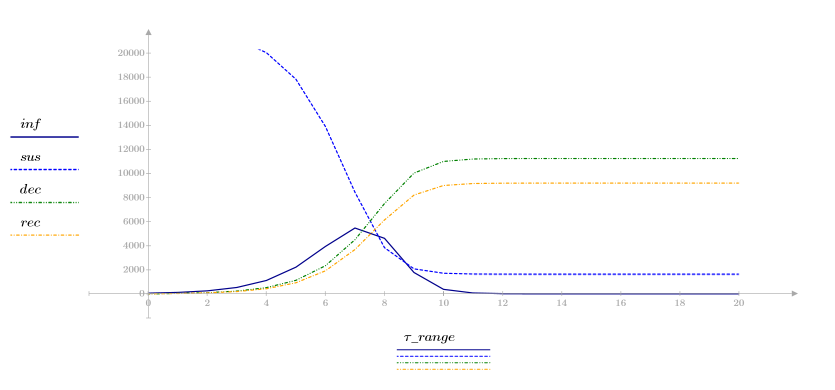
Рассмотрим модель инфекции с четырьмя переменными:
• inf — количество инфицированных особей;
• sus — количество восприимчивых;
• dec — количество умерших;
• rec — количество выздоровевших.
1. Задайте значения начальных чисел для параллельной итерации.

2. Задайте систему разностных уравнений.
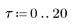
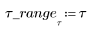
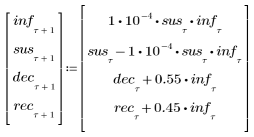
3. Постройте график четырех переменных в зависимости от времени для просмотра развития модели инфекции.
Матричные разностные уравнения
Рассмотрим марковский процесс, представляющий собой временной ряд вектора, текущее состояние которого вычисляется путем умножения предыдущего состояния на матрицу смены состояний.
1. Задайте начальное состояние вектора и матрицу смены состояний A.
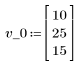

2. Задайте процесс итерации.
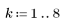
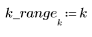
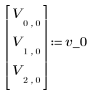
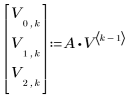
3. Рассчитайте конечное состояние вектора.
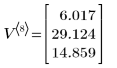
В матрице V содержится история процесса:
