Пример. Квантиль-квантильные графики

Функции > Статистика > Графическая статистика > Пример. Квантиль-квантильные графики

Используйте функцию qqplot для построения квантиль-квантильных графиков (Q-Q).

Два набора данных

Сравните квантили из двух наборов данных с помощью квантиль-квантильного графика, чтобы проверить, имеют ли они одинаковое распределение.

1. Задайте набор данных.

Щелкните для копирования этого выражения

Столбец 2 содержит номер партии, для которой проводилось измерение, а столбец 3 — измеренную прочность пластин связанного силикатного нитрата.

2. Извлеките столбцы 2 и 3.

<region id="ID0EACEBB" top="345.6" left="38.400000000000006" height="25.6" width="377.50000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="156">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">BatchData</id>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">submatrix</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Data</id>
          <real>0</real>
          <apply>
            <minus />
            <apply>
              <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">rows</id>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Data</id>
            </apply>
            <real>1</real>
          </apply>
          <real>2</real>
          <real>3</real>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

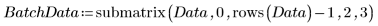
3. Вызовите функцию vlookup, чтобы разделить данные измерений для партий 1 и 2.

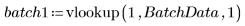
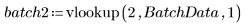
4. Вычислите первый и третий квартили каждой партии.

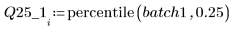
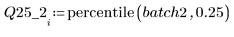
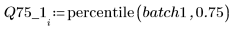
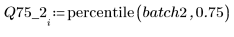
5. Постройте квантиль-квантильный график и квантили.

<region id="ID0E4KEBB" top="806.40000000000009" left="19.200000000000003" height="552" width="593.999999999999" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="178">
          <traceStyle color="#FF800080" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="179">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="180">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="181">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="182">
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="183">
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="474.799999999999" height="360" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="345" end="845">
          <axisLine position="bottom" positionticmark="-1" legendWidth="335.533333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="184">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">qq</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="185">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="186">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="187">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="188">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q25_2</id>
              </math>
              <math resultRef="189">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="190">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q75_2</id>
              </math>
              <math resultRef="191">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="192">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="193">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="345" end="845">
          <axisLine position="left" positionticmark="-1" legendWidth="95.5333333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="194">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">qq</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="195">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="196">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="197">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="198">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="199">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="200">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="201">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="202">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q25_1</id>
              </math>
              <math resultRef="203">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="204">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q75_1</id>
              </math>
              <math resultRef="205">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

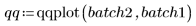
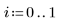
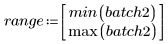
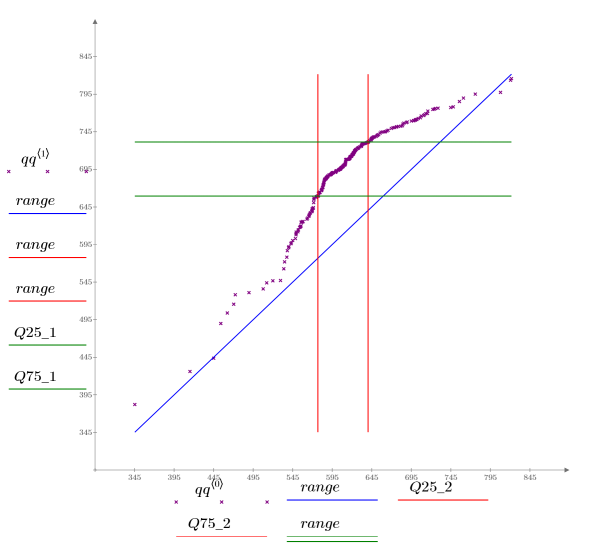
Эталонная линия 1-1 построена, чтобы подчеркнуть изменение данных.

Из квантиль-квантильного графика видно, что распределения для этих двух партий различаются, хотя значения и близки для очень малых и очень больших процентилей. Квантили для партии 1 значительно больше квантилей для партии 2, что может быть обусловлено различными условиями обработки.

Нормальное распределение

Определите, проводились ли измерения с помощью измерителя теплового потока случайным образом. Проверьте, соответствуют ли измерения нормальному распределению, путем их сравнения с нормальным распределением на квантиль-квантильном графике.

1. Задайте набор данных, описывающий тепловой поток.

2. Найдите точки данных для нормального квантиль-квантильного графика.

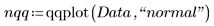
3. Найдите линию наилучшего соответствия, чтобы проверить, насколько близки квантили данных к квантилям нормального распределения.

<region id="ID0EYQEBB" top="2016.0000000000002" left="38.400000000000006" height="25.6" width="152.6866666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="234">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">BestFit</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <plus />
        <apply>
          <mult />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
        </apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">b</id>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

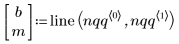
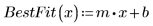
4. Постройте квантиль-квантильный график и линию наилучшего соответствия.

<region id="ID0EJSEBB" top="2092.8" left="19.200000000000003" height="312" width="590.999999999999" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="236">
          <traceStyle color="#FFFF0000" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="237">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="394.999999999999" height="235.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="9.15" end="9.4">
          <axisLine position="origin" positionticmark="5" legendWidth="91.2633333333333" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="244">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">nqq</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="245">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="239">
              <real xmlns="http://schemas.mathsoft.com/math50">9.15</real>
            </startValue>
            <secondTickValue resultRef="241">
              <real xmlns="http://schemas.mathsoft.com/math50">9.20</real>
            </secondTickValue>
            <endValue resultRef="243">
              <real xmlns="http://schemas.mathsoft.com/math50">9.35</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-3.5" end="3.5">
          <axisLine position="left" positionticmark="-1" legendWidth="157.56" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="246">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">nqq</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="247">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="248">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">BestFit</id>
                  <apply>
                    <matcol />
                    <id xml:space="preserve">nqq</id>
                    <real>0</real>
                  </apply>
                </apply>
              </math>
              <math resultRef="249">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

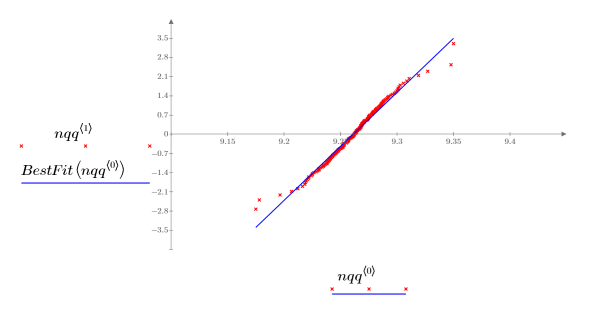
Очень близкая корреляция с эталонной линией указывает на то, что распределение выборок нормальное.

Проверка нормальности — это одна из проверок, проводимых для обнаружения отклонений.

Распределение Вейбулла

Проверьте, соответствует ли набор данных распределению Вейбулла.

1. Сохраните в векторе R напряжения пробоя электрической изоляции для кабелей, находящихся под возрастающим градиентом напряжения.

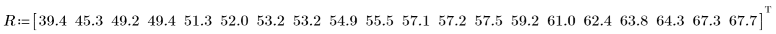
2. Постройте гистограмму данных.

<region id="ID0EVXEBB" top="2880.0000000000005" left="19.200000000000003" height="312" width="589.906666755675" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="267">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <graph-size width="470.706666755675" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="32.5" end="72.5">
          <axisLine position="origin" positionticmark="0" legendWidth="115.576666666667" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="270">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <plus />
                  <id xml:space="preserve">bins</id>
                  <real>2.5</real>
                </apply>
              </math>
              <math resultRef="271">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="269">
              <real xmlns="http://schemas.mathsoft.com/math50">37.5</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="5">
          <axisLine position="left" positionticmark="-1" legendWidth="85.6133333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="272">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">stem</id>
              </math>
              <math resultRef="273">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

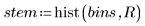
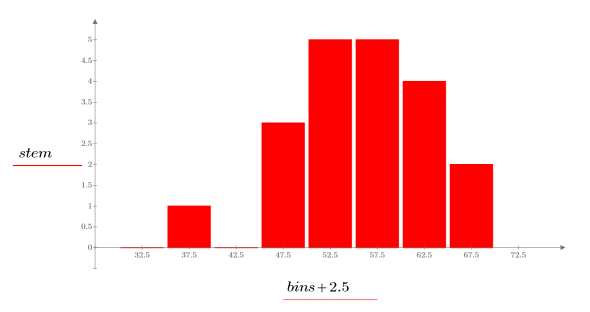
Из гистограммы видно, что данные не соответствуют нормальному распределению. Данные перекошены в одну сторону. Данные можно сравнить с распределением Вейбулла на квантиль-квантильном графике.

3. Найдите точки данных для квантиль-квантильного графика распределения Вейбулла.

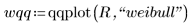
4. Найдите линию наилучшего соответствия, чтобы проверить, насколько близки квантили данных квантилям распределения Вейбулла.

<region id="ID0EK2EBB" top="3494.4000000000005" left="38.400000000000006" height="25.6" width="152.6866666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="283">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">BestFit</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <plus />
        <apply>
          <mult />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
        </apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">b</id>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

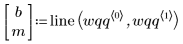
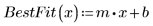
5. Постройте квантиль-квантильный график и линию наилучшего соответствия.

<region id="ID0E23EBB" top="3571.2000000000007" left="19.200000000000003" height="312" width="592.999999999999" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="285">
          <traceStyle color="#FFFF0000" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="286">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="396.999999999999" height="235.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="3.6" end="4.3">
          <axisLine position="origin" positionticmark="8" legendWidth="93.3466666666667" />
          <axisGrid>
            <gridFrequency>8</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="293">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">wqq</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="294">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="288">
              <real xmlns="http://schemas.mathsoft.com/math50">3.60</real>
            </startValue>
            <secondTickValue resultRef="290">
              <real xmlns="http://schemas.mathsoft.com/math50">3.7</real>
            </secondTickValue>
            <endValue resultRef="292">
              <real xmlns="http://schemas.mathsoft.com/math50">4.3</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-6.4" end="2.4">
          <axisLine position="left" positionticmark="-1" legendWidth="159.643333333333" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="295">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">wqq</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="296">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="297">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">BestFit</id>
                  <apply>
                    <matcol />
                    <id xml:space="preserve">wqq</id>
                    <real>0</real>
                  </apply>
                </apply>
              </math>
              <math resultRef="298">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

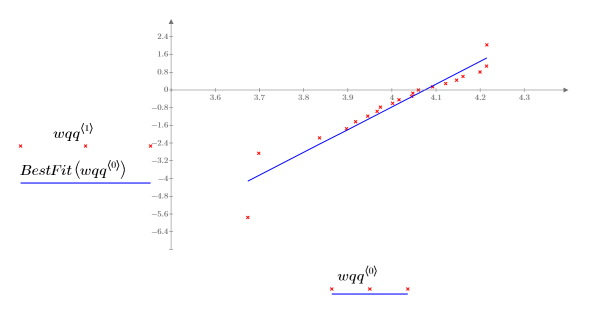
Близкая корреляция с эталонной линией указывает на то, что этот набор данных можно моделировать с помощью распределения Вейбулла.

При построении квантиль-квантильных графиков распределения Вейбулла используется логарифмическая шкала.

Справочная информация

Lawless, J.F., Statistical Methods for Lifetime Data (Статистические методы обработки ресурсных данных), 2-е изд., Wiley-Interscience, 2002.

Похожие темы

Квантиль-квантильный график

Было ли это полезно?