Пример. Обнаружение отклонения
Используйте функции Grubbs, GrubbsClassic, ThreeSigma и boxplot для обнаружения отклонений с применением трех различных методов.
1. Задайте вектор, описывающий тепловой поток.
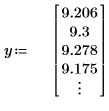
2. Постройте график данных и среднее значение данных.
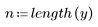
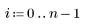
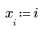
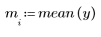
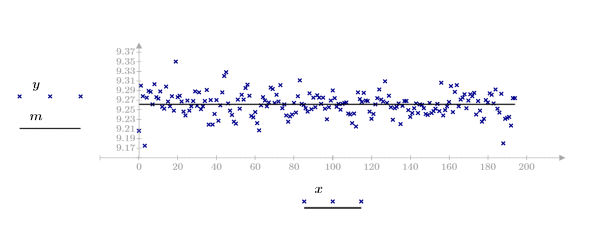
Для поиска возможных отклонений можно использовать графики разброса, однако если отклонения явно не выражены или встречаются редко, их обнаружить трудно. Можно рассчитать количественные параметры для определения точек, которые являются отклонениями.
3. Определите уровень значимости.
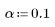
4. Вызовите функцию Grubbs для поиска отклонений в наборе данных.
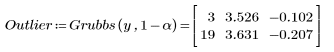
В первом столбце содержатся индексы точек, идентифицированных в качестве отклонений (их значения критерия превышают значения критерия Граббса).
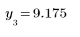
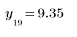
Во втором столбце приведены значения критерия для каждого отклонения (расстояние от отклонения до среднего значения в абсолютном виде).
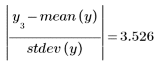
В третьем столбце приведены расстояния от значения критерия отклонения до значения критерия Граббса.
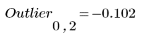
5. Вызовите функцию GrubbsClassic для поиска одной точки, которая является отклонением с наибольшей вероятностью.
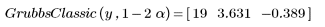
Точка с индексом 19 наиболее вероятно является отклонением. Столбцы содержат такие же данные, что и столбцы матрицы, возвращаемой функцией Grubbs.
6. Вызовите функцию ThreeSigma для поиска точек данных, которые не попадают в диапазон 3 сигма.
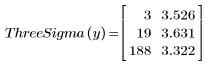
Как и в случае с функцией Grubbs, первый столбец содержит индексы, а второй — значения критерия для отклонений.
Значение критерия для всех таких точек данных превышает 3.
Если функция ThreeSigma не находит отклонений, возвращается точка, которая скорее всего может быть отклонением.
7. Вызовите функцию boxplot для обнаружения отклонений с помощью метода интерквартильного диапазона и постройте диаграмму "ящик с усами" для просмотра отклонений.
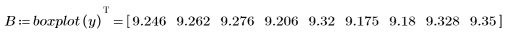
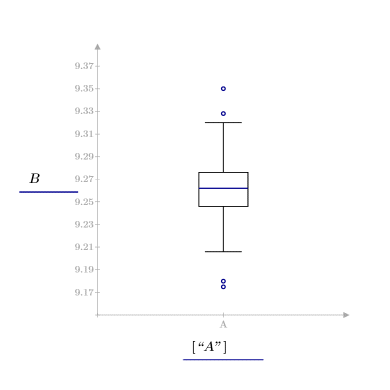
С помощью метода интерквартильного диапазона обнаружено четыре отклонения.
Можно также обнаруживать отклонения после аппроксимации данных с помощью анализа остатков.