Пример. LU-разложение матриц на множители
Используйте функцию LU, чтобы выполнить разложение на множители матрицы LU.
|
|
Во избежание логических несоответствий при выполнении логических сравнений включите Приблизительное равенство (Approximate Equality) в выпадающем списке Параметры расчета (Calculation Options).
|
LU-разложение на множители вещественной матрицы
1. Определите вещественную матрицу M1 размерности m x n так, что m > n.
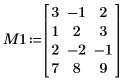
2. Используйте функцию LU, чтобы выполнить LU-разложение на множители матрицы M1.

3. Покажите, что P1 x M1 = L1 x U1.
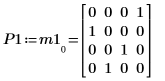 |  | 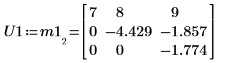 |
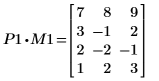 | 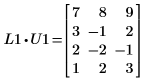 | |
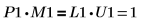 |
Отношение логически истинно.
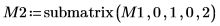 |
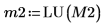 |
5. Покажите, что P2 x M2 = L2 x U2.
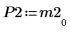 | 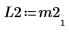 | 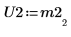 |
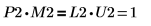 |
Отношение логически истинно.
6. Используйте функцию submatrix, чтобы извлечь матрицу M3 так, что m = n.
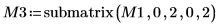 |
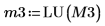 |
7. Покажите, что P3 x M3 = L3 x U3.
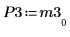 | 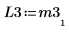 | 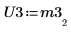 |
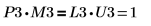 |
Отношение логически истинно.
LU-разложение на множители комплексной матрицы
1. Определите комплексную матрицу C1 с размерами m x n так, что m > n.
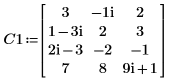
2. Используйте функцию LU, чтобы выполнить LU-разложение на множители матрицы C1.

3. Покажите, что P4 x C1 = L4 x U4.
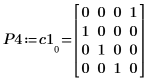 | 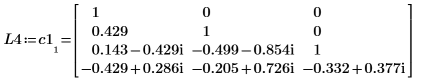 | 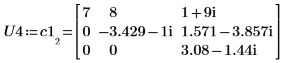 |
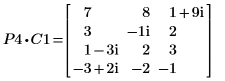 | 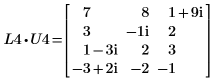 | |
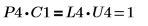 |
Отношение логически истинно.
4. Используйте функцию submatrix, чтобы извлечь матрицу C2 так, что m < n.
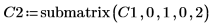 | 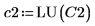 | 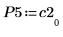 |
5. Покажите, что P5 x C2 = L5 x U5.
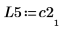 | 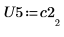 |
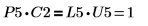 |
Отношение логически истинно.
6. Используйте функцию submatrix, чтобы извлечь матрицу C3 так, что m = n.
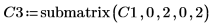
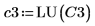
7. Покажите, что P6 x C3 = L6 x U6.
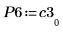 | 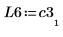 | 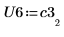 |
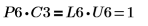 |
Отношение логически истинно.