Пример. Однофакторный ANOVA
Используйте функцию fullfact, чтобы спроектировать эксперимент, и функцию anova для анализа его результатов.
1. Задайте число факторов в эксперименте, определяющем влияние количества хлопковых волокон на прочность нового синтетического волокна.
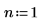
2. Задайте параметры хлопка, используемые в эксперименте.
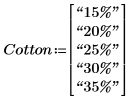
3. Используйте функцию length, чтобы определить число уровней для фактора.
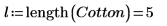
4. Вызовите функцию fullfact, чтобы создать полную матрицу плана факторного эксперимента, определяющую эксперимент и его выполнения.
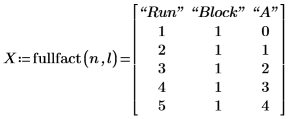
В матрице плана X столбец A определяет фактор хлопка, а его уровни показаны в кодированной форме:
Кодированные значения A | Действительные значения A |
|---|---|
0 | 15% |
1 | 20% |
2 | 25% |
3 | 30% |
4 | 35% |
5. Измерьте прочность синтетического волокна для первого выполнения, где вес хлопка составляет 15 %.
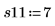
6. Получите измерения для остальных 4-х выполнений.
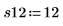
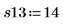
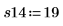
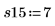
7. Вызовите функцию randomize, чтобы поменять порядок выполнения.
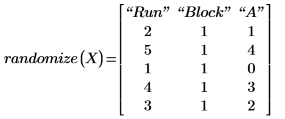
8. Повторите измерения в порядке, заданном функцией randomize.
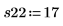
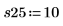
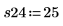
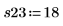
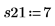
Повторение экспериментов полезно для получения усредненного значения влияния неконтролируемых переменных. Вызов функции randomize перед повторением экспериментов позволяет уменьшить порядок корреляции между входными факторами.
9. Выполните шаги 7 и 8 для всех требуемых репликаций. Занесите все измерения в матрицу Y.

Каждый столбец содержит данные для одной из репликаций, а каждая строка — данные конкретного выполнения.
10. Вызовите функцию boxplot, чтобы подготовить данные для диаграммы "ящик с усами".
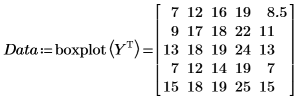
Матрица Y транспонируется, поскольку данные для каждого выполнения хранятся в ее строках, а наборы данных для функции boxplot должны быть записаны в столбцах матрицы.
11. Вызовите функцию boxplotgraph.
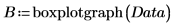
12. Создайте диаграмму "ящик с усами".
a. Постройте график данных, возвращаемых функцией boxplotgraph.
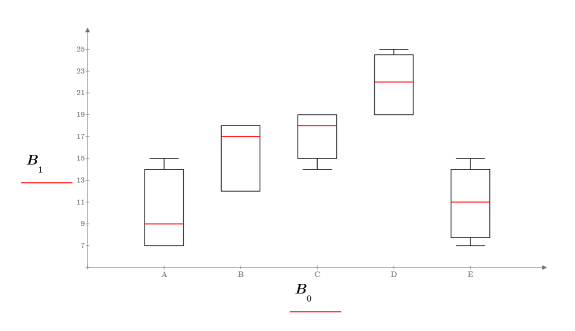
b. Создайте текстовые области с обозначениями для каждого фактора.
На диаграмме "ящик с усами" видно, что процентное соотношение хлопка влияет на предел прочности волокна при растяжении. Предел прочности волокна достигает максимума, когда вес хлопка составляет 30 % от веса волокна.
13. Вызовите функцию anova, чтобы протестировать влияние весового процента хлопка на прочность волокна при растяжении.

14. Определите r как число выполнений, а x как число повторений, а затем вычислите сумму квадратов в столбце SSE.
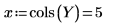
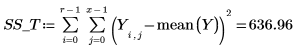
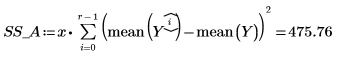
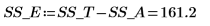
15. Определите N как общее число измерений, а затем вычислите степени свободы в столбце df.
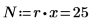
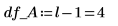
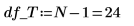
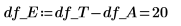
16. Вычислите среднеквадратичное значение в столбце MSE.
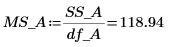
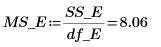
17. Вычислите F-value для фактора A.
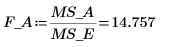
P-value в столбце P меньше 0.05, что означает, что фактор A является значимым.
18. Используйте F-value, чтобы проверить гипотезу, что фактор A является значимым. Вычислите критическое значение F для уровня значимости, равного 5 %.
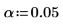
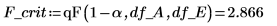
F-value для фактора A больше критического значения F, и это еще раз подтверждает, что процентное соотношение хлопка влияет на предел прочности волокна при растяжении.
Справочная информация
Montgomery, D.C., Design and Analysis of Experiments (Планирование и анализ эксперимента), 5th ed., John Wiley & Sons, New York, 2001. 62.