Функции эллиптических интегралов
Функции эллиптических интегралов представляют собой группу интегральных функций следующего вида:
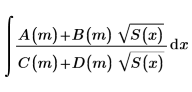
A(m) C(m), B(m) и D(m) являются полиномиальными, и S(x) является полиномиалом степени 3 или 4. Функции эллиптических интегралов полезны во многих расчетных задачах, включая электромагнетизм и гравитацию.
Можно использовать функции эллиптических интегралов полного или неполного вида. В полном виде вычисляется интеграл от 0 до 1. В полном виде вычисляется интеграл от 0 до переменной z. В Mathcad можно использовать следующие функции эллиптических интегралов:
• ellipticK - полный эллиптический интеграл первого рода
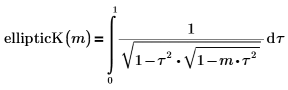
• ellipticF - неполный эллиптический интеграл первого рода
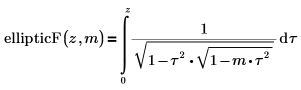
• ellipticE - полный эллиптический интеграл второго рода
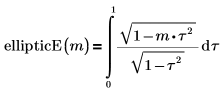
• ellipticE - неполный эллиптический интеграл второго рода
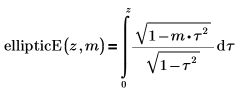
• ellipticPi - полный эллиптический интеграл третьего рода
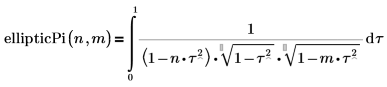
• ellipticPi - неполный эллиптический интеграл третьего рода
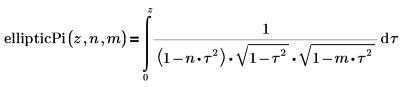
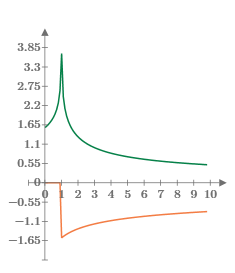
См. поведение функции ellipticK в интервале 0-10. Результатом является вещественное число, если 0<m<1, и комплексное число, если m>1.
Зеленая кривая представляет вещественные результаты, а оранжевая - комплексные результаты.
Аргументы
• m - скаляр или вектор.
• n и z - скаляры.