Сведения о начальных приближениях
Начальные приближения для всех неизвестных переменных требуются при решении систем линейных или нелинейных уравнений, а также при оптимизации функций.
• Для линейных систем начальные приближения используются только для определения размера результата решения. Их значения не важны.
В приведенных ниже блоках решения показано, как различные начальные приближения x не влияют на результат возвращаемого решения.
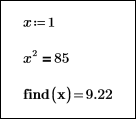 |
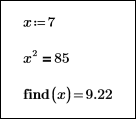 |
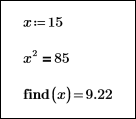 |
• В нелинейных задачах начальные приближения значительно влияют на получаемое решение. Здесь можно применить советы по выбору и изменению начальных приближений, описанные для функции root.
Определение начальных приближений
Для функций find и minerr необходимо определить неизвестные переменные при вызове функции блока решения. Начальные приближения должны иметь такие же имена, как и неизвестные переменные.
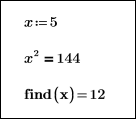
Для функций minimize и maximize неизвестные переменные понятны, поскольку они являются аргументами целевой функции (функции оптимизации). Однако в функции блока решения необходимо задать начальные приближения для всех неизвестных переменных. Порядок, в котором начальные приближения передаются в minimize, должен совпадать с порядком аргументов целевой функции. Здесь a — это начальное приближение для θ, а b — начальное приближение для φ:

Вещественные или комплексные начальные приближения
В блоках решения сначала обрабатываются заданные ограничения, а для исключения ошибок и определения области решения используются начальные приближения.
Если значения начальных приближений являются вещественными и при вычислении левых и правых сторон ограничений с использованием начальных приближений получаются только вещественные значения или матрицы вещественных значений, искомое решение является вещественным. В противном случае решатель может возвратить комплексное решение.