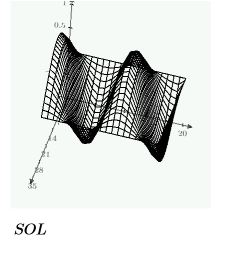
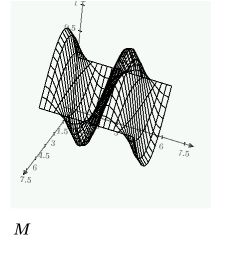
例: ソルブブロック内の PDE
「ソルブブロック」内の偏微分方程式 (PDE) と偏微分方程式ソルバー「numol」を使用して、波動方程式の解を比較します。
PDE ソルブブロック
次の 1 次元波動方程式を解くには、
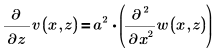
次の制約条件を使用します。
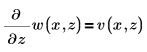
1 つ目の方程式を 2 つの偏微分方程式の連立方程式として解くには、PDE ソルブブロックを設定します。
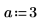
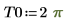
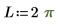
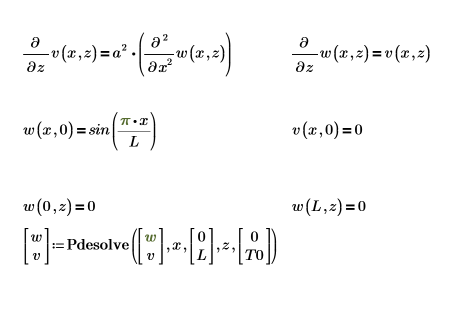
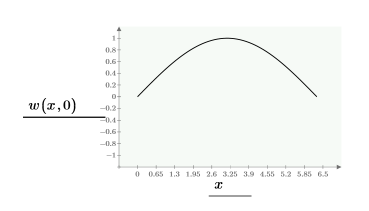
境界上の単一の解を次に示します。
上記で定義した制約条件を使用して、CreateMesh 関数で 3 次元的にプロットする解のグリッドを作成します。
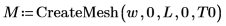
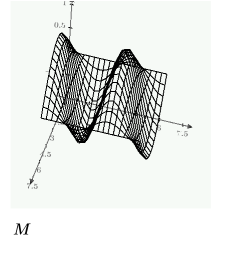
numol の使用
コマンドラインソルバー「numol」を解くことができます。これは、計算をプログラムに含める場合に特に便利です。
システム内の偏微分方程式と代数制約条件の数を定義します。
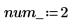
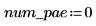
PDE の右辺を評価する関数は、長さ num_pde + num_pae (部分的代数方程式) のベクトルです。この場合、関数は連立方程式です。同様に、境界条件は長さ num_pde + num_pae の列ベクトルとして定義されます。
PDE のベクトルの式:
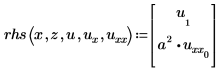
したがって、u1=v は上記のように定義され、u0=w です。
初期条件のベクトル:
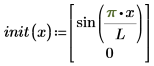
各左辺が未知関数ベクトル u の 1 階時間微分であると仮定します。関数の変数は x (空間) と t (時間) です。解は u で、連立方程式の解のベクトルでもある場合があります。ここで、ux はベクトル内の各解 u の 1 次導関数で、uxx は 2 次空間導関数です。
ベクトルの下付き文字を使用して、u、ux、および uxx の個々のエントリに対処しなければなりません。
境界条件のベクトルには、3 つのタイプの行を使用できます。各行は以下のいずれかによって決定されます。
• rhs には、2 次空間導関数が含まれています。積分領域の各辺につき 1 つずつ、合計 2 つの境界条件 (ディリクレの "D" またはノイマンの "N" のいずれか) が必要です。
• rhs には、1 次空間導関数が含まれています。積分領域の左辺または右辺にディリクレ境界条件があり、もう一方の辺は "NA" です。
• ベクトルに空間導関数が含まれていない場合、境界条件は不要です。
左側および右側の境界の境界条件は、以下の規則に従います。
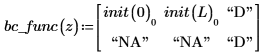
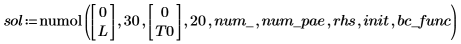
numol の結果は、空間内の各点を行として、時間内の各点を列として表す行列です。これにより、一度に 1 つの列を取り上げることができるようにし、単一時点ですべての空間にわたって解を表すことで、解のビジュアリゼーションが容易になります。連立方程式を解くとき、各未知関数の解行列が前の行列の辺に追加されます。
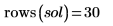
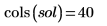
現在の例では、各関数につき 20 個の時点があるので、行列には 40 列が含まれています。1 つ目の解 u0 を選びます。
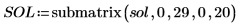
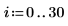
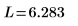
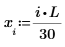
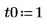
numol と Pdesolve の比較
点 t0 で numol 解と Pdesolve 解を比較します。
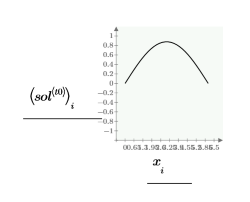
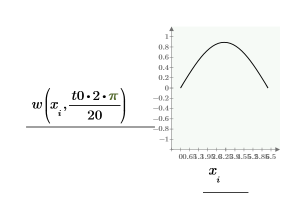
解のグリッドを空間および時間の値と比較します。