Esempio: utilizzo di unità di misura con le funzioni di interpolazione polinomiale

Funzioni > Analisi dati > Interpolazione e predizione > Esempio: utilizzo di unità di misura con le funzioni di interpolazione polinomiale

1. Definire due vettori di input e una variabile indipendente.

Fare clic per copiare questa espressione

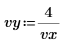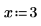2. Definire le unità di misura.

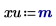
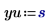
3. Valutare i vettori di input e la variabile di input.

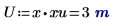L'unità di misura della variabile indipendente U deve corrispondere all'unità di misura del vettore del primo argomento.

Interpolazione polinomiale

1. Utilizzare la funzione polyint per valutare la funzione di interpolazione in corrispondenza dei valori della variabile indipendente specificati.

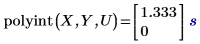
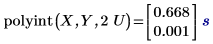
La ricerca di U in un vettore di input X restituisce una corrispondenza e il valore esatto corrispondente nel vettore Y è 1.333 con un errore zero. 2U, tuttavia, non ha una corrispondenza esatta in X e pertanto restituisce un valore interpolato con un errore diverso da zero.

2. Utilizzare la funzione length per determinare la lunghezza dei vettori di input, quindi creare un breve programma per valutare le funzioni di interpolazione in corrispondenza di punti diversi. Visualizzare i punti interpolati nella prima colonna e i valori di errore nella seconda colonna.

<region id="ID0ELOMU" actualWidth="485.86333333333334" actualHeight="197.304" top="1075.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="45">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">M</id>
 <eval>
 <program>
 <for>
 <id labels="VARIABLE" xml:space="preserve">u</id>
 <range>
 <real>0</real>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L</id>
 </range>
 <program>
 <for>
 <id labels="VARIABLE" xml:space="preserve">v</id>
 <range>
 <real>0</real>
 <real>1</real>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">M</id>
 <sequence>
 <id labels="*" xml:space="preserve">u</id>
 <id labels="*" xml:space="preserve">v</id>
 </sequence>
 </apply>
 <apply>
 <indexer />
 <parens>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyint</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <apply>
 <mult />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">u</id>
 <id labels="UNIT" xml:space="preserve">m</id>
 </apply>
 </sequence>
 </apply>
 </parens>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
 </apply>
 </localDefine>
 </program>
 </for>
 </program>
 </for>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 </program>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

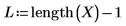
La variabile u deve essere uno scalare e l'unità di misura m viene aggiunta come parte dell'argomento della funzione.

3. Salvare i punti di interpolazione e i valori di errore in due vettori separati.

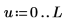
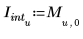
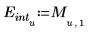
4. Tracciare il grafico dei punti di interpolazione insieme all'inviluppo dell'errore.

<region id="ID0EUSMU" actualWidth="576" actualHeight="307.2" top="1401.6000000000001" left="38.400000000000006" height="307.2" width="576" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="49">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="50">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace resultRef="51">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="418.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="origin" positionticmark="0" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <secondTickValue resultRef="52">
 <real xmlns="http://schemas.mathsoft.com/math50">0.9</real>
 </secondTickValue>
 <endValue resultRef="53">
 <real xmlns="http://schemas.mathsoft.com/math50">9</real>
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="12">
 <axisLine position="origin" positionticmark="0" legendWidth="126.556666666667" />
 <axisGrid>
 <gridFrequency>13</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <plus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <minus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

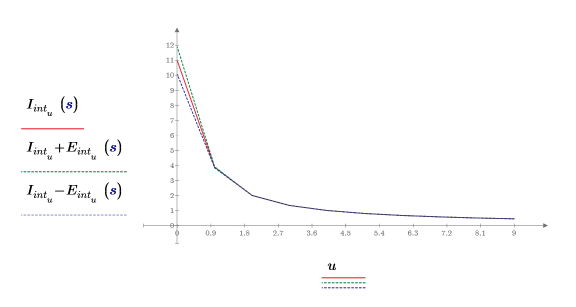
L'errore inizia come relativamente ingente e quindi diventa trascurabile dopo il secondo punto di interpolazione.

Iterazione polinomiale

1. Utilizzare la funzione polyiter per valutare la funzione di iterazione in corrispondenza del valore della variabile indipendente specificato, del numero di iterazioni massime e della tolleranza.

<region id="ID0EZUMU" actualWidth="261.85" actualHeight="62.800000000000004" top="1900.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="54">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U</id>
 <real>2</real>
 <apply>
 <scale />
 <real>0.1</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

<region id="ID0EHVMU" actualWidth="261.85" actualHeight="62.800000000000004" top="1977.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="55">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U</id>
 <real>5</real>
 <apply>
 <scale />
 <real>0.1</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

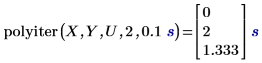
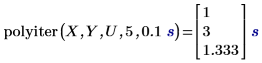
• L'algoritmo si interrompe se le ultime due stime iterate del punto dati accettano di rimanere entro il valore di tolleranza oppure se il numero di iterazioni raggiunge il numero massimo consentito di iterazioni.

• Il primo risultato indica che la funzione di iterazione non è riuscita a convergere dopo aver raggiunto il numero massimo consentito di due iterazioni e pertanto ha restituito l'elemento corrispondente in un vettore Y.

• Il secondo risultato indica che la funzione di iterazione è riuscita a convergere dopo la terza iterazione e non ha raggiunto il numero massimo consentito di cinque iterazioni.

2. Utilizzare un breve programma per valutare la funzione di iterazione in corrispondenza di dieci punti diversi. Utilizzare la funzione augment per aggiungere il valore di errore nella quarta colonna della matrice restituita, in cui vengono visualizzati lo stato di unione nella prima colonna, il numero di iterazioni utilizzate nella seconda colonna e i valori iterati nella terza colonna.

<region id="ID0E21MU" actualWidth="487.13666666666654" actualHeight="200.2" top="2284.8" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="56">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <function>
 <id labels="VARIABLE" xml:space="preserve">
 P<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <boundVars>
 <id labels="VARIABLE" xml:space="preserve">ord</id>
 <id labels="VARIABLE" xml:space="preserve">err</id>
 </boundVars>
 </function>
 <program>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">order</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ord</id>
 </localDefine>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">error</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">err</id>
 </localDefine>
 <for>
 <id labels="VARIABLE" xml:space="preserve">u</id>
 <range>
 <real>0</real>
 <apply>
 <minus />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">length</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 </apply>
 <real>1</real>
 </apply>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">K</id>
 <id labels="*" xml:space="preserve">u</id>
 </apply>
 <apply>
 <mult />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">error</id>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </localDefine>
 <for>
 <id labels="VARIABLE" xml:space="preserve">v</id>
 <range>
 <real>0</real>
 <real>2</real>
 </range>
 <program>
 <localDefine>
 <apply>
 <indexer />
 <id labels="VARIABLE" xml:space="preserve">N</id>
 <sequence>
 <id labels="*" xml:space="preserve">u</id>
 <id labels="*" xml:space="preserve">v</id>
 </sequence>
 </apply>
 <apply>
 <indexer />
 <parens>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">polyiter</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
 <apply>
 <mult />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">u</id>
 <id labels="UNIT" xml:space="preserve">m</id>
 </apply>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">order</id>
 <apply>
 <scale />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">error</id>
 <id labels="UNIT" xml:space="preserve">s</id>
 </apply>
 </sequence>
 </apply>
 </parens>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
 </apply>
 </localDefine>
 </program>
 </for>
 </program>
 </for>
 <localDefine>
 <id labels="VARIABLE" xml:space="preserve">Z</id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">augment</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">K</id>
 </sequence>
 </apply>
 </localDefine>
 <return>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Z</id>
 </return>
 </program>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

3. Salvare i punti di interpolazione e i valori di errore in vettori separati.

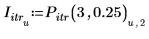
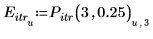
4. Tracciare il grafico dei punti di iterazione per 3 iterazioni e un errore 0.25.

<region id="ID0EJ5MU" actualWidth="577" actualHeight="307.20000000000005" top="2707.2000000000003" left="38.400000000000006" height="307.20000000000005" width="577" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="59">
 <traceStyle color="#FFED1D2F" symbol="filledRectangle" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="60">
 <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace resultRef="61">
 <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="419.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="bottom" positionticmark="-1" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>10</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <secondTickValue resultRef="62">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0.25" end="3.55">
 <axisLine position="origin" positionticmark="0" legendWidth="123.37" />
 <axisGrid>
 <gridFrequency>12</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <plus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <minus />
 <apply>
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 <apply>
 <indexer />
 <id xml:space="preserve">
 E<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

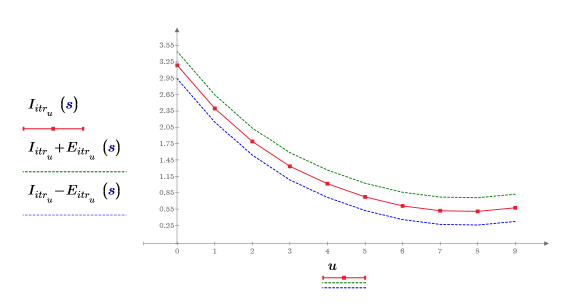
L'errore è costante in corrispondenza di ogni punto di interpolazione.

5. Confrontare i risultati restituiti dell'interpolazione e dell'iterazione quando il numero massimo di iterazioni è impostato su 3 e l'errore è impostato su 0.25.

<region id="ID0E46MU" actualWidth="576.60000000000014" actualHeight="287.99999999999994" top="3129.6000000000004" left="38.400000000000006" height="287.99999999999994" width="576.60000000000014" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="63">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="64">
 <traceStyle color="#FF068149" symbol="filledRectangle" line-weight="2" line-style="DashDotDot">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="457.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="origin" positionticmark="0" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="12">
 <axisLine position="origin" positionticmark="0" legendWidth="81.1466666666667" />
 <axisGrid>
 <gridFrequency>13</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

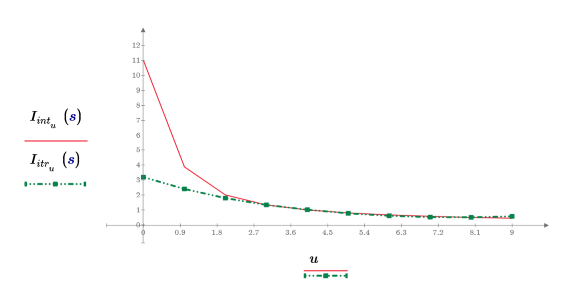
6. Mostrare che il risultato dell'interpolazione è identico a quello dell'iterazione quando il numero di iterazioni è impostato su un valore elevato e l'errore è impostato su zero.

<region id="ID0E2BNU" actualWidth="576.6" actualHeight="288" top="3571.2000000000007" left="38.400000000000006" height="288" width="576.6" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="66">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="67">
 <traceStyle color="#FF068149" symbol="filledRectangle" line-weight="2" line-style="DashDotDot">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="457.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="9">
 <axisLine position="origin" positionticmark="0" legendWidth="61.21" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">u</id>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="12">
 <axisLine position="origin" positionticmark="0" legendWidth="87.5333333333333" />
 <axisGrid>
 <gridFrequency>13</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">int</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math>
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">
 I0<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">itr</Subscript>
 </id>
 <id xml:space="preserve">u</id>
 </apply>
 </math>
 <math>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

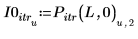
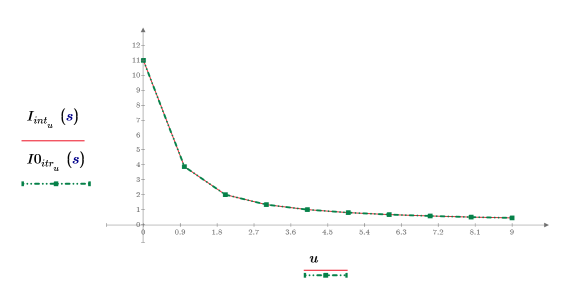
Il numero massimo di iterazioni deve essere minore della lunghezza dei vettori di input.

Argomenti correlati

Interpolazione polinomiale

È stato utile?