Esempio: segnali e relativa classificazione

Funzioni > Elaborazione dei segnali > Segnali e sistemi > Esempio: segnali e relativa classificazione

Un segnale è una funzione o un insieme di dati che rappresenta una quantità fisica o una variabile. In genere, il segnale contiene informazioni sul comportamento di un fenomeno fisico, ad esempio il flusso di corrente elettrica attraverso una resistenza, onde sonore di un sonar che si propagano sott'acqua o terremoti. In matematica, un segnale è rappresentato da una funzione di una variabile indipendente t, che in genere rappresenta il tempo. Un segnale è pertanto indicato come x(t).

Segnali a tempo continuo e discreto

Un segnale x(t) è un segnale a tempo continuo se t è una variabile continua. Se t è una variabile discreta, ovvero x(t) viene definito in tempi discreti, x(t) è un segnale a tempo discreto, spesso indicato come x(n), dove n è un numero intero. Un segnale a tempo discreto x(n) può rappresentare un fenomeno per il quale la variabile indipendente è inerentemente discreta, ad esempio il valore di chiusura giornaliero di una quotazione in borsa, oppure può essere ottenuto tramite campionamento di un segnale a tempo continuo, x(t), a t = nT, dove T è il periodo di campionamento.

Gli esempi seguenti riguardano principalmente segnali a tempo discreto. Di seguito sono disponibili alcuni esempi di segnali a tempo discreto incontrati di frequente.

Segnale a gradino unitario

1. Definire la funzione a gradino unitario utilizzando la funzione a gradino di Heaviside.

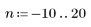
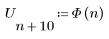
La funzione a gradino di Heaviside stabilisce che f(0)=0,5

2. Definire l'intervallo e tracciare il grafico della funzione a gradino unitario.

Fare clic per copiare questa espressione

<region id="ID0EWFM2" top="528" left="24" width="600" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FF0000FF" symbol="circle" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">n_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="3" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">U</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

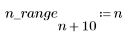
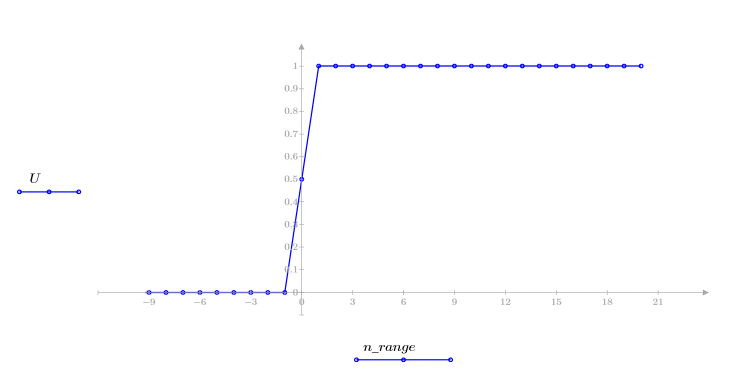
Segnale a impulso unitario

1. Definire la funzione impulso di Dirac.

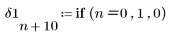
2. Tracciare il grafico della funzione impulso di Dirac.

<region id="ID0EDJM2" top="984" left="24" width="596" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">n_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="3" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">δ1</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

3. Impostare un valore di k per spostare l'impulso di k campioni a destra.

<region id="ID0EPLM2" top="1416" left="24" width="596" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">n_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="3" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">δ2</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Segnale sinusoidale

1. Impostare la frequenza.

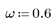
2. Definire la funzione sinusoidale.

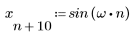
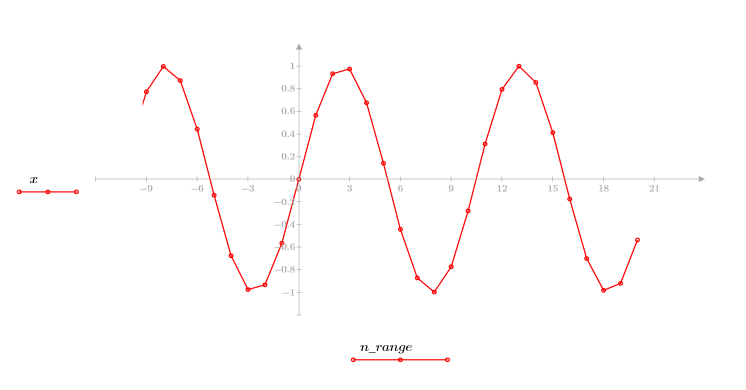
3. Tracciare il grafico della funzione sinusoidale.

<region id="ID0EMQM2" top="1944" left="24" width="597" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FFFF0000" symbol="circle" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="ticknumberlock" positionticmark="5" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">n_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="3" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Segnale esponenziale

1. Impostare il fattore alfa.

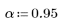
2. Definire la funzione esponenziale.

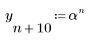
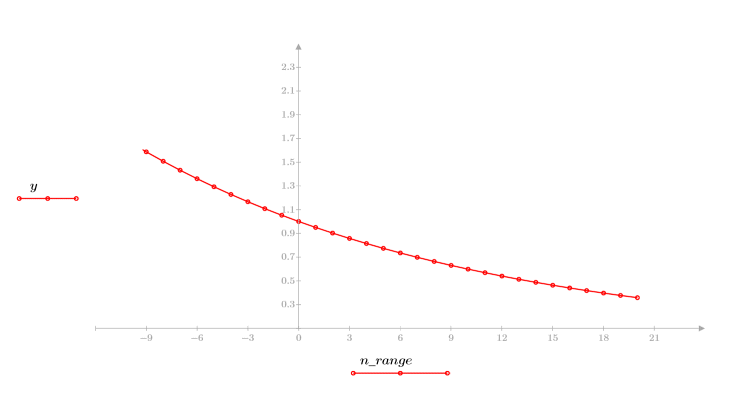
3. Tracciare un grafico della funzione esponenziale.

<region id="ID0EJVM2" top="2592" left="24" width="597" height="322.343997192383" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FFFF0000" symbol="circle" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="bottom" positionticmark="-1" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">n_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="3" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <real xmlns="http://schemas.mathsoft.com/math50">2.0</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Sinusoide con decadimento esponenziale

Tracciare il grafico della funzione risultante dal prodotto della funzione sinusoidale per la funzione esponenziale.

<region id="ID0ETWM2" top="3096" left="24" width="596" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FF008000" symbol="circle" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="4" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">n_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="3" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">z</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

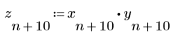
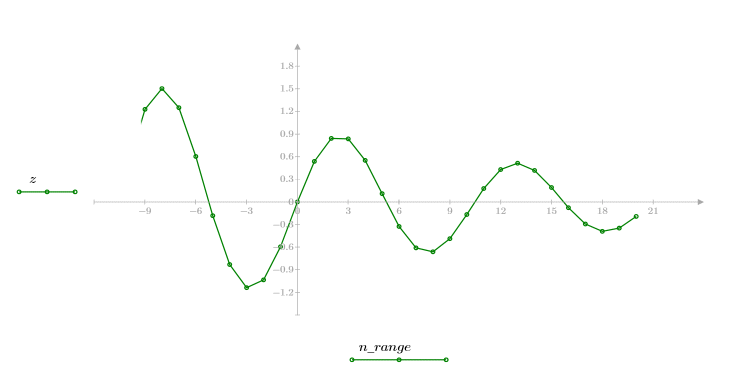
Il risultato è una funzione sinusoidale con decadimento esponenziale.

Segnali analogici e digitali

Se un segnale a tempo continuo x(t) può accettare un solo valore in un intervallo a tempo continuo, x(t) è detto segnale analogico. Se un segnale a tempo discreto x(n) può accettare solo un numero finito di valori distinti, è detto segnale digitale. Per convertire un segnale analogico in segnale digitale, è necessario campionare e quantizzare il segnale analogico.

Segnali reali e complessi

Un segnale x(t) è un segnale reale se i suoi valori sono numeri reali. Analogamente, un segnale x(t) è un segnale complesso se i suoi valori sono numeri complessi. Utilizzare le funzioni phase e phasecor per modificare segnali complessi.

Segnali deterministici e casuali

I segnali deterministici sono quelli i cui valori sono completamente specificati in ogni determinato momento nel tempo. È pertanto possibile modellare un segnale deterministico tramite una funzione nota di tempo x(t). I segnali casuali sono invece segnali che possono accettare valori casuali in qualsiasi momento nel tempo. I segnali casuali possono essere caratterizzati solo statisticamente. Le funzioni relative ai generatori di rumore whiten, gaussn e onefn sono progettate per produrre segnali pseudocasuali caratterizzati da parametri statistici definiti dall'utente.

Argomenti correlati

Quantizzazione di un segnale

È stato utile?