Esempio: finestratura del segnale
Utilizzare le funzioni seguenti per eseguire la finestratura del segnale:
Risposta all'impulso passa basso ideale/troncata
1. Definire la risposta all'impulso h di un filtro passa basso ideale con frequenza di taglio normalizzata 0.15.
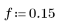
2. Definire la risposta all'impulso.
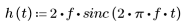
Poiché un filtro realizzabile, di lunghezza finita, deve avere una risposta all'impulso finita, questa risposta ideale viene troncata a un numero gestibile di termini.
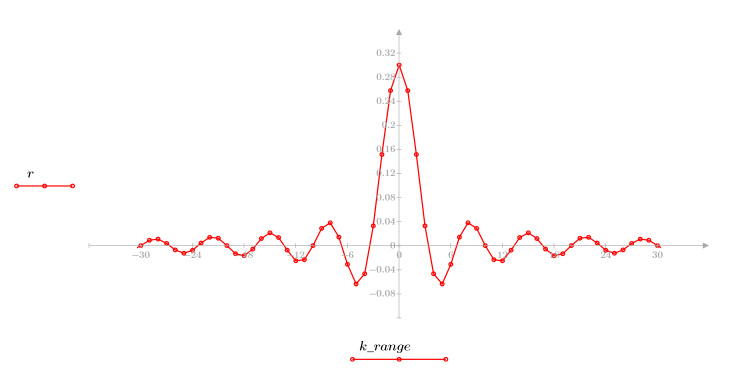
3. Per controllare l'effetto del troncamento diretto senza finestratura nella risposta in frequenza, definire un filtro di lunghezza N costituito semplicemente dagli N termini centrali della risposta ideale, spostato in modo da rendere il filtro casuale.
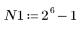
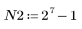
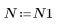
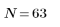
Per esercitarsi, impostare N su N2 e osservare l'effetto dell'aumento del numero di termini negli esempi seguenti.
4. Applicare la funzione di risposta all'impulso all'intervallo di termini e tracciare il grafico della funzione risultante.
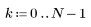
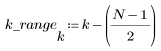
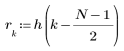
5. Calcolare la risposta in frequenza per questo segnale troncato utilizzando la funzione gain, ma prima definire la gamma di frequenza (multipli della frequenza di campionamento).
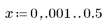
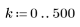
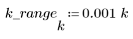
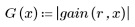
6. Raccogliere le grandezze discrete della funzione gain in un nuovo array.
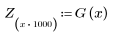
7. Trovare la grandezza massima di G e la frequenza corrispondente.
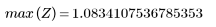
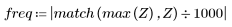
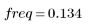
Quando il numero di termini è uguale a N1=63, il rendimento massimo di 1,083 si ottiene con una frequenza freq=0,134.
Quando il numero di termini è uguale a N2=127, il rendimento massimo di 1,092 si ottiene con una frequenza freq=0,142, avvicinandosi pertanto al limite della banda.
Con una frequenza freq=0,2 il rendimento scende quasi a zero. Confrontare il rendimento intorno a questa frequenza in ognuno degli esempi seguenti.
8. Tracciare il grafico della funzione gain nell'intervallo definito e mostrare la frequenza con cui la grandezza raggiunge il valore massimo.
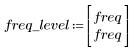
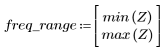
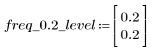
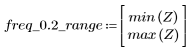
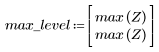
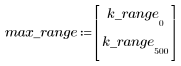
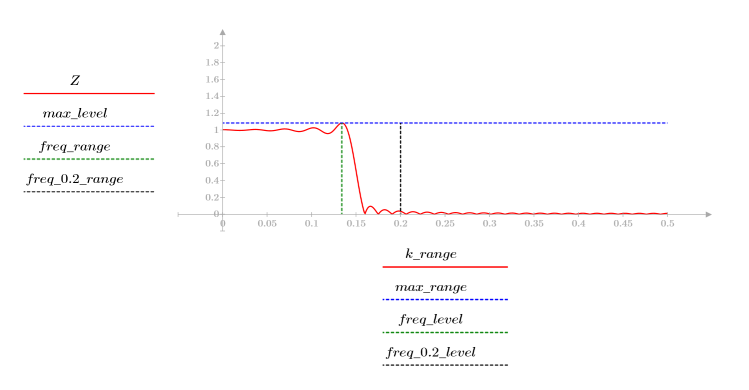
La sovraelongazione al limite della banda passante è nota come fenomeno di Gibbs. Aumentando l'ordine del filtro N da N1=63 a N2=127 nell'esempio precedente, la sovraelongazione si avvicina al limite della banda senza diminuzione della relativa ampiezza.
La transizione da 1 a 0 diventa più nitida con l'aumentare dei valori dell'ordine del filtro N.
Un metodo per produrre una risposta in frequenza più appropriata consiste nell'eseguire la finestratura per la risposta all'impulso ideale, in modo che la transizione a 0 ai limiti della risposta all'impulso del filtro sia più uniforme. Le finestre vengono moltiplicate termine per termine con un vettore di risposta r.
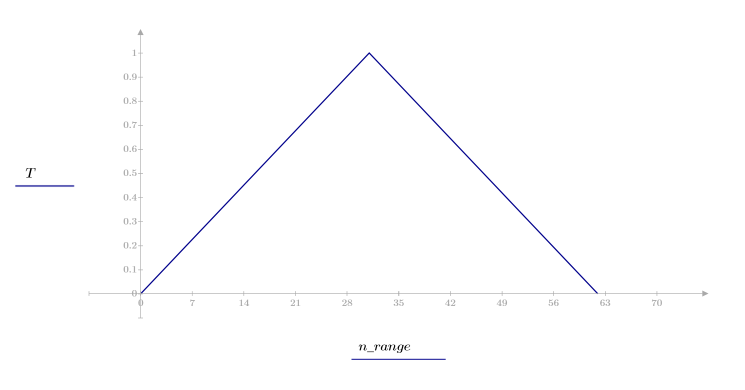
Finestra triangolare
La funzione triangular restituisce la finestra triangolare, o di Bartlett, di larghezza N.
L'elemento j-esimo del vettore risultante è determinato dalla formula riportata di seguito.
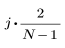
per
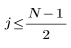
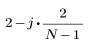
per
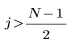
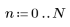
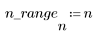
1. Applicare la funzione al filtro di ordine N e tracciare un grafico del vettore risultante.
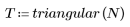
2. Calcolare la risposta all'impulso finestrato.
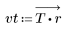
3. Utilizzare la funzione gain per calcolare il rendimento in dB di questo filtro, con coefficienti vt, a una frequenza di k/1000 e per tracciare il relativo grafico.
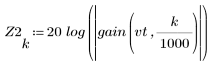
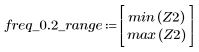
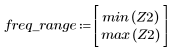
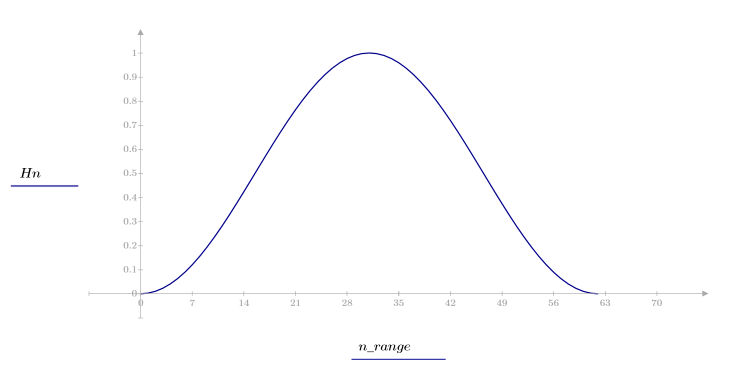
Finestra di Hanning
La funzione hanning restituisce la finestra di Hanning di larghezza N.
Il k-esimo elemento del vettore risultante è determinato dalla formula riportata di seguito.
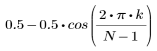
1. Applicare la funzione al filtro di ordine N e tracciare un grafico del vettore risultante.
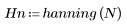
2. Calcolare la risposta all'impulso finestrato.
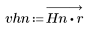
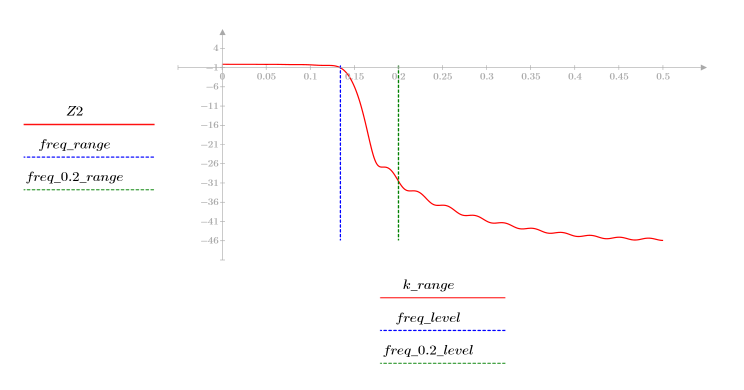
3. Utilizzare la funzione gain per calcolare il rendimento in dB di questo filtro, con coefficienti vhn, a una frequenza di k/1000 e per tracciare il relativo grafico.
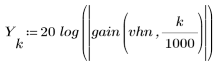
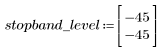
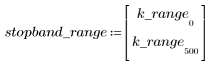
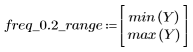
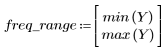
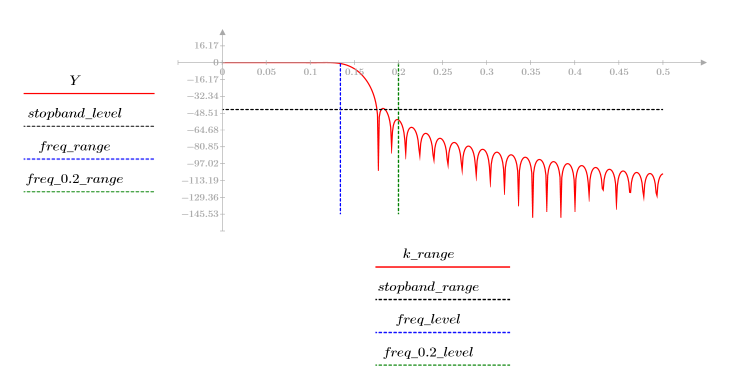
L'ondulazione della banda di reiezione è di circa -45 dB.
Finestra di Hamming
La funzione hamming restituisce la finestra di Hamming di larghezza N.
Il k-esimo elemento del vettore risultante è determinato dalla formula riportata di seguito.
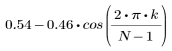
1. Applicare la funzione al filtro di ordine N e tracciare un grafico del vettore risultante.
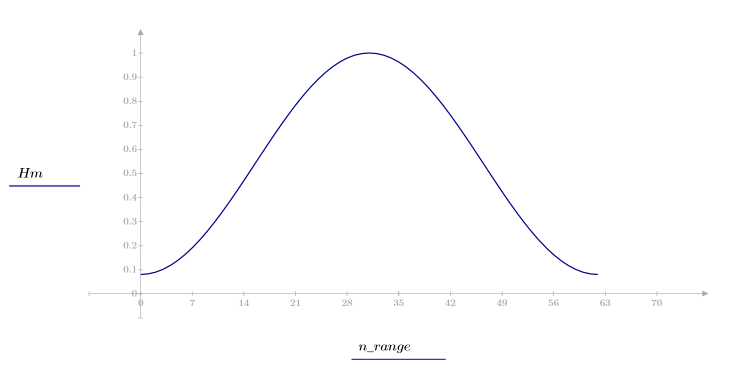
2. Calcolare la risposta all'impulso finestrato.
3. Utilizzare la funzione gain per calcolare il rendimento in dB di questo filtro, con coefficienti vhm, a una frequenza di k/1000 e per tracciare il relativo grafico.
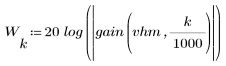
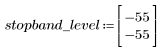
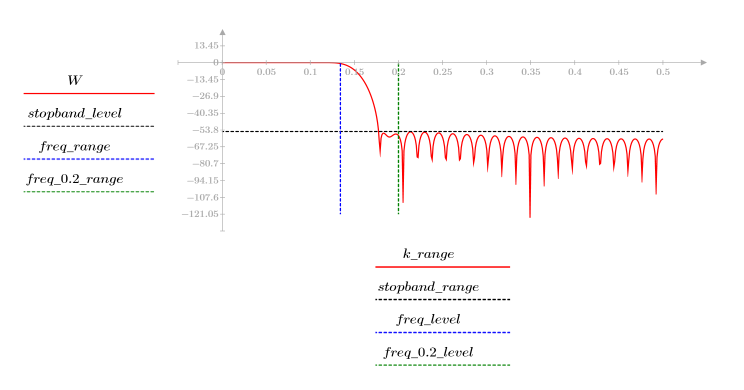
L'ondulazione della banda di reiezione è di circa -55 dB.
Finestra di Blackman
La funzione blackman restituisce la finestra di Blackman di larghezza N.
Il k-esimo elemento del vettore risultante è determinato dalla formula riportata di seguito.
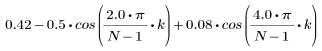
1. Applicare la funzione al filtro di ordine N e tracciare il grafico del vettore risultante.
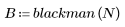
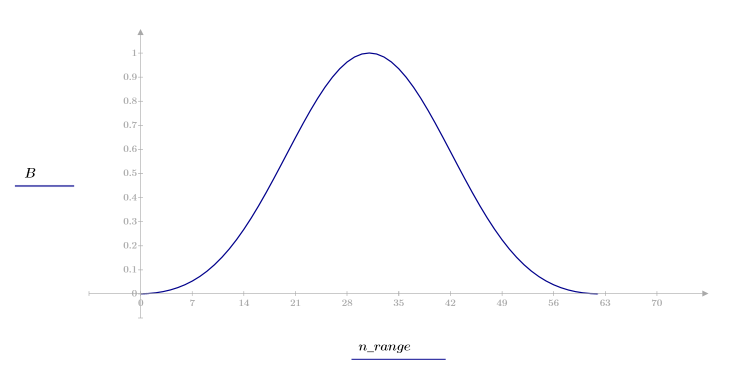
2. Calcolare la risposta all'impulso finestrato.
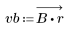
3. Utilizzare la funzione gain per calcolare il rendimento in dB di questo filtro, con coefficienti vb, a una frequenza di k/1000 e per tracciare il relativo grafico.
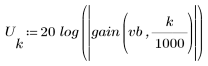
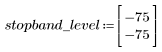
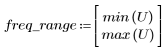
L'ondulazione della banda di reiezione è di circa -75 dB.
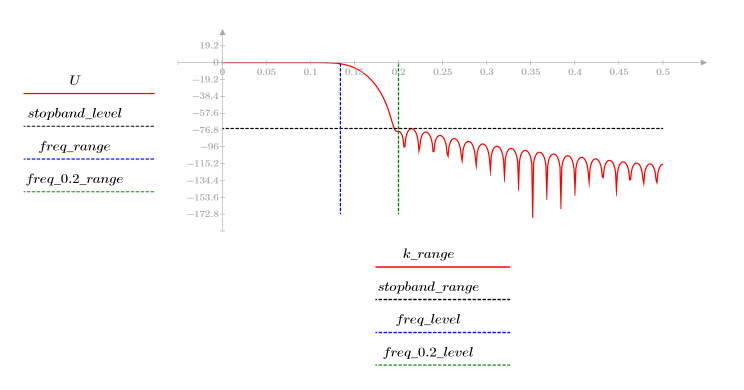
Finestra di Nuttall
La funzione nuttall restituisce la finestra di Nuttall di larghezza N.
Il k-esimo elemento del vettore risultante è determinato dalla formula riportata di seguito.
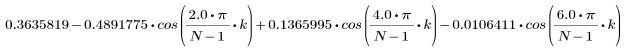
1. Applicare la funzione al filtro di ordine N e tracciare un grafico del vettore risultante.
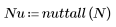
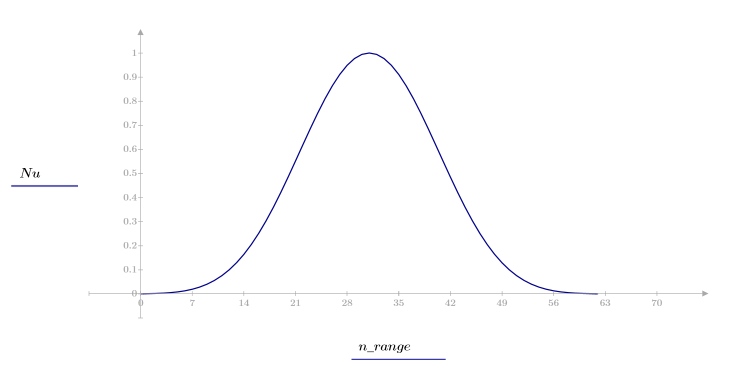
2. Calcolare la risposta all'impulso finestrato.
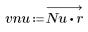
3. Utilizzare la funzione gain per calcolare il rendimento in dB di questo filtro, con coefficienti vnu, a una frequenza di k/1000 e per tracciare il relativo grafico.
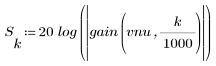
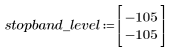
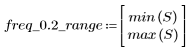
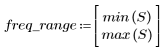
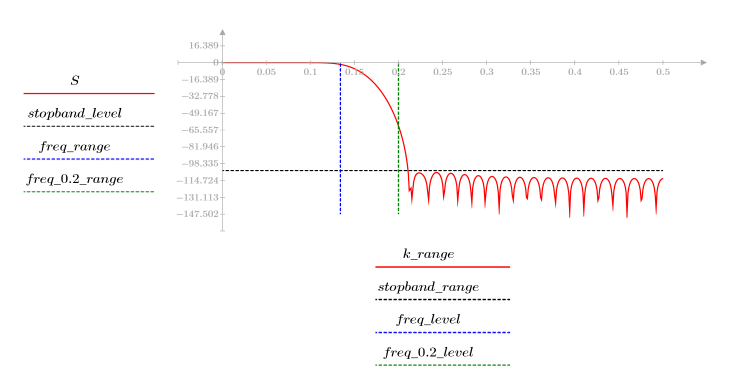
L'ondulazione della banda di reiezione è di circa -105 dB.
Finestra rettangolare rastremata
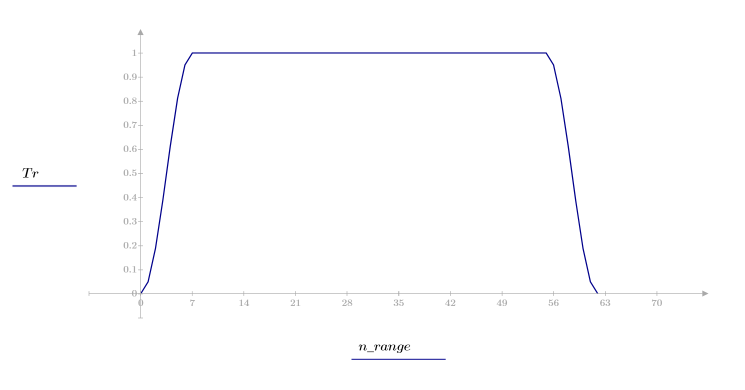
La funzione taprect restituisce la finestra rettangolare rastremata di larghezza N.
Questa finestra è orizzontale nella parte centrale a un'altezza di 1 con estremità assottigliate formate da curve di coseno. Per il lato destro e sinistro vengono utilizzati i valori:
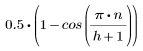
dove
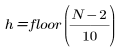
e n va da 0 a h.
1. Applicare la funzione al filtro di ordine N e tracciare un grafico del vettore risultante.
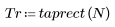
2. Calcolare la risposta all'impulso finestrato.
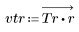
3. Utilizzare la funzione gain per calcolare il rendimento in dB di questo filtro, con coefficienti vtr, a una frequenza di k/1000 e per tracciare il relativo grafico.
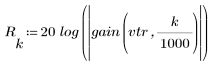
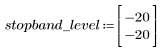
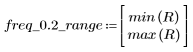
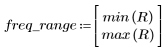
Finestra gaussiana
La funzione gaussian restituisce la finestra gaussiana di larghezza N e parametro a. Il numero è un numero reale proporzionale all'inverso della varianza gaussiana e deve soddisfare la condizione 2 < a < 20.
Il k-esimo elemento del vettore risultante è determinato dalla formula riportata di seguito.
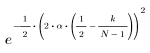
1. Applicare la funzione al filtro di ordine N e tracciare un grafico del vettore risultante.
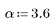
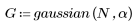
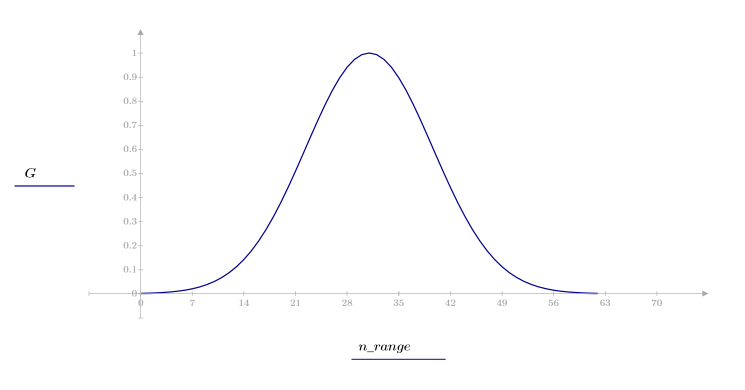
2. Calcolare la risposta all'impulso finestrato.
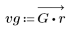
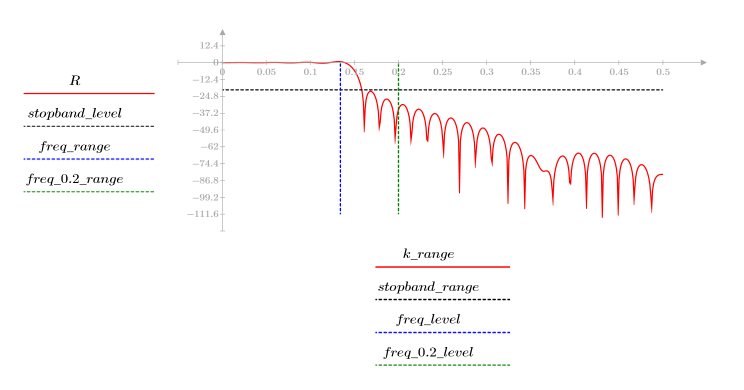
3. Utilizzare la funzione gain per calcolare il rendimento in dB di questo filtro, con coefficienti vg, a una frequenza di k/1000 e per tracciare il relativo grafico.
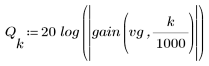
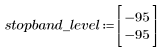
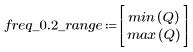
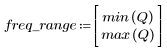
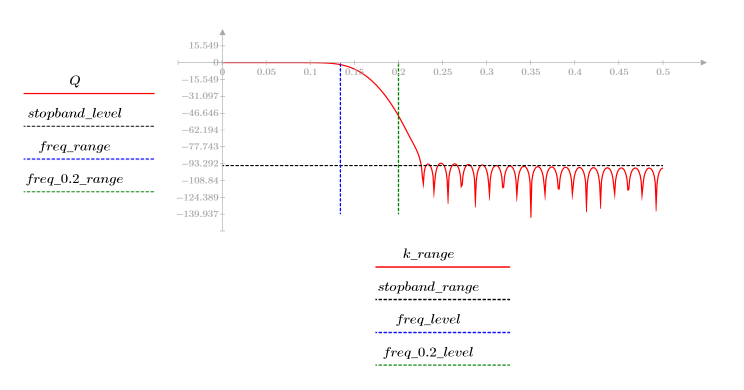
L'ondulazione della banda di reiezione è di circa -95 dB.
Finestra di Kaiser
La funzione kaiser restituisce la finestra di Kaiser con larghezza N e parametro b. Il parametro b deve soddisfare la condizione 2≤b≤20.
Il k-esimo elemento del vettore risultante è determinato dalla formula riportata di seguito.
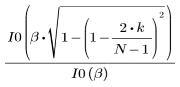
1. Applicare la funzione al filtro di ordine N e tracciare un grafico del vettore risultante.
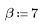
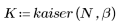
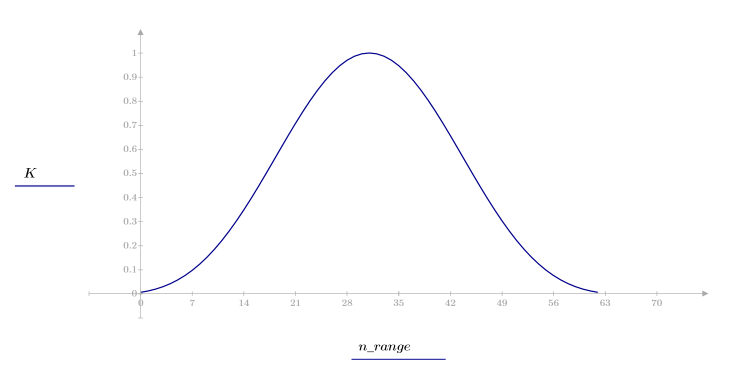
2. Calcolare la risposta all'impulso finestrato.
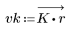
3. Utilizzare la funzione gain per calcolare il rendimento in dB di questo filtro, con coefficienti vk, a una frequenza di k/1000 e per tracciare il relativo grafico.
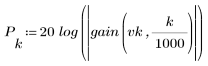
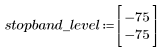
L'ondulazione della banda di reiezione è di circa -75 dB.
Finestra di Chebyshev
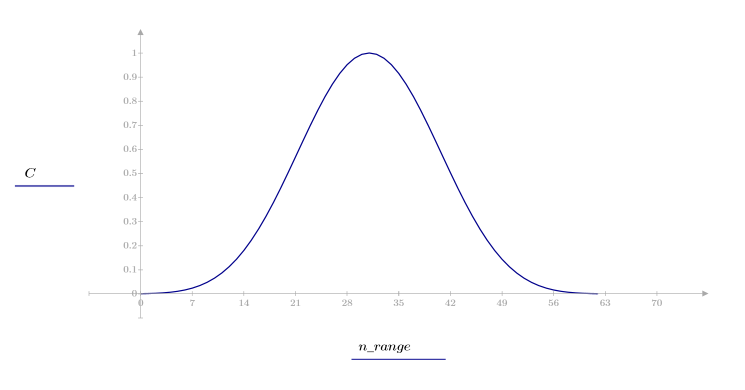
La funzione cheby restituisce la finestra di Chebyshev o con finestra equiripple di larghezza N e parametro b. Il parametro b specifica l'ondulazione massima del lobo laterale in dB e deve soddisfare la condizione 1 < b. In genere, b è > 50. La lunghezza di questa finestra deve essere dispari. La finestra di Chebyshev viene calcolata prendendo la trasformata di Fourier discreta inversa di un polinomio di Chebyshev valutata in corrispondenza dei punti intorno alla circonferenza di raggio unitario. Per ulteriori informazioni su questa finestra, vedere Programs for Digital Signal Processing (IEEE Press).
1. Applicare la funzione al filtro di ordine N e tracciare un grafico del vettore risultante.
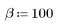
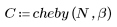
2. Calcolare la risposta all'impulso finestrato.
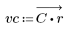
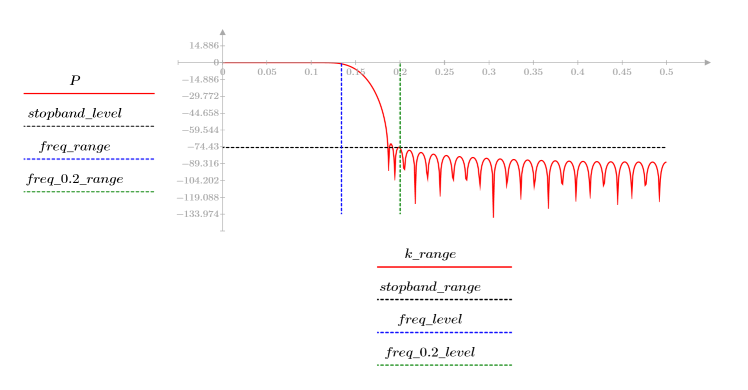
3. Utilizzare la funzione gain per calcolare il rendimento in dB di questo filtro, con coefficienti vc, a una frequenza di k/1000 e per tracciare il relativo grafico.
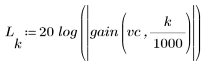
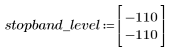
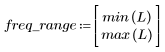
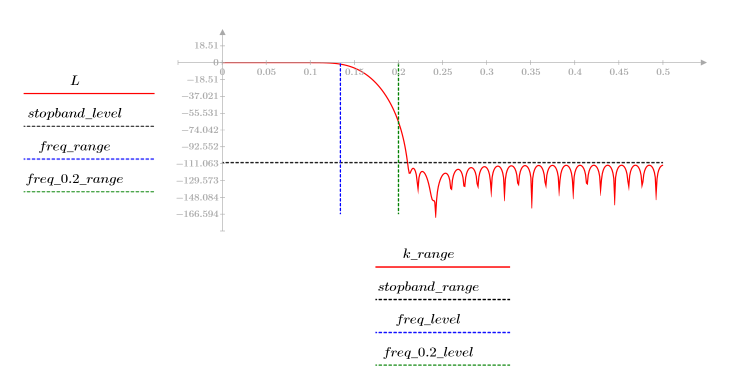
L'ondulazione della banda di reiezione è di circa -110 dB.
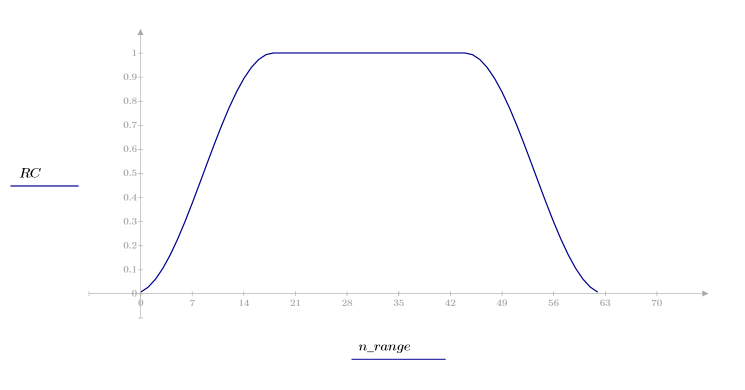
Finestra coseno rialzato
La funzione costaper è simile alla funzione taprect per il fatto che restituisce una finestra rettangolare con estremità assottigliate che seguono una curva di coseno. È tuttavia possibile utilizzare il parametro a per specificare la percentuale della finestra che deve essere creata con una curva di coseno. Il parametro a deve essere compreso tra 0 e 1. Un valore 0 restituisce una finestra rettangolare, mentre un valore 1 restituisce una curva di coseno rialzata.
Per la parte assottigliata della finestra, il valore del k-esimo elemento è dato da:
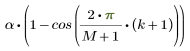
dove M è il numero di elementi della finestra che rientrano in una delle estremità e deriva da a-N:
1. Applicare la funzione al filtro di ordine N e tracciare un grafico del vettore risultante.
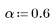
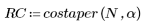
2. Calcolare la risposta all'impulso finestrato.
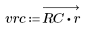
3. Utilizzare la funzione gain per calcolare il rendimento in dB di questo filtro, con coefficienti vrc, a una frequenza di k/1000 e per tracciare il relativo grafico.
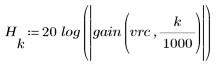
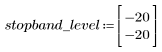
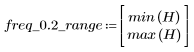
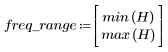
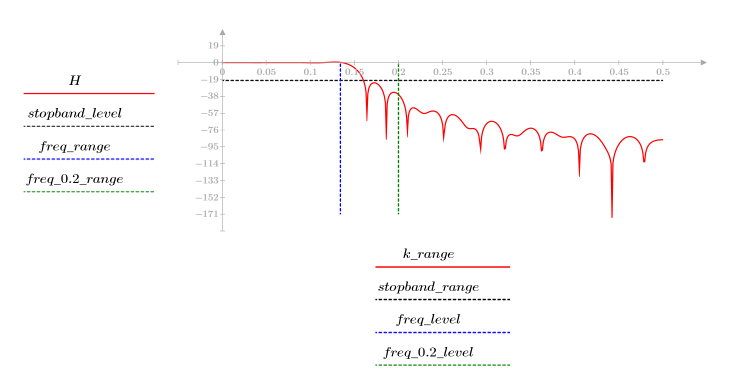
L'ondulazione della banda di reiezione è di circa -20 dB.
Riferimenti
• S. Lawrence Marple, Jr., Digital Spectral Analysis with Applications, Prentice-Hall (1987)
• Lawrence R. Rabiner and Bernard Gold, Theory and Application of Digital Signal Processing, Prentice-Hall, Inc. (1975).
• T. W. Parks and C. S. Burrus, Digital Filter Design, Wiley-Interscience (1987).