Esempio: grafici quantile-quantile

Funzioni > Statistica > Statistiche grafiche > Esempio: grafici quantile-quantile

Utilizzare la funzione qqplot per creare grafici quantile-quantile (Q-Q).

Due insiemi di dati

Confrontare i quantili di due insiemi di dati in un grafico Q-Q per verificare se hanno la stessa distribuzione.

1. Definire un insieme di dati.

Fare clic per copiare questa espressione

La colonna 2 mostra il batch in cui è stata effettuata la misurazione e la colonna 3 mostra la forza misurata delle barre di nitrato di silicio legato.

2. Estrarre le due colonne di interesse, 2 e 3.

<region id="ID0EL2DBB" top="345.6" left="38.400000000000006" height="25.6" width="377.50000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="156">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">BatchData</id>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">submatrix</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Data</id>
          <real>0</real>
          <apply>
            <minus />
            <apply>
              <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">rows</id>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Data</id>
            </apply>
            <real>1</real>
          </apply>
          <real>2</real>
          <real>3</real>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

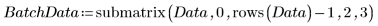
3. Chiamare vlookup per dividere i dati in base al fatto che le misurazioni siano state effettuate nel batch 1 o 2.

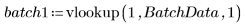
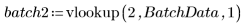
4. Calcolare il primo e il terzo quartile di ogni batch.

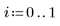
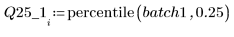
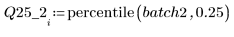
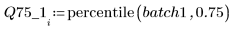
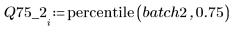
5. Tracciare un grafico Q-Q e un grafico dei quantili.

<region id="ID0EIEEBB" top="806.40000000000009" left="19.200000000000003" height="552" width="593.999999999999" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="178">
          <traceStyle color="#FF800080" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="179">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="180">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="181">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="182">
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="183">
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="474.799999999999" height="360" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="345" end="845">
          <axisLine position="bottom" positionticmark="-1" legendWidth="335.533333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="184">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">qq</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="185">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="186">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="187">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="188">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q25_2</id>
              </math>
              <math resultRef="189">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="190">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q75_2</id>
              </math>
              <math resultRef="191">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="192">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="193">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="345" end="845">
          <axisLine position="left" positionticmark="-1" legendWidth="95.5333333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="194">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">qq</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="195">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="196">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="197">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="198">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="199">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="200">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="201">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="202">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q25_1</id>
              </math>
              <math resultRef="203">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="204">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q75_1</id>
              </math>
              <math resultRef="205">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

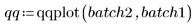
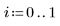
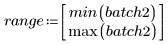
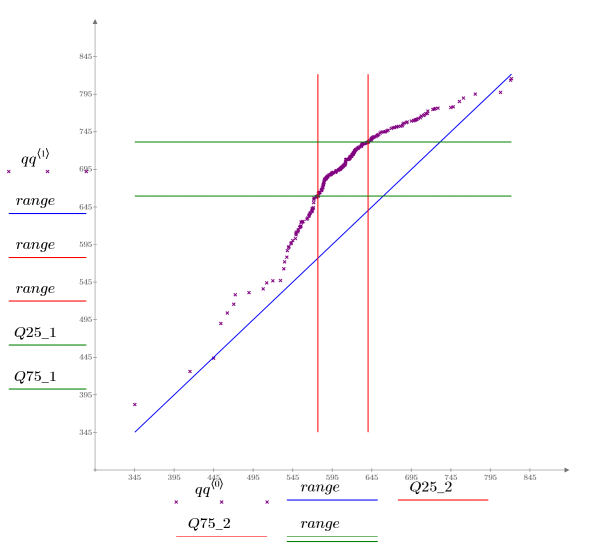
Viene tracciata una linea di riferimento 1 a 1, per enfatizzare la variazione dei dati.

Il grafico Q-Q mostra che i due batch non condividono la stessa distribuzione, sebbene i valori per percentili molto piccoli e molto grandi siano simili. I quantili del batch 1 sono significativamente più alti di quelli del batch 2 e questo suggerisce condizioni di elaborazione molto diverse.

Distribuzione normale

Determinare se le misurazioni da un misuratore di flusso di calore sono state ottenute in modo casuale. Verificare se le misurazioni sono distribuite normalmente, confrontandole con la distribuzione normale in un grafico Q-Q.

1. Definire un insieme di dati per il flusso di calore.

2. Trovare i punti dati per il grafico Q-Q normale.

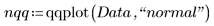
3. Trovare la linea di best fit per visualizzare la vicinanza dei quantili dei dati ai quantili della distribuzione normale.

<region id="ID0EDKEBB" top="2016.0000000000002" left="38.400000000000006" height="25.6" width="152.6866666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="234">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">BestFit</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <plus />
        <apply>
          <mult />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
        </apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">b</id>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

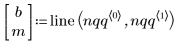
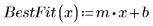
4. Tracciare un grafico quantile-quantile con la linea di best fit.

<region id="ID0EULEBB" top="2092.8" left="19.200000000000003" height="312" width="590.999999999999" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="236">
          <traceStyle color="#FFFF0000" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="237">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="394.999999999999" height="235.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="9.15" end="9.4">
          <axisLine position="origin" positionticmark="5" legendWidth="91.2633333333333" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="244">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">nqq</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="245">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="239">
              <real xmlns="http://schemas.mathsoft.com/math50">9.15</real>
            </startValue>
            <secondTickValue resultRef="241">
              <real xmlns="http://schemas.mathsoft.com/math50">9.20</real>
            </secondTickValue>
            <endValue resultRef="243">
              <real xmlns="http://schemas.mathsoft.com/math50">9.35</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-3.5" end="3.5">
          <axisLine position="left" positionticmark="-1" legendWidth="157.56" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="246">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">nqq</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="247">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="248">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">BestFit</id>
                  <apply>
                    <matcol />
                    <id xml:space="preserve">nqq</id>
                    <real>0</real>
                  </apply>
                </apply>
              </math>
              <math resultRef="249">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

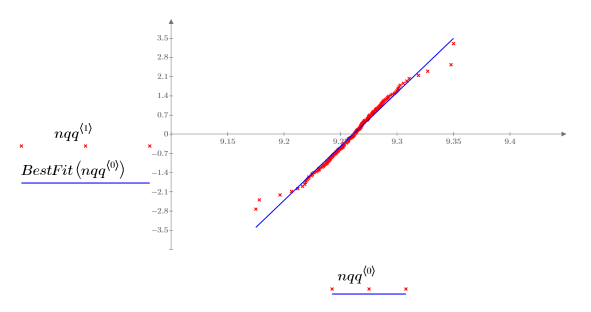
La correlazione molto stretta con la linea di riferimento indica che i campioni sono distribuiti normalmente.

Il controllo della normalità è uno dei test eseguiti durante il rilevamento degli outlier.

Distribuzione di Weibull

Verificare se un insieme di dati segue una distribuzione di Weibull.

1. Registrare nel vettore R la tensione per la quale l'isolamento elettrico risulta insufficiente per cavi soggetti a sollecitazione di tensione in aumento.

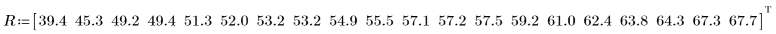
2. Tracciare un istogramma dei dati.

<region id="ID0EAREBB" top="2880.0000000000005" left="19.200000000000003" height="312" width="589.906666755675" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="267">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <graph-size width="470.706666755675" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="32.5" end="72.5">
          <axisLine position="origin" positionticmark="0" legendWidth="115.576666666667" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="270">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <plus />
                  <id xml:space="preserve">bins</id>
                  <real>2.5</real>
                </apply>
              </math>
              <math resultRef="271">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="269">
              <real xmlns="http://schemas.mathsoft.com/math50">37.5</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="5">
          <axisLine position="left" positionticmark="-1" legendWidth="85.6133333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="272">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">stem</id>
              </math>
              <math resultRef="273">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

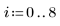
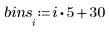
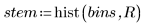
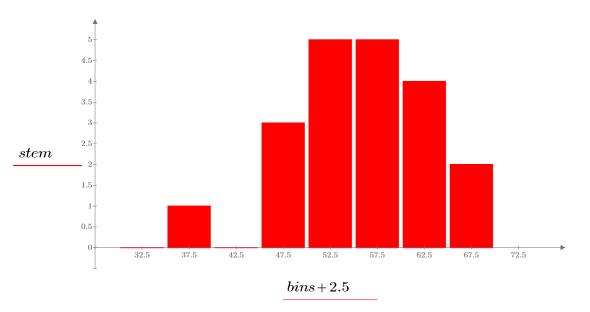
L'istogramma mostra che i dati non hanno una distribuzione normale. Vi è una dissimmetria dei dati che sono spostati da un lato. È possibile confrontare i dati con una distribuzione di Weibull in un grafico Q-Q.

3. Trovare i punti dati per il grafico Q-Q di Weibull.

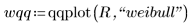
4. Trovare la linea di best fit per visualizzare la vicinanza dei quantili dei dati ai quantili della distribuzione di Weibull.

<region id="ID0EVUEBB" top="3494.4000000000005" left="38.400000000000006" height="25.6" width="152.6866666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="283">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">BestFit</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <plus />
        <apply>
          <mult />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
        </apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">b</id>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

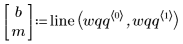
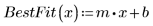
5. Tracciare un grafico quantile-quantile con la linea di best fit.

<region id="ID0EGWEBB" top="3571.2000000000007" left="19.200000000000003" height="312" width="592.999999999999" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="285">
          <traceStyle color="#FFFF0000" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="286">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="396.999999999999" height="235.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="3.6" end="4.3">
          <axisLine position="origin" positionticmark="8" legendWidth="93.3466666666667" />
          <axisGrid>
            <gridFrequency>8</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="293">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">wqq</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="294">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="288">
              <real xmlns="http://schemas.mathsoft.com/math50">3.60</real>
            </startValue>
            <secondTickValue resultRef="290">
              <real xmlns="http://schemas.mathsoft.com/math50">3.7</real>
            </secondTickValue>
            <endValue resultRef="292">
              <real xmlns="http://schemas.mathsoft.com/math50">4.3</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-6.4" end="2.4">
          <axisLine position="left" positionticmark="-1" legendWidth="159.643333333333" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="295">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">wqq</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="296">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="297">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">BestFit</id>
                  <apply>
                    <matcol />
                    <id xml:space="preserve">wqq</id>
                    <real>0</real>
                  </apply>
                </apply>
              </math>
              <math resultRef="298">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

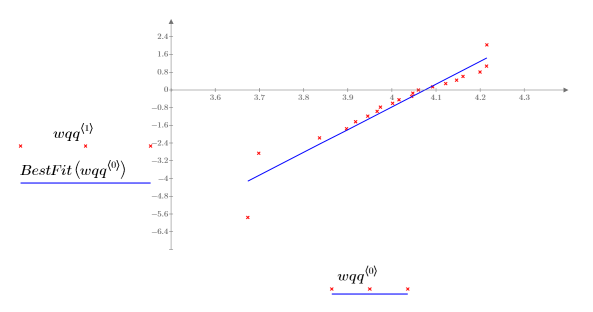
La stretta correlazione con la linea di riferimento indica che l'insieme di dati può essere modellato da una distribuzione di Weibull.

Per i grafici Q-Q di Weibull, viene utilizzata una scala logaritmica.

Riferimenti

Lawless, J.F., Statistical Methods for Lifetime Data, second ed, Wiley-Interscience, 2002.

Argomenti correlati

Grafico quantile-quantile

È stato utile?