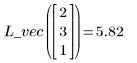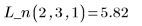Esempio: adattamento quadratico a pezzi

Funzioni > Analisi dati > Curve fitting > Esempio: adattamento quadratico a pezzi

Regressione polinomiale monovariabile

Utilizzare la funzione loess per adattare una serie di funzioni quadratiche ai dati utilizzando la regressione locale.

1. Definire la matrice riportata di seguito:

Fare clic per copiare questa espressione

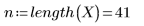
2. Definire l'estensione, la percentuale del numero totale di punti in una finestra ponderata attorno a ogni punto dati, utilizzata per adattamenti quadratici successivi dalla funzione loess.

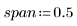
Le linee guida generali prevedono che (span*n) sia >1, in quanto si desidera che venga calcolata la media del numero di punti maggiore di 1 in ogni fit ponderato ai minimi quadrati:

3. Chiamare le funzioni loess e interp per eseguire l'adattamento quadratico a pezzi.

<region id="ID0EF55S" top="1382.4" left="19.2" width="243.793333333333" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="58">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="None" xml:space="preserve">fitloess</id>
        <boundVars>
          <id label="None" xml:space="preserve">t</id>
        </boundVars>
      </function>
      <apply>
        <id label="Function" xml:space="preserve" label-is-contextual="true">interp</id>
        <sequence>
          <id label="Variable" xml:space="preserve" label-is-contextual="true">cloess</id>
          <id label="Variable" xml:space="preserve" label-is-contextual="true">X</id>
          <id label="Variable" xml:space="preserve" label-is-contextual="true">Y</id>
          <id label="Variable" xml:space="preserve" label-is-contextual="true">t</id>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

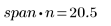
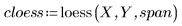
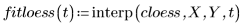
4. Chiamare la funzione polyfit per adattare un polinomio di secondo ordine all'insieme di dati.

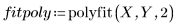
5. Tracciare il grafico delle due curve definite in precedenza.

<region id="ID0EIE6S" top="1900.8" left="0" width="619" height="288" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="false" background-type="white" show-axis-expressions="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="66">
          <traceStyle color="#FFFF0000" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="67">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
        <trace resultRef="68">
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="484.6" height="192" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-10" end="30">
          <axisLine position="ticknumberlock" positionticmark="1" legendWidth="215.593333333333" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="69">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">X</id>
              </math>
              <math resultRef="70">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="71">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">k_range</id>
              </math>
              <math resultRef="72">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-10" end="110">
          <axisLine position="ticknumberlock" positionticmark="0" legendWidth="105.443333333333" />
          <axisGrid>
            <gridFrequency>13</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="73">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Y</id>
              </math>
              <math resultRef="74">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="75">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">FTloess</id>
              </math>
              <math resultRef="76">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="77">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">FTpoly</id>
              </math>
              <math resultRef="78">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

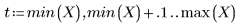
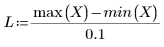
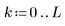
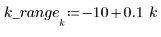
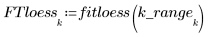
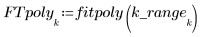
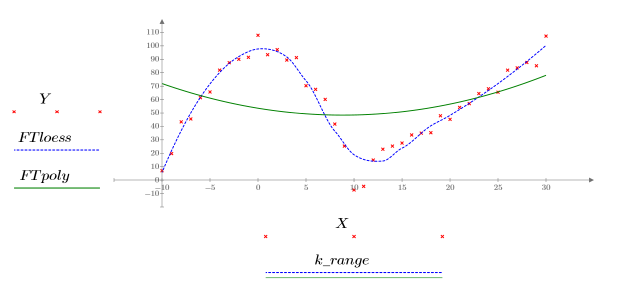
• Quando l'estensione è ampia (ad esempio 2 o 3), i dati vengono considerati un singolo fit quadratico con pesi quasi uguali. Il fit si avvicina la soluzione di polyfit a un polinomio quadratico.

• Non vi sono linee guida esatte per la scelta dell'estensione. Con l'aumentare dell'estensione, il grafico del fit di loess diventa più uniforme, poiché nel fit viene connesso un numero minore di pezzi. Il fit potrebbe tuttavia non seguire correttamente le caratteristiche dei dati. Al contrario, con il diminuire dell'estensione, potrebbe risultare che loess non converge.

• L'algoritmo loess non è progettato per l'estrapolazione. Se si tenta di valutare interp in corrispondenza di valori al di là dell'intervallo x originale, viene restituito un errore.

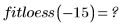
• Potrebbe essere consigliabile utilizzare loess quando i dati hanno una caratteristica piuttosto discontinua, ma quando non si desidera eseguire il fit a pezzi manuale o utilizzare metodi di adattamento complessi, non realistici dal punto di vista fisico o non lineari.

Regressione polinomiale multivariata

Utilizzare la funzione loess per eseguire la regressione polinomiale multivariata. La funzione loess non consente di adattare più di 4 variabili indipendenti.

1. Definire un insieme di dati.

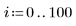
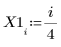
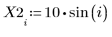
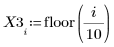
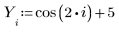
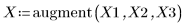
2. Definire un parametro di smoothing.

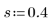
Questo parametro ha lo stesso significato dello studio a un fattore.

3. Chiamare la funzione loess.

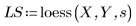
4. Chiamare interp per interpolare le funzioni di adattamento multivariate. La funzione adattata può accettare un vettore di n elementi o un insieme di n argomenti, dove n è il numero di fattori indipendenti.

<region id="ID0EST6S" top="3225.6" left="38.4" width="217.316666666667" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="98">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="None" xml:space="preserve">L_vec</id>
        <boundVars>
          <id label="None" xml:space="preserve">v</id>
        </boundVars>
      </function>
      <apply>
        <id label="Function" xml:space="preserve" label-is-contextual="true">interp</id>
        <sequence>
          <id label="Variable" xml:space="preserve" label-is-contextual="true">LS</id>
          <id label="Variable" xml:space="preserve" label-is-contextual="true">X</id>
          <id label="Variable" xml:space="preserve" label-is-contextual="true">Y</id>
          <id label="Variable" xml:space="preserve" label-is-contextual="true">v</id>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EAU6S" top="3283.2" left="38.4" width="285.353333333333" height="62.8" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="99">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="None" xml:space="preserve">L_n</id>
        <boundVars>
          <id label="None" xml:space="preserve">x1</id>
          <id label="None" xml:space="preserve">x2</id>
          <id label="None" xml:space="preserve">x3</id>
        </boundVars>
      </function>
      <apply>
        <id label="Function" xml:space="preserve" label-is-contextual="true">interp</id>
        <sequence>
          <id label="Variable" xml:space="preserve" label-is-contextual="true">LS</id>
          <id label="Variable" xml:space="preserve" label-is-contextual="true">X</id>
          <id label="Variable" xml:space="preserve" label-is-contextual="true">Y</id>
          <matrix rows="3" cols="1">
            <id label="Variable" xml:space="preserve" label-is-contextual="true">x1</id>
            <id label="Variable" xml:space="preserve" label-is-contextual="true">x2</id>
            <id label="Variable" xml:space="preserve" label-is-contextual="true">x3</id>
          </matrix>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

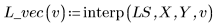
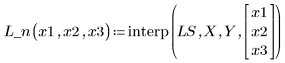
5. Utilizzare le funzioni di adattamento per predire il valore di Y in corrispondenza del punto (2, 3, 1).

Argomenti correlati

Regressione polinomiale localizzata

È stato utile?