Esempio: simulazione Monte Carlo
Utilizzare la funzione montecarlo per generare campioni casuali per simulare una funzione.
1. Definire una funzione da simulare.
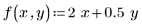
2. Definire la distribuzione di ogni parametro.
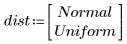
3. Definire la deviazione media e la deviazione standard di ogni distribuzione. Registrare i risultati nella matrice Rvals.
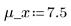 | 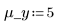 |
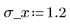 | 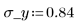 |
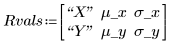
4. Impostare un limite superiore per il parametro Y.
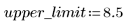
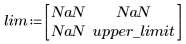
5. Definire il numero di campioni da generare.
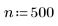
6. Chiamare montecarlo per generare i campioni.
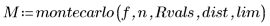
L'output restituito dalla funzione montecarlo è una matrice di tre colonne.
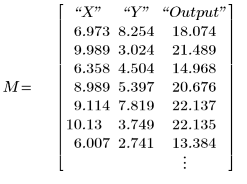
Le prime due colonne sono i campioni generati per ogni parametro. L'ultima colonna è l'output della funzione f per questi parametri.
7. Registrare i valori generati in vettori distinti.
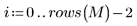 | 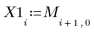 |
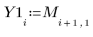 | 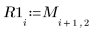 |
È possibile verificare che l'ultimo vettore R1 sia effettivamente il risultato della funzione f:
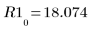
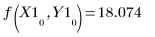
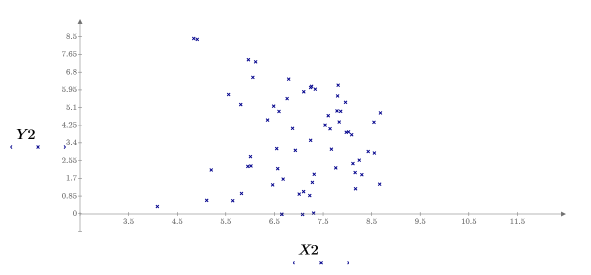
8. Tracciare il grafico dei parametri mettendoli a confronto e tracciare il grafico della loro media.
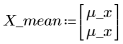 | 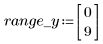 |
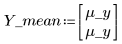 | 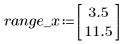 |
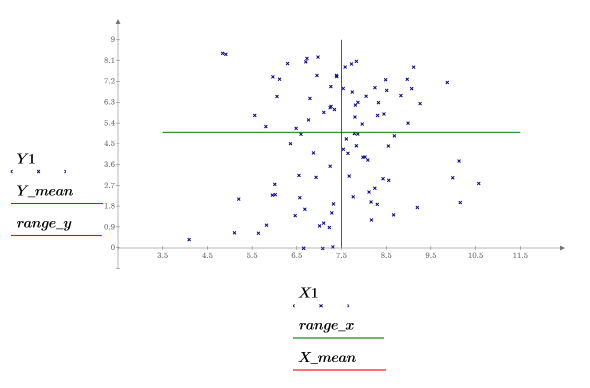
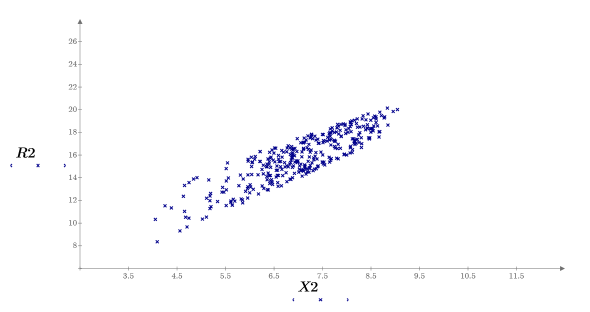
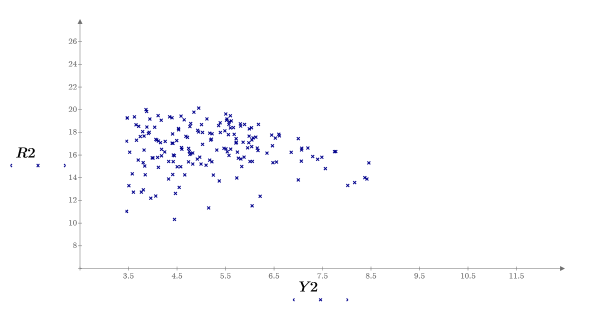
I campioni sono distribuiti uniformemente lungo l'asse y e distribuiti normalmente lungo l'asse x. I campioni con un valore y maggiore di 8,5 sono stati eliminati.
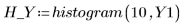
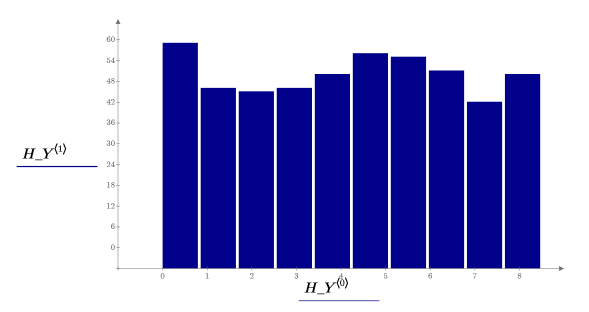
I valori y sono distribuiti uniformemente. I campioni sono generati entro 6 deviazioni standard su ogni lato della media:
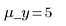
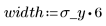
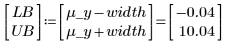
Se i campioni generati sono maggiori del limite superiore, vengono eliminati:
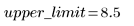
10. Chiamare histogram per separare i valori x in 10 barre. Tracciare un istogramma dei valori y e aggiungere una distribuzione normale.
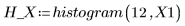
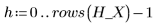
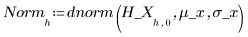
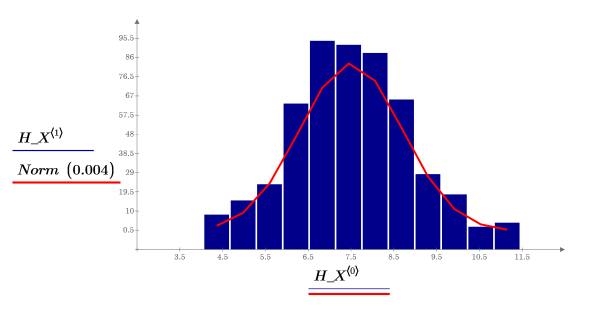
I valori x sono distribuiti normalmente.
11. Tracciare un grafico dei risultati calcolati in funzione dei singoli parametri.
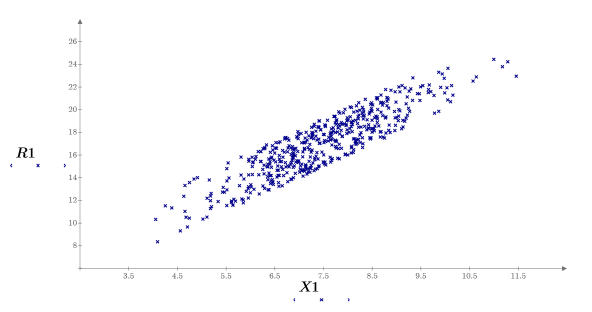
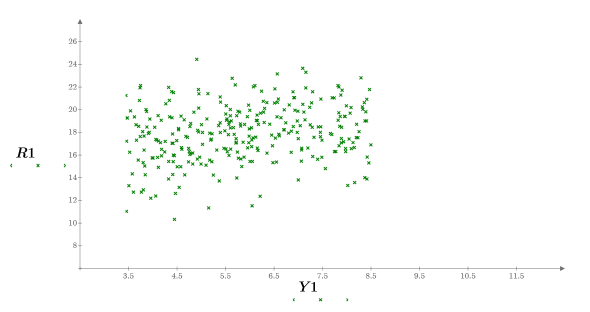
12. Chiamare il costrutto speciale if per definire i vincoli e per sostituire i risultati con NaN quando non rientrano nei vincoli.
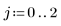
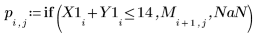
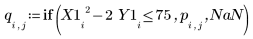
13. Tracciare il grafico dei parametri mettendoli a confronto.
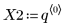
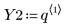
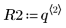
14. Tracciare un grafico dei risultati calcolati in funzione dei singoli parametri.