Esempio: trasformata coseno discreta

Funzioni > Elaborazione immagini > Dominio della trasformata > Esempio: trasformata coseno discreta

Utilizzare le funzioni dct e idct per calcolare rispettivamente la trasformata coseno discreta e la trasformata inversa. Questa trasformata offre il vantaggio di concentrare la maggior parte dell'"energia" dell'immagine, ovvero le informazioni, in pochi componenti di frequenza, costituendo una scelta efficace per la codifica.

Per informazioni sull'utilizzo di questo esempio, fare riferimento a Esempi di elaborazione delle immagini.

1. Definire una matrice M con dimensioni N x P.

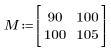
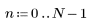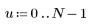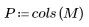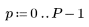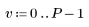2. L'implementazione della trasformata coseno utilizza la trasformata coseno discreta di tipo II. Definire DCT come formula analitica per la trasformata.

Fare clic per copiare questa espressione

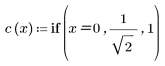
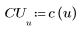
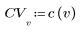
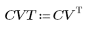
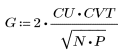
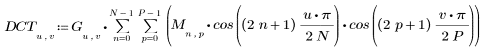
3. Valutare la matrice DCT.

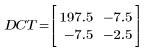
4. Applicare la funzione dct alla matrice M.

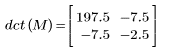
5. Calcolare l'errore massimo tra DCT e la funzione dct.

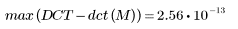
Compattazione dell'energia

La trasformata coseno ha proprietà di compattazione dell'energia molto efficaci, ovvero concentra la maggior parte dell'energia nei primi coefficienti della trasformata.

1. Definire una matrice di input.

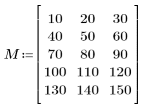
2. Applicare la funzione dct alla matrice M e valutarla.

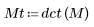
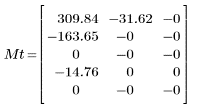
La matrice risultante mostra che la maggior parte dell'energia, correlata ai valori di coefficiente, è concentrata nei primi elementi.

idct

La funzione inversa consente di recuperare un'immagine originale dalla relativa trasformata.

1. Leggere una versione in bianco e nero della Monna Lisa.

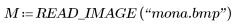
(mona.bmp)

2. Applicare la funzione dct per trasformare l'immagine.

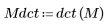
(mona_noise.bmp)

3. Applicare la funzione inversa per recuperare l'immagine.

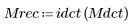
(mona_rec.bmp)

4. Verificare la proprietà di compattazione dell'energia della trasformata coseno discreta osservando gli istogrammi delle immagini trasformata e originale.

<region id="ID0EH6HZ" top="3000" left="24" width="597" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">k_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">H</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">Horig</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

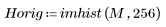
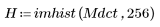
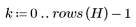
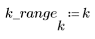
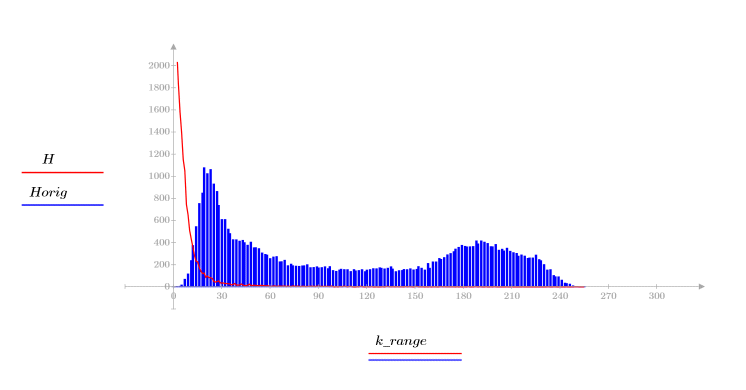
L'immagine trasformata concentra la maggior parte dell'energia nelle prime barre dell'istogramma, mentre la distribuzione dell'immagine originale è più estesa. Ciò rende l'immagine trasformata un candidato migliore per la codifica o la trasmissione, in quanto la maggior parte delle informazioni sull'immagine può essere trasmessa con un numero minimo di componenti di frequenza. Per questo motivo, la trasformata coseno discreta viene utilizzata per la compressione delle immagini.

Argomenti correlati

Trasformata coseno discreta

Istogrammi 1D e 2D

È stato utile?