Esempio: interpolazione di spline cubica
Utilizzare le funzioni lspline, pspline e cspline per costruire spline cubiche (polinomi a pezzi) e per eseguire l'interpolazione tra punti dati.
1. Definire una matrice.
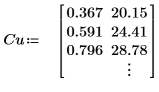
2. Utilizzare la funzione csort per ordinare i dati in modo che la seconda colonna di Cu sia in ordine crescente.
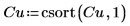
I valori x inseriti nelle funzioni spline devono essere in ordine crescente. |
3. Creare vettori contenenti i dati x e y.
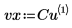
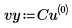
4. Utilizzare la funzione cspline per creare un vettore di spline cubica, quindi utilizzare la funzione interp per ottenere i valori interpolati.
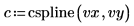
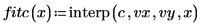
5. Utilizzare la funzione lspline per creare un vettore di spline lineare, quindi utilizzare la funzione interp per ottenere i valori interpolati.
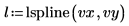
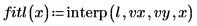
6. Utilizzare la funzione pspline per creare un vettore di spline parabolica, quindi utilizzare la funzione interp per ottenere i valori interpolati.
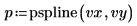
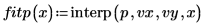
7. Tracciare il grafico dei punti dati originali e delle spline cubiche.
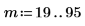
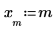
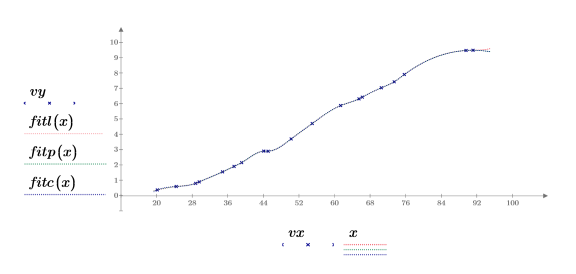
8. Eseguire lo zoom avanti dei primi due punti dati.
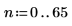
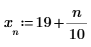
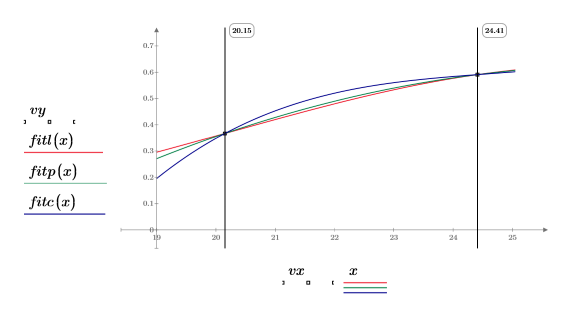
Le tre funzioni spline producono risultati equivalenti, eccetto che nei punti finali.
9. Calcolare la derivata seconda del vettore di spline lineare interpolato e mostrare che è uguale a 0 in corrispondenza dei punti finali.
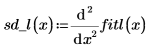 | |
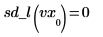 | 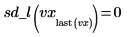 |
10. Calcolare la derivata seconda della spline parabolica interpolata e mostrare che in corrispondenza dei punti finali è uguale al valore del prossimo punto più vicino.
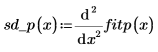
◦ Valutare la derivata seconda in corrispondenza del primo e del secondo punto e mostrare che sono uguali.
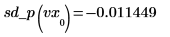
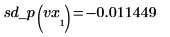
◦ Valutare la derivata seconda in corrispondenza dei punti dal secondo all'ultimo e dell'ultimo punto e mostrare che sono uguali.
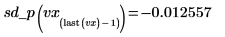
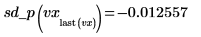
È possibile utilizzare le derivate dei fit delle spline per trovare i massimi e i minimi, il coefficiente angolare e altre caratteristiche delle curve interpolate.