Regresión no lineal
• genfit(vx, vy, vg, F): Devuelve un vector que contiene los parámetros que hacen que una función F de x y n parámetros u1... un se aproximen más a los datos en vx y vy.
La función genfit utiliza una versión optimizada del método de Levenberg-Marquardt para la minimización. Aunque con frecuencia es más rápida y menos sensible a los valores de prueba poco satisfactorios, esta implementación puede no converger bien en los problemas con muchos mínimos locales, tales como las funciones racionales. Esta implementación es sensible a los vectores de derivada incorrectos.
Argumentos
• vx, vy son vectores de valores de datos reales con la misma longitud que corresponden a los valores x y y en el conjunto de datos. Debe haber al menos tantos puntos de datos como parámetros.
• vg es un vector del elemento n de valores de prueba para los parámetros. Si n = 1, vg es escalar.
• F(x, u) es una función de ajuste o un vector de funciones, donde x es la variable independiente y u es un vector de parámetros o nombres de parámetros individuales. La siguiente ecuación es una representación válida de una función de ajuste:
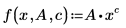
• n es un número entero positivo. En el caso de los parámetros no vectorizados, hay un límite de nueve nombres individuales.
Mejora de la convergencia
Para mejorar la convergencia y, posiblemente, la precisión de genfit, F se puede representar como un vector de funciones n+1 en el que la primera entrada F0 es la función de ajuste f y las demás entradas F1, F2,..., Fn son las derivadas parciales simbólicas de f con respecto a los parámetros n.
En relación a las dos maneras de representar la función de ajuste mostrada anteriormente, f(x,A,c) solo se puede utilizar si las derivadas parciales se buscan de forma simbólica. Por lo tanto, en la representación de F como un vector de funciones, n tiene un límite de 9, por lo que F tiene una longitud máxima de 10. El vector F se puede crear construyendo una matriz de las derivadas parciales adecuadas y evaluándola de forma simbólica:
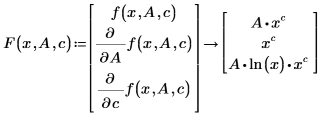
Información adicional
• Indique solo el nombre de la función de ajuste o el vector de funciones, sin argumentos, para genfit.
• Si se utiliza la función de ajuste sin las derivadas parciales de parámetro simbólicas, genfit calcula las derivadas parciales de parámetro de forma numérica. Es menos preciso que proporcionar las derivadas simbólicas, pero podría ser conveniente en algunos casos.
• Si genfit no se convierte, se puede intentar con otros valores de prueba o aplicando una escala a los datos para que todos los parámetros tengan un orden de magnitud similar. Igual que en todas las técnicas de resolución numérica, los problemas no lineales son muy sensibles a los valores de prueba.
• Se podría trazar la función de ajuste con los valores de prueba para refinarlos antes de utilizar genfit.
• El método de Levenberg-Marquardt optimizado es más sensible a los errores en las derivadas algebraicas proporcionadas. Si genfit falla, se deben verificar las expresiones derivadas.