Integrales de seno y coseno
• Si(x): la función integral seno se define según se indica a continuación.
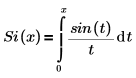
La representación de expansión en serie es:
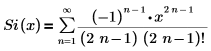
El resultado mostrado representa, tres de los seis valores por defecto, los términos de la serie que no tienen coeficientes de 0.
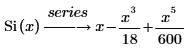
• Ci(x): la función integral del coseno se define como se indica a continuación.
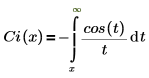
Otra forma de la definición es:
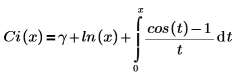
La representación de expansión en serie es:
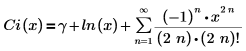
Los dos últimos términos representan, dos de los seis valores por defecto, los términos de la serie que no tienen coeficientes de 0.
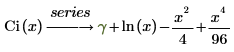
• Shi(x): la función integral seno hiperbólico se define según se indica a continuación.
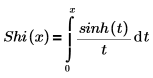
El resultado mostrado representa, tres de los seis valores por defecto, los términos de la serie que no tienen coeficientes de 0.
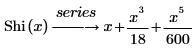
Los términos de la expansión en serie de las funciones Si y Shi son idénticos, a excepción del signo de los términos cuando n es un número par.
• Chi(x): la función integral del coseno hiperbólico se define como se indica a continuación.
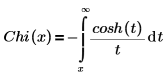
Otra forma de la definición es:
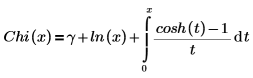
Los dos últimos términos representan, dos de los seis valores por defecto, los términos de la serie que no tienen coeficientes de 0.
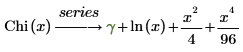
Los términos de la expansión en serie de las funciones Ci y Chi son idénticos, a excepción del signo de los términos cuando n es un número impar.
Argumentos
• x es un escalar real o complejo, o un vector de escalares reales o complejos.
Información adicional
Estas funciones resultan útiles con el uso de la palabra clave float, que evalúa de forma numérica las funciones en lugar de devolver expresiones matemáticas simbólicas.