Funciones gamma
• Γ(z): permite devolver el valor de la función gamma de Euler de z.
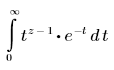
Las siguientes relaciones que implican a la función gamma pueden ser útiles:
◦ Γ(z + 1) = z · Γ(z)
◦ Γ(z)·Γ(1 − z) = π · csc(π · z)
◦ Γ(n + 1) = n!
• Γ(a, x): permite devolver el valor de la función gamma incompleta de x con el parámetro a. Γ(a, 0) = Γ(a).
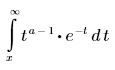
• lnΓ(z): permite devolver el logaritmo natural de la función gamma de Euler, evaluada en z.
Para escribir Γ, pulse G,Ctrl+G.
Utilice la función lnΓ para devolver resultados más pequeños y luego aplicar escala a ellos.
• Psi(y): permite devolver la derivada del logaritmo natural de la función Γ(y).
Argumentos
• z es un escalar complejo o real sin dimensiones, sin definir para z = 0, −1, −2...
Para Γ(z), solo se pueden evaluar los argumentos −107 ≤ Re(z) ≤ 171 y −106 ≤ Im(z) ≤ 106 sin sobrecarga numérica. Para z complejo, Γ(z) es la continuación analítica de la función real.
• a es un escalar real, positivo y sin dimensiones.
• x es un escalar real, positivo y sin dimensiones o 0.
• y es un número real.