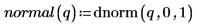Ejemplo: puntuación z de un vector de datos

Funciones > Estadísticas > Distribuciones de probabilidad > Ejemplo: puntuación z de un vector de datos

Calcule una puntuación z de un vector de datos distribuidos normalmente con desviación estándar de la población conocida.

1. Defina el conjunto de datos que desee analizar.

2. Calcule la media de la muestra m_s.

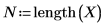
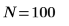
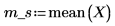
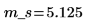
3. Defina el nivel de significancia, la desviación estándar de la población y la media de la población propuesta.

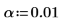
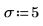
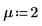
4. Calcule la puntuación z.

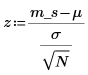
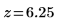
5. Declare la hipótesis nula y la alternativa para una prueba de dos colas.

H0: m = μ

H1: m ≠ μ

6. Utilice la función pnorm para calcular el valor p y probar la hipótesis. En este ejemplo, todas las expresiones booleanas se evalúan con 1 si la hipótesis nula es verdadera (no se rechaza H0).

<region id="ID0EF2YBB" top="883.20000000000016" left="38.400000000000006" height="25.6" width="185.36333333333334" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="84">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">P</id>
      <apply>
        <mult />
        <real>2</real>
        <parens>
          <apply>
            <minus />
            <real>1</real>
            <apply>
              <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">pnorm</id>
              <sequence>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">z</id>
                <real>0</real>
                <real>1</real>
              </sequence>
            </apply>
          </apply>
        </parens>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

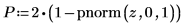
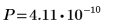
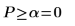
Existe una probabilidad de 4.11*10-10 de que la estadística de prueba sea mayor que la observada, suponiendo que la hipótesis nula sea verdadera. La comparación entre el valor p y el nivel de relevancia indica que hay pruebas de que la hipótesis alternativa es verdadera.

7. Utilice la función qnorm para calcular el límite de la región crítica y probar la hipótesis.

<region id="ID0ET5YBB" top="1171.2000000000003" left="38.400000000000006" height="47.2" width="163.91666666666669" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="90">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">crit</id>
      <apply>
        <absval />
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">qnorm</id>
          <sequence>
            <apply>
              <div />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">α</id>
              <real>2</real>
            </apply>
            <real>0</real>
            <real>1</real>
          </sequence>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

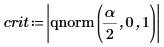
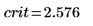
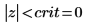
Rechace la hipótesis nula. Hay pruebas de que la media es distinta de μ.

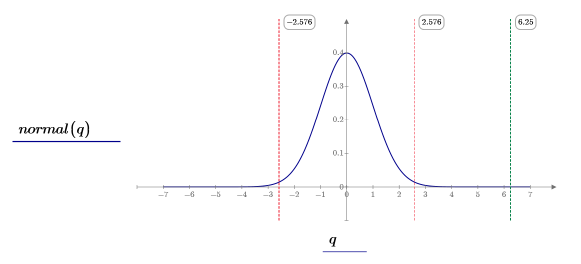
8. Utilice la función dnorm para calcular y trazar la distribución normal estándar (azul), los límites de la región crítica (rojo) y la puntuación z (verde).

<region id="ID0E4BZBB" top="1382.4" left="38.400000000000006" height="25.6" width="196.62333333333334" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="96">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="VARIABLE" xml:space="preserve">normal</id>
        <boundVars>
          <id labels="VARIABLE" xml:space="preserve">q</id>
        </boundVars>
      </function>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">dnorm</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">q</id>
          <real>0</real>
          <real>1</real>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Temas relacionados

Distribución normal

¿Fue esto útil?