Ejemplo: varianza y desviación estándar

Funciones > Estadísticas > Estadísticas descriptivas > Ejemplo: varianza y desviación estándar

Utilice las funciones Var y Stdev para comparar la dispersión de una distribución de Weibull y de una distribución normal.

1. Defina conjuntos de datos a continuación de una distribución de Weibull y una distribución normal.

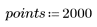
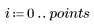
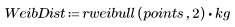
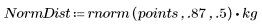
2. Trace las distribuciones.

<region id="ID0E2RUAB" top="312" left="0" width="626" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="0">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
        <trace resultRef="1">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id>NormHist</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <id label="Unit" xmlns="http://schemas.mathsoft.com/math50">kg</id>
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id>WeibHist</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <id label="Unit" xmlns="http://schemas.mathsoft.com/math50">kg</id>
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="2" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id>NormHist</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id>WeibHist</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

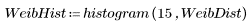
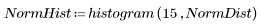
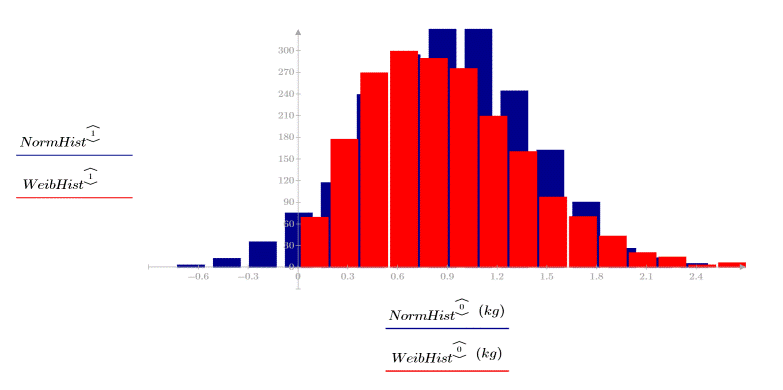
Los dos conjuntos de datos tienen distribuciones y formas distintas, aunque tengan medias parecidas:

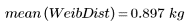
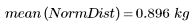
3. Calcule la varianza de la muestra de las distribuciones.

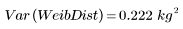
La menor varianza de la distribución de Weibull indica que está menos dispersa que la distribución normal.

La varianza de muestra se calcula del siguiente modo:

<region id="ID0EPVUAB" top="1080" left="24" width="394.69" height="67.2973333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="None">Variance</id>
        <boundVars>
          <id label="None">V</id>
        </boundVars>
      </function>
      <apply>
        <mult />
        <apply>
          <div />
          <real>1</real>
          <apply>
            <minus />
            <apply>
              <id>rows</id>
              <id>V</id>
            </apply>
            <real>1</real>
          </apply>
        </apply>
        <parens>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id>i</id>
              </boundVars>
              <apply>
                <pow />
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <indexer />
                      <id>V</id>
                      <id>i</id>
                    </apply>
                    <apply>
                      <id>mean</id>
                      <id>V</id>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <apply>
                  <id>rows</id>
                  <id>V</id>
                </apply>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </parens>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" />
    </resultFormat>
  </math>
</region>

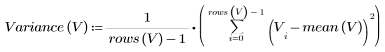
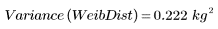
4. Calcule la desviación estándar de la muestra de la distribución de Weibull.

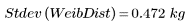
La desviación estándar tiene las mismas unidades que los datos originales, lo que la convierte en una medida ligeramente más intuitiva de la dispersión que la varianza. Se puede considerar una medida del error en una serie de medidas que deberían ser idénticas en realidad.

La desviación estándar de la muestra es la raíz cuadrada de la varianza de la muestra:

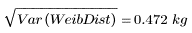
5. Calcule la varianza y las desviaciones estándar para la distribución de Weibull:

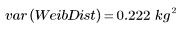
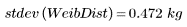
La varianza de la población y la desviación estándar se dividen entre el tamaño de la muestra, y no entre el tamaño de la muestra menos uno:

<region id="ID0ET1UAB" top="1584" left="24" width="369.073333333333" height="67.2973333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="None">variance</id>
        <boundVars>
          <id label="None">V</id>
        </boundVars>
      </function>
      <apply>
        <mult />
        <apply>
          <div />
          <real>1</real>
          <apply>
            <id>rows</id>
            <id>V</id>
          </apply>
        </apply>
        <parens>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id>i</id>
              </boundVars>
              <apply>
                <pow />
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <indexer />
                      <id>V</id>
                      <id>i</id>
                    </apply>
                    <apply>
                      <id>mean</id>
                      <id>V</id>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <apply>
                  <id>rows</id>
                  <id>V</id>
                </apply>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </parens>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" />
    </resultFormat>
  </math>
</region>

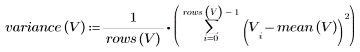
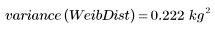
La varianza de la muestra, o función Var, es la definición usada con mayor frecuencia en el análisis de datos cuantitativo.

Temas relacionados

Varianza y desviación estándar

¿Fue esto útil?