Ejemplo: visualización de una ventana de señal
Utilice las funciones siguientes para realizar la visualización de una ventana de señal:
Respuesta en impulso de paso bajo ideal/truncada
1. Defina la respuesta en impulso h de un filtro de paso bajo ideal con una frecuencia de corte normalizada de 0.15.
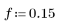
2. Defina la respuesta en impulso.
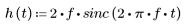
Un filtro de longitud finita y realizable debe tener una respuesta en impulso finita, por lo que esta respuesta ideal se trunca en un número manejable de términos.
3. Para verificar el efecto de la truncación directa sin crear ventanas de la respuesta en frecuencia, defina un filtro de longitud N que conste únicamente de N términos centrales de la respuesta ideal, desplazados para que el filtro resulte causal.
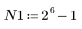
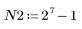
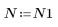
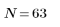
Como ejercicio, defina N en N2 y observe el efecto de aumentar el número de términos en los ejemplos siguientes.
4. Aplique la función de respuesta en impulso al rango de términos y trace la función resultante.
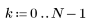
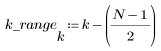
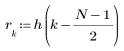
5. Calcule la respuesta en frecuencia para esta señal truncada con la función gain, pero defina primero el rango de frecuencias (múltiplos de la frecuencia de muestra).
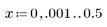
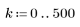
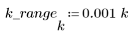
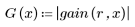
6. Recopile las magnitudes discretas de la función gain en un array nuevo.
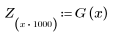
7. Busque la magnitud máxima de G y la frecuencia correspondiente.
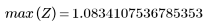
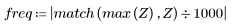
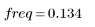
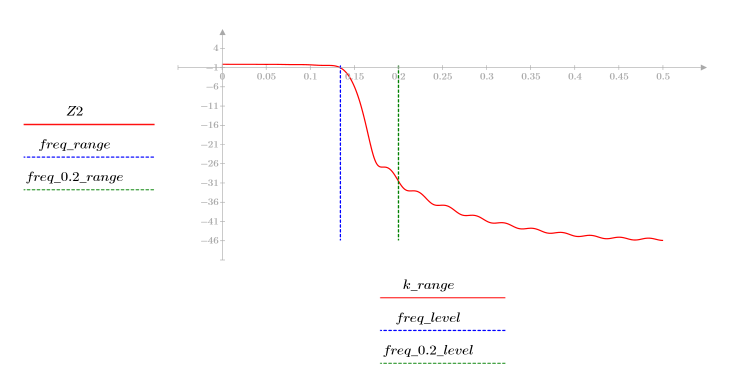
Cuando el número de términos sea igual a N1=63, la ganancia máxima de 1.083 se producirá a la frecuencia freq=0.134.
Cuando el número de términos sea igual a N2=127, la ganancia máxima de 1.092 se producirá a la frecuencia freq=0.142, por lo que estará más cerca del borde de la banda.
A una frecuencia freq=0.2, la ganancia disminuye hasta casi cero. Compare la ganancia alrededor de esta frecuencia en cada uno de los ejemplos siguientes.
8. Trace la función gain sobre el rango definido y muestre la frecuencia en que la magnitud presenta su valor máximo.
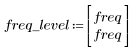
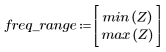
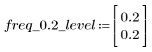
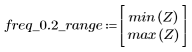
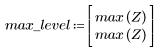
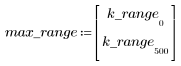
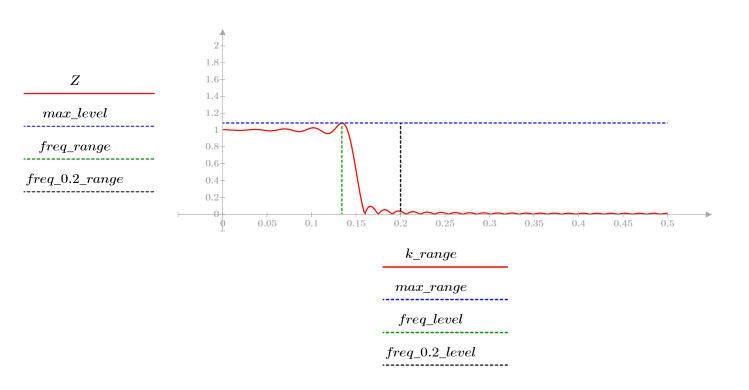
El rebase en el borde de la banda pasante se conoce como fenómeno de Gibbs. Si se aumenta el orden N del filtro de N1=63 a N2=127, el rebase se acercará al borde de banda, pero no reduce su amplitud.
La transición de 1 a 0 se hace más nítida con valores mayores del orden N del filtro.
Es posible producir una respuesta en frecuencia más deseable creando una ventana de la respuesta en impulso ideal, de modo que la transición a 0 en los bordes de la respuesta en impulso de filtro sea más suave. Las ventanas se multiplican término por término con un vector de respuesta r.
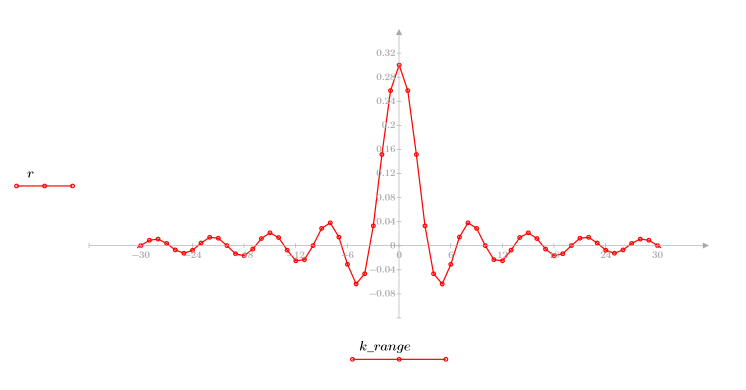
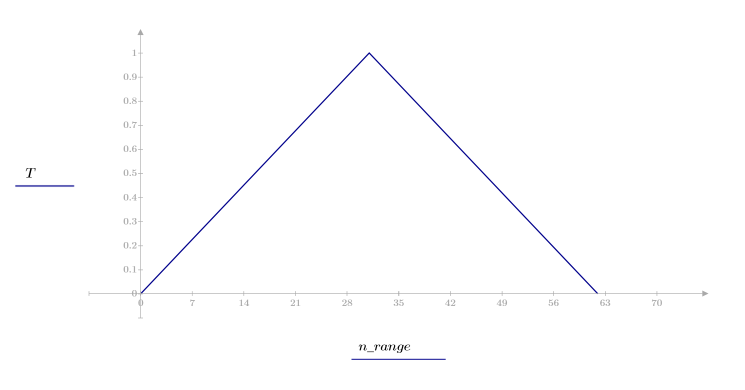
Ventana triangular
La función triangular devuelve la ventana de Bartlett o triangular de ancho N.
El elemento j del vector resultante viene dado por:
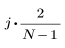
for
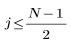
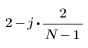
for
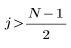
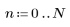
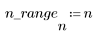
1. Aplique la función para filtrar por orden N y trazar el vector resultante.
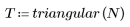
2. Calcule el impulso de respuesta en una ventana.
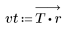
3. Utilice la función gain para calcular y trazar la ganancia en dB de este filtro, con coeficientes vt, a una frecuencia de k/1000.
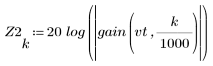
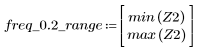
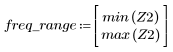
Ventana de Hanning
La función hanning devuelve la ventana de Hanning de ancho N.
El elemento k del vector resultante viene dado por:
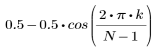
1. Aplique la función para filtrar por orden N y trazar el vector resultante.
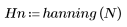
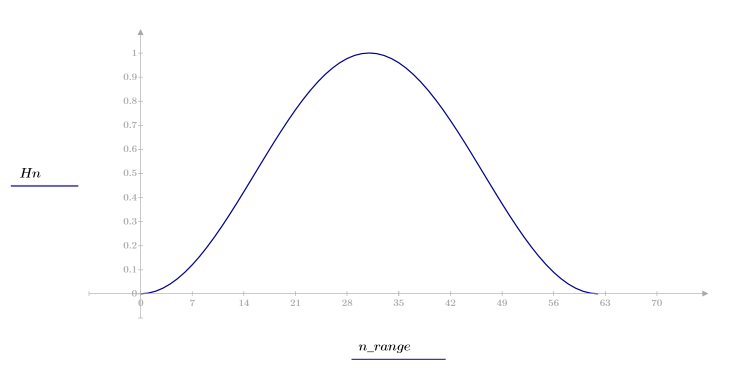
2. Calcule el impulso de respuesta en una ventana.
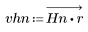
3. Utilice la función gain para calcular y trazar la ganancia en dB de este filtro, con coeficientes vhn, a una frecuencia de k/1000.
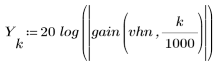
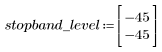
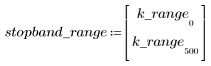
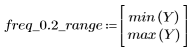
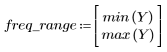
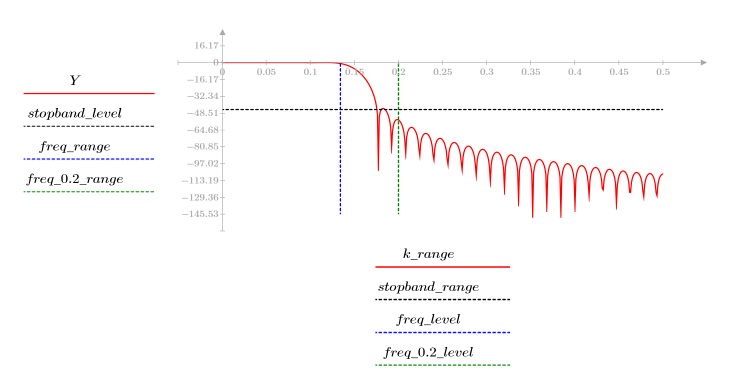
El rizado de la banda de supresión ronda los -45 dB.
Ventana de Hamming
La función hamming devuelve la ventana de Hamming de ancho N.
El elemento k del vector resultante viene dado por:
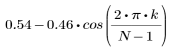
1. Aplique la función para filtrar por orden N y trazar el vector resultante.
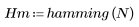
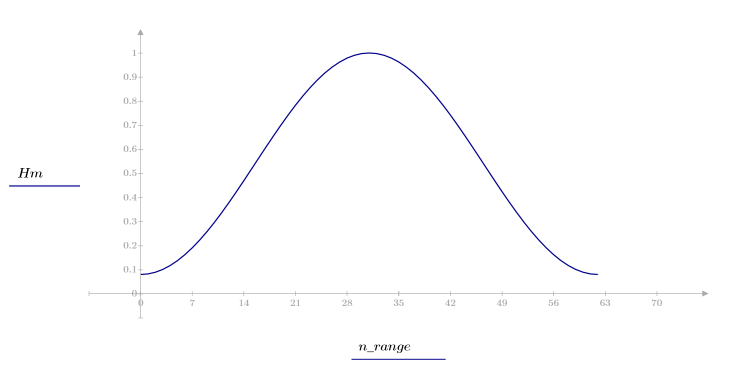
2. Calcule el impulso de respuesta en una ventana.
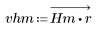
3. Utilice la función gain para calcular y trazar la ganancia en dB de este filtro, con coeficientes vhm, a una frecuencia de k/1000.
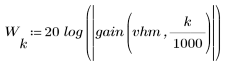
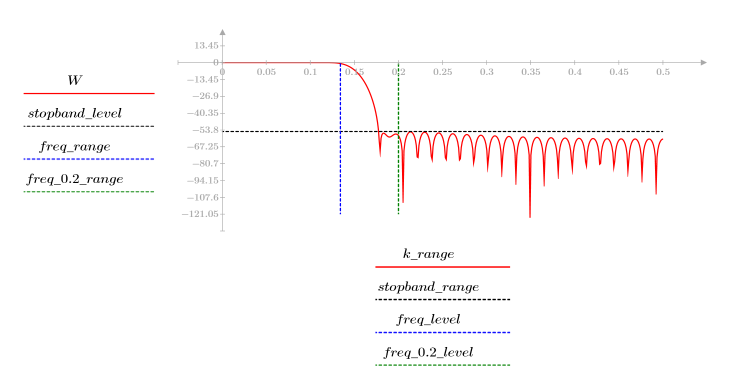
El rizado de la banda de supresión ronda los -55 dB.
Ventana de Blackman
La función blackman devuelve la ventana de Blackman de ancho N.
El elemento k del vector resultante viene dado por:
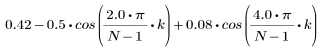
1. Aplique la función para filtrar por orden N y trazar el vector resultante.
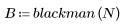
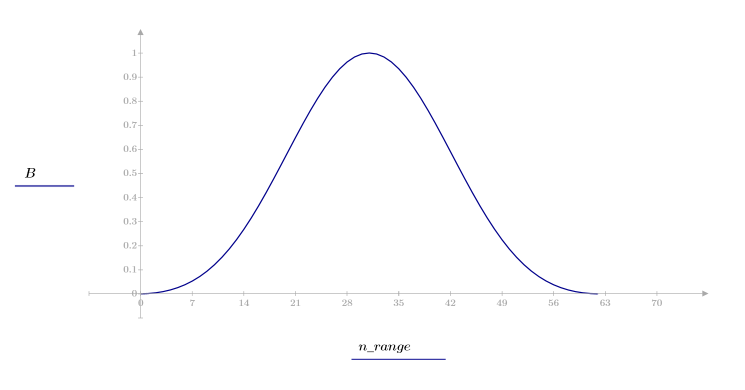
2. Calcule el impulso de respuesta en una ventana.
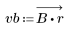
3. Utilice la función gain para calcular y trazar la ganancia en dB de este filtro, con coeficientes vb, a una frecuencia de k/1000.
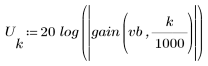
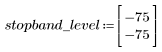
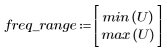
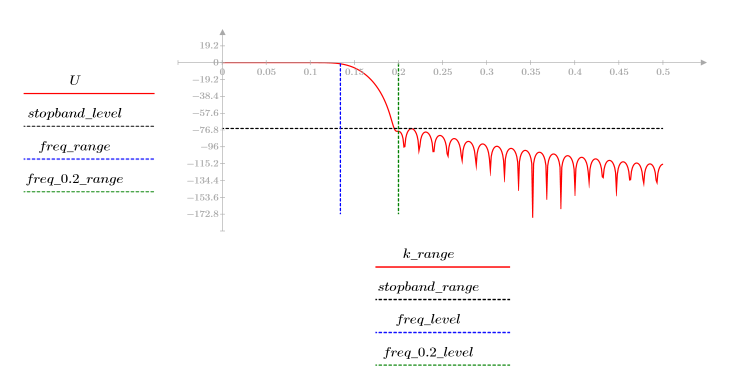
El rizado de la banda de supresión ronda los -75 dB.
Ventana de Nuttall
La función nuttall devuelve la ventana de Nuttall de ancho N.
El elemento k del vector resultante viene dado por:
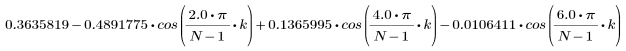
1. Aplique la función para filtrar por orden N y trazar el vector resultante.
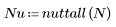
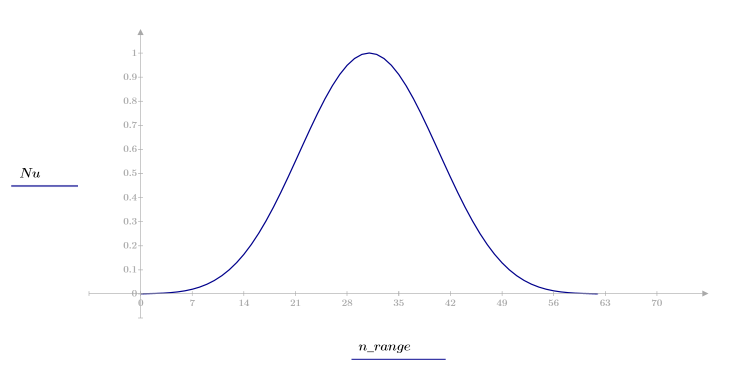
2. Calcule el impulso de respuesta en una ventana.
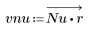
3. Utilice la función gain para calcular y trazar la ganancia en dB de este filtro, con coeficientes vnu, a una frecuencia de k/1000.
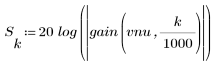
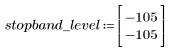
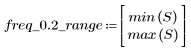
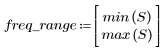
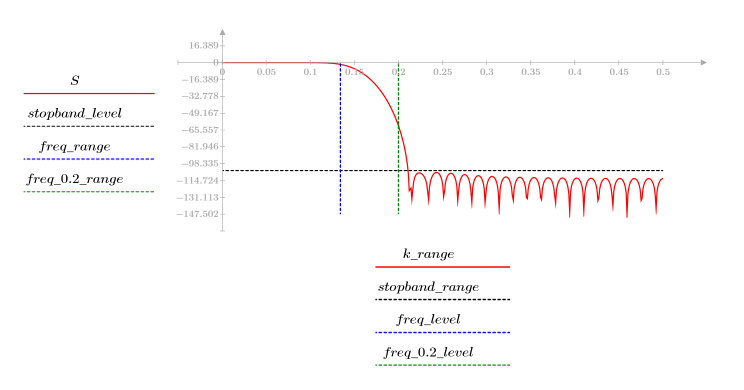
El rizado de la banda de supresión ronda los -105 dB.
Ventana rectangular de transición gradual
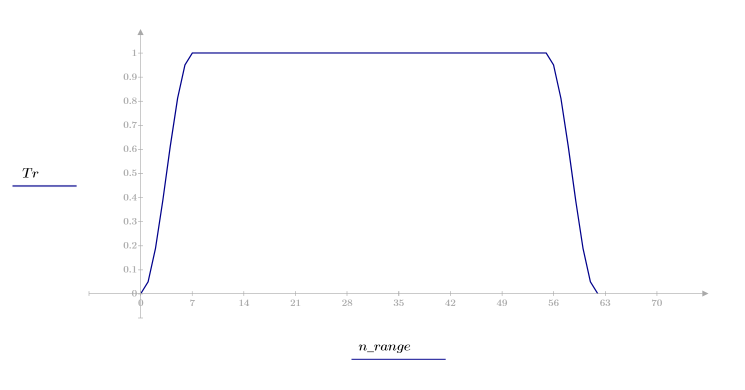
La función taprect devuelve la ventana rectangular de transición gradual de ancho N.
Esta ventana es horizontal en el medio, a la altura de 1, y presenta extremos redondeados con curvas de coseno. Los laterales derecho e izquierdo utilizan los valores:
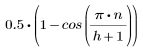
donde
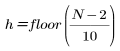
y n ejecuciones de 0 a h.
1. Aplique la función para filtrar por orden N y trazar el vector resultante.
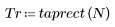
2. Calcule el impulso de respuesta en una ventana.
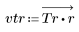
3. Utilice la función gain para calcular y trazar la ganancia en dB de este filtro, con coeficientes vtr, a una frecuencia de k/1000.
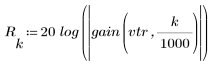
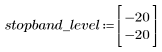
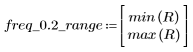
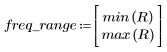
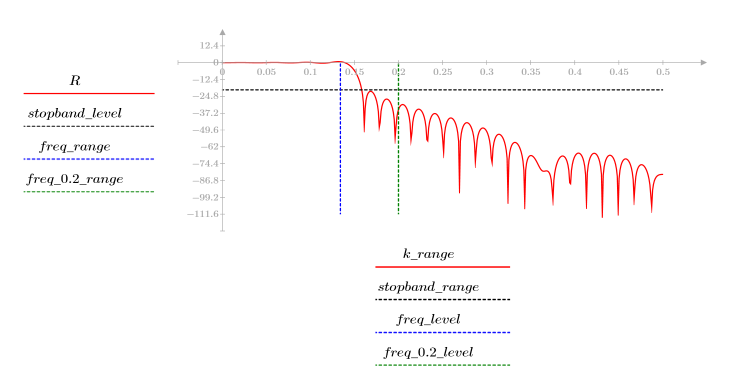
Ventana gaussiana
La función gaussian devuelve la ventana gaussiana de ancho N y el parámetro a. El número es un número real proporcional al inverso de la varianza gaussiana y debe cumplir el requisito 2 < a < 20.
El elemento k del vector resultante viene dado por:
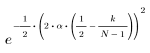
1. Aplique la función para filtrar por orden N y trazar el vector resultante.
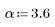
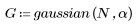
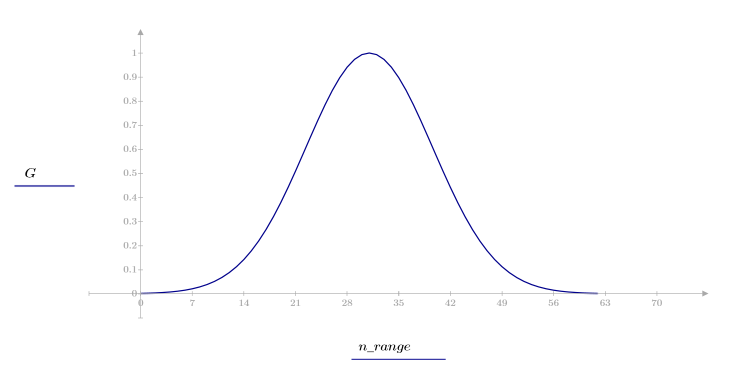
2. Calcule el impulso de respuesta en una ventana.
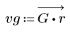
3. Utilice la función gain para calcular y trazar la ganancia en dB de este filtro, con coeficientes vg, a una frecuencia de k/1000.
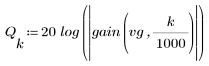
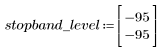
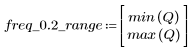
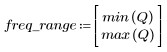
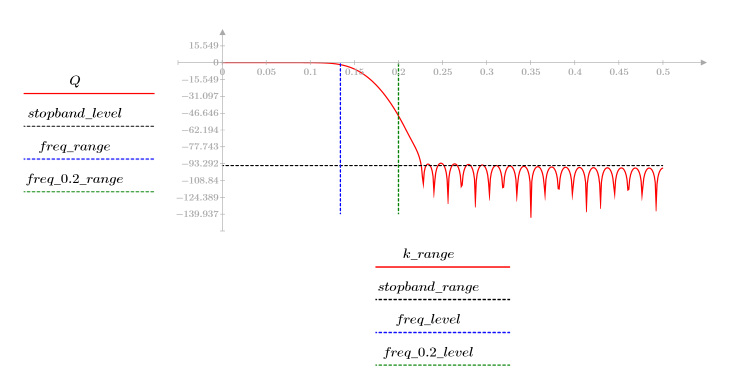
El rizado de la banda de supresión ronda los -95 dB.
Ventana de Kaiser
La función kaiser devuelve una ventana de Kaiser de ancho N y el parámetro b. El parámetro b debe cumplir el requisito 2≤b≤20.
El elemento k del vector resultante viene dado por:
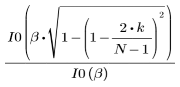
1. Aplique la función para filtrar por orden N y trazar el vector resultante.
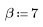
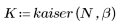
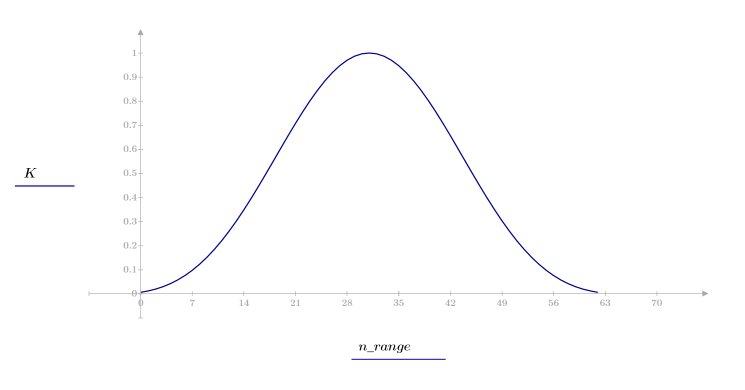
2. Calcule el impulso de respuesta en una ventana.
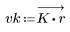
3. Utilice la función gain para calcular y trazar la ganancia en dB de este filtro, con coeficientes vk, a una frecuencia de k/1000.
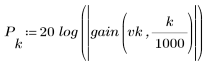
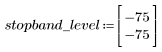
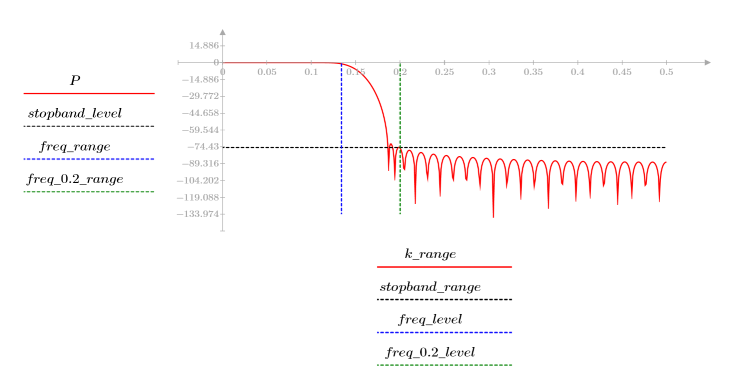
El rizado de la banda de supresión ronda los -75 dB.
Ventana de Chebyshev
La función cheby devuelve la ventana de Chebyshev o de rizado uniforme de ancho N y el parámetro b. El parámetro b especifica el rizado máximo del lóbulo lateral en dB y debe cumplir el requisito 1 < b; normalmente, b es > 50. La longitud de esta ventana debe ser impar. La ventana de Chebyshev se calcula tomando la transformada de Fourier discreta inversa de un polinomio de Chebyshev evaluado en puntos alrededor del círculo unidad. Consulte la publicación Programs for Digital Signal Processing (IEEE Press) para obtener más información sobre esta ventana.
1. Aplique la función para filtrar por orden N y trazar el vector resultante.
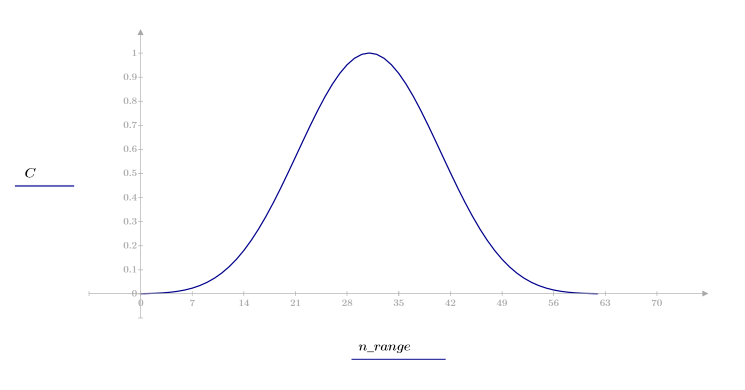
2. Calcule el impulso de respuesta en una ventana.
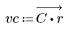
3. Utilice la función gain para calcular y trazar la ganancia en dB de este filtro, con coeficientes vc, a una frecuencia de k/1000.
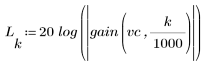
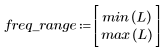
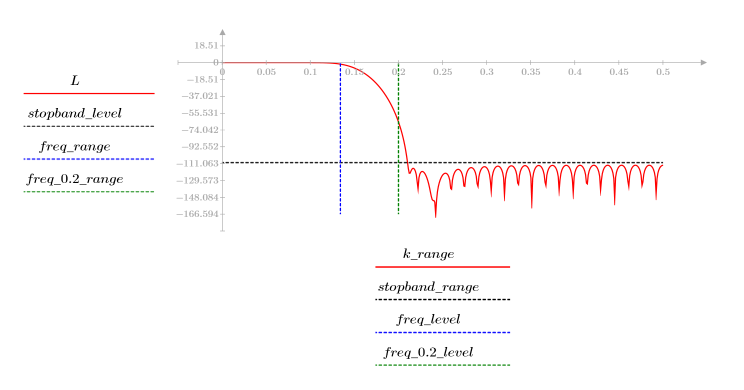
El rizado de la banda de supresión ronda los -110 dB.
Ventana de conicidad de coseno
La función costaper se parece a la función taprect en que devuelve una ventana rectangular con colas redondeadas que siguen una curva de coseno. Sin embargo, se puede utilizar el parámetro a para especificar el porcentaje de la ventana que se debería crear con una curva de coseno. El parámetro a se debe encontrar entre 0 y 1; un valor de 0 devuelve una ventana rectangular, mientras que un valor de 1 devuelve una curva de coseno elevada.
Para la parte redondeada de la ventana, el valor del elemento k viene dado por:
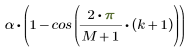
donde M es el número de elementos de la ventana que coinciden en una de las colas y viene dado por a-N:
1. Aplique la función para filtrar por orden N y trazar el vector resultante.
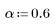
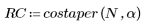
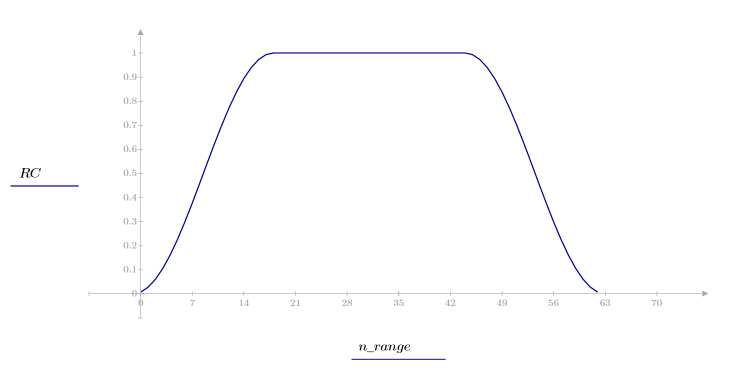
2. Calcule el impulso de respuesta en una ventana.
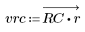
3. Utilice la función gain para calcular y trazar la ganancia en dB de este filtro, con coeficientes vrc, a una frecuencia de k/1000.
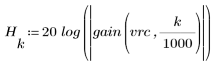
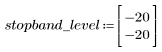
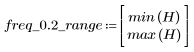
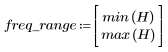
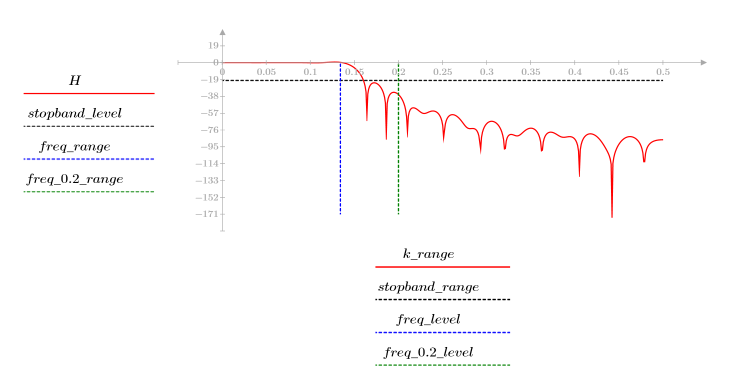
El rizado de la banda de supresión ronda los -20 dB.
Referencias
• S. Lawrence Marple, Jr., Digital Spectral Analysis with Applications, Prentice-Hall (1987).
• Lawrence R. Rabiner and Bernard Gold, Theory and Application of Digital Signal Processing, Prentice-Hall, Inc. (1975).
• T. W. Parks and C. S. Burrus, Digital Filter Design, Wiley-Interscience (1987).